4.2. Определение показания дифманометра (или дифпьезометра) скоростной трубки

Для выполнения задания достаточно уравнения Бернулли для осевой трубки:

где расстояние от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости;

р – давления в сечениях А-А и В-В соответственно;

– плотность циркулирующей жидкости;

g – ускорение свободного падения;

скорость течения жидкости в сечении А-А и В-В соответственно;

коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;

потери напора на участках между выбранными сечениями.

Пренебрегаем очень небольшими на малой длине между сечениями А-А и В-В потерями напора (hА-В = 0).

, если выбираем ось трубопровода за начало.

, так как жидкость внутри дифманометра почти неподвижна.

(для практических расчетов).

В итоге имеем: (4.17.)

Из рисунка видно разность давлений:

В результате уравнение 4.21. примет вид:

Имеем расчетную формулу для определения показания дифманометра:

Вариант	Значение ∆h, м
14	0,0542

4.3. Построение эпюр скоростей для сечения в месте установки скоростной трубки

Анализируя схему циркуляционной установки можно сделать вывод, что расход жидкости постоянный в любом сечении трубопровода. Следовательно, режим течения жидкости зависит от диаметра трубопровода на рассматриваемом участке. Это, в свою очередь, говорит об идентичности режима течения на участках трубопровода с одинаковыми диаметрами. В месте установки скоростной трубки режим течения идентичен режиму течения на участке трубопровода всасывающей линии. Следовательно, мы имеем турбулентный режим течения, который происходит в зоне сопротивления шероховатых труб.

Формула для распределения скоростей в круглой трубе при турбулентном режиме в зоне шероховатых труб имеет следующий вид:

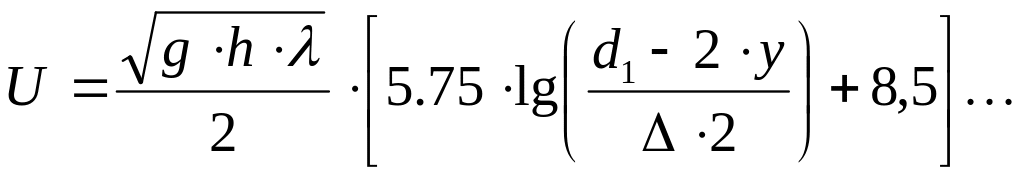
где местная скорость в данной точке сечения (м/с),

диаметр трубопровода (м),

расстояние от оси трубопровода (м),

эквивалентная шероховатость стенок труб (м),

показание дифманометра скоростной трубки.

Для построения эпюры скоростей зададим значения в интервале от 0 до с шагом 3,75 мм. Вычислим для каждого значения местную скорость. По результатам составим таблицу и построим график.

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

(м/с)

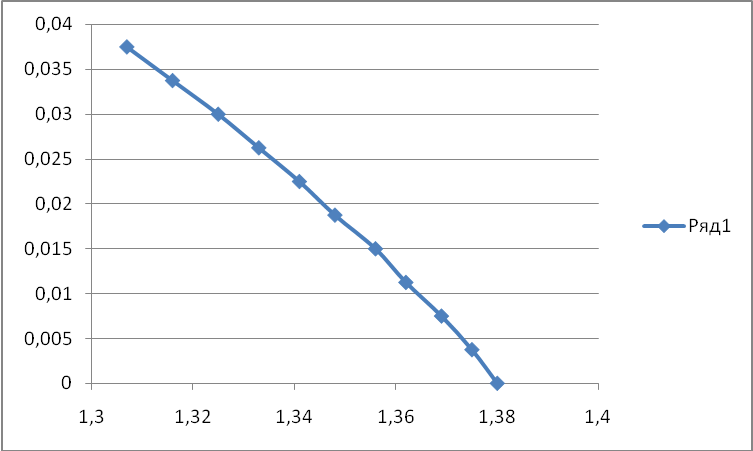
у, мм	0	3,75	7,5	11,25	15	18,75	22,5	26,25	30	33,75	37,5
,м/с	1,38	1,375	1,369	1,362	1,356	1,348	1,341	1,333	1,325	1,316	1,307

4.4. Определение показаний ртутного дифманометра расходомера вентури

Запишем уравнение Бернулли двух сечение 1-1 и 2-2:

(4.18)

где расстояние от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

р – давления в сечениях А-А и В-В соответственно (Па);

– плотность циркулирующей жидкости (кг/м3);

g – ускорение свободного падения (м2/с);

скорость течения жидкости в сечении А-А и В-В соответственно (м/с);

коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно.

потери напора на участках между выбранными сечениями.

Выберем ось трубопровода за начало отсчета, тогда , т.к. трубопровод горизонтален. Предположим, что по трубопроводу течет идеальная жидкость, что позволяет не учитывать потери напора .

(для практических расчетов).

Запишем (4.18) с учетом всех утверждений:

(4.19)

Т.к. расход в сечениях постоянен, то (4.20)

Подставим (4.20) в (4.19):

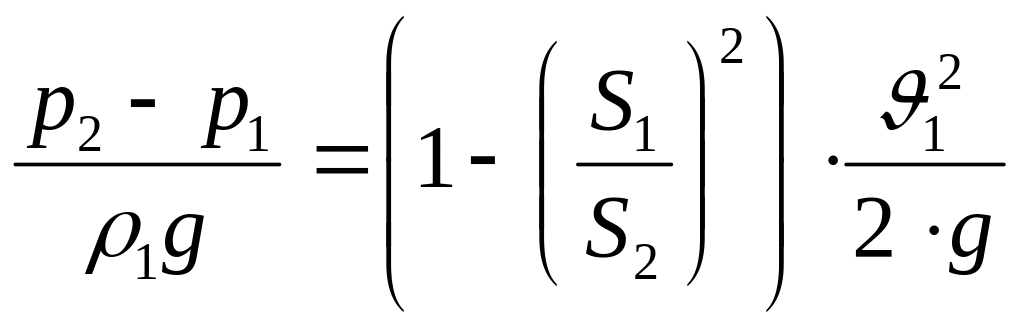(4.21)

В действительности расход меньше теоретического на безразмерный коэффициент , тогда с учетом потерь напора равна:

Разность давлений, измеренная дифманометром, определяется из следующего соотношения:

, где плотность ртути (кг/м3).

С другой стороны, разность давлений в сечениях 1-1 и 2-2 расходомера определяется при помощи дифманометра, обычно ртутного, где .

(4.22)

Приравниваем правые части уравнений (4.19) и (4.21):

;

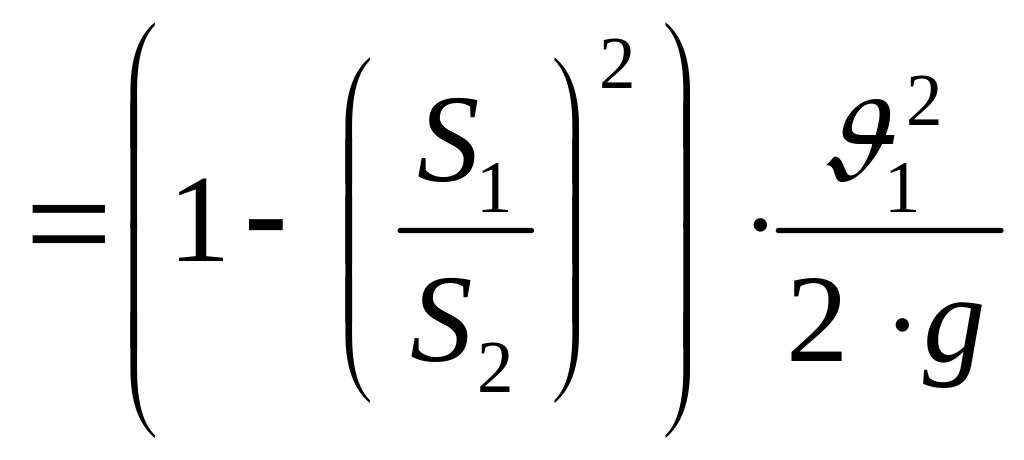Учитывая

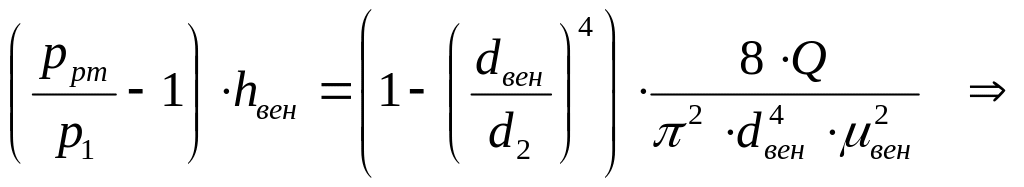
(4.23)

Вариант	Значение Нвен, м
14	9,39