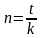Погашення єдиним платежем

Погашення боргу єдиним платежем розраховується за методом простих і складних відсотків.

Під нарощеною сумою кредиту розуміють початкову її суму з нарахованими процентами до кінця року.

Нарощена сума визначається множенням початкової суми кредиту на множник нарощення, який показує, у скільки разів нарощена сума більше початкової. Розрахункова формула залежить від виду процентної ставки, яка використовується, і умов нарощення.

Формула нарощення за простими процентами (або формула простих процентів):

S=P (1+ni)	(1)
де P – початкова сума кредиту; S – нарощена сума; і – ставка нарощення (десятковий дріб); n – строк кредиту, в роках.

При нарощенні простих процентів останні зростають в арифметичній прогресії. Ця величина визначається за формулою (2):

	(2)
де P – початкова сума кредиту; і – ставка нарощення (десятковий дріб); n – строк кредиту, в роках.

При використанні простих процентів строк, як правило, визначається у роках, також може бути в місяцях, днях. Якщо проценти розраховуються за точну кількість днів, то строк кредиту у формулі (1) визначається формулою (3):

	(3)
де t – кількість днів кредиту; к – кількість днів у році, або часова база (timebasis).

При цьому використовуються такі методи визначення кількості днів:

• метод «факт/факт» передбачає, що для розрахунку використовується фактична кількість днів у місяці та році;

• метод «факт/360» – для розрахунку використовується фактична кількість днів у місяці, але умовно в році 360 днів;

• метод «30/360» – для розрахунку використовується умовна кількість днів у році – 360, у місяці – 30.

У цьому випадку формула простих процентів буде представлена як:

	(4)
де S – нарощена сума; P – початкова сума кредиту; і – ставка нарощення (десятковий дріб); t – кількість днів кредиту; к – кількість днів у році, або часова база (timebasis).

Якщо процентна ставка не постійна, а змінюється у часі, то необхідно застосовувати формулу (5)

	(5)
де np – строк кредиту у періоді р; ip – ставка процентів у періоді р.

Формула нарощення за складними процентами (формула складних процентів):

	(6)
де P – початкова сума кредиту; S – нарощена сума; і – ставка нарощення (десятковий дріб); n – кількість періодів нарахування процентів.

Ануїтетна схема погашення кредиту

Ануїтет – це рівні один одному грошові платежі, які сплачуються через певні проміжки часу в рахунок погашення отриманого кредиту та відсотків за ним».

Аннуїтетна схема погашення кредиту – передбачає виплату банку рівних сум щомісячно, не залежно від заборгованості по тілу кредиту. Ця сума складається з частини погашення тіла кредиту та відсотоків за користування кредитом. Такий механізм має сенс при тривалому кредитуванні, оскільки є ймовірність, що частину суми буде погашено завдяки інфляції.

Основу всіх формул розрахунку кредиту з ануїтетними платежами становить так званий ануїтетний коефіцієнт. На його основі в подальшому знаходяться всі інші параметри кредиту. Формула розрахунку ануїтетного коефіцієнта:

	(7)
де К – коефіцієнт ануїтету; і – процентна ставка за один період нарахування платежів за кредитом; n – кількість періодів нарахування процентів.

Як правило, нарахування ануїтет них платежів за кредитом відбувається кілька разів на рік (в основному щомісячно, 12 разів на рік), а процентна ставка за кредитом дається у річному вимірі (річна процентна ставка). Тоді формула (7) має наступний вигляд:

	(8)
де ka – коефіцієнт ануїтету; і – річна процентна ставка за кредитом; n – кількість років кредитування; m – кількість разів нарахування платежів за кредитом в рік.

Далі розраховується щомісячний ануїтетний платіж за формулою (9):

	(9)
де А – щомісячний ануїтетний платіж за кредитом; ka – коефіцієнт ануїтету; Р – початкова сума кредиту.

Для побудови графіка платежів за ануїтетною схемою кредитування необхідно розрахувати щомісячні проценти, які будуть нараховуватися за кредитом. Для цього застосовують формулу (10):

	(10)
де Іt – процентний платіж за кредитом у періоді t; Pt – залишок основного боргу (тіла кредиту) за кредитом у періоді t; і – річна процентна ставка за кредитом; m – кількість разів нарахування платежів за кредитом в рік.

Крім того, щомісячні платежі за кредитом включають періодичне погашення самого тіла кредиту:

	(11)
де СРt – величина погашення основної суми боргу (тіла кредиту) у періоді t; Іt – процентний платіж за кредитом у періоді t; А – щомісячний ануїтетний платіж за кредитом.

Таким чином, повна вартість кредиту за весь період буде розраховуватися за формулою (12):

	(12)
де S – нарощена сума кредиту (повна вартість кредиту на кінець періоду); А – щомісячний ануїтетний платіж за кредитом; n – період кредитування (у роках); m – кількість разів нарахування платежів за кредитом в рік.