11 Клас Завдання для тематичного оцінювання № 1 по темі: «Границя і неперервність функції. Похідна»
1.
Вкажіть, який із числових проміжків є
розв’язком нерівності
.
а) [0;6]; в) (-6;6);
б) (-6;0); г) [-6;6].
2.
Вкажіть, який із числових проміжків є
розв’язком нерівності
.
а) [-4;4]; в) (-4;4);
б) (0;4]; г) (-4;0).
3. Яка з рівностей правильна?
а)
; в)
;
б)
; г)
.
4. Яка з рівностей правильна?
а)
; в)
;
б)
; г)
.
5.
Яке з чисел є границею функції
,
коли
?
а) 3; в) 36;
б) 4; г) 16.
6.
Яке з чисел є границею функції
,
коли
?
а) 4,5; в) 5;
б) 8; г) 6.
7.
Зразок обчислення похідної:
;
.
У якому випадку правильно знайдено
похідну функції
?
а)
; в)
;
б)
; г)
.
8.
Зразок обчислення похідної:
;
.
У якому випадку правильно знайдено
похідну функції
?
а)
; в)
;
б)
; г)
.
9.
Знайдіть похідну функції
а)
; в)
;
б)
; г)
.
10.
Знайдіть похідну функції
.
а)
; в)
;
б)
; г)
.
11.
Знайдіть похідну функції
.
а)
; в)
;
б)
; г)
.
12.
Обчисліть похідну функції
в точці
.
а) 4; в) 2;
б) 6; г) 0.
Завдання для тематичного оцінювання № 2 по темі: «Похідна та її застосування»
1.
Якщо
,
то функція
спадає на проміжку:
а)
; в)
;
б)
; г)
.
2.
Якщо
,
то функція
зростає на проміжку
а)
; в)
;
б)
; г)
.
3.
Якщо
,
то критичними точками для функції
є точки:
а) 10 і 0; в) 10 і -10;
б) -10 і 0; г) 100 і -100.
4.
Якщо
,
то критичними точками для функції
є точки:
а) -1; в) 0;
б) 1; г) 10.
5. Назвіть критичні точки функції, зображеної на графіку.
а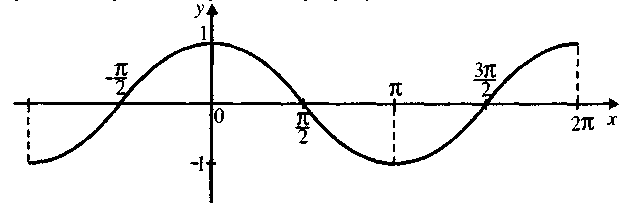
)
;
б)
;
в)
;
г)
.
6. Назвіть точки екстремуму функції, зображеної на графіку.
а)
; в)
;
б)
; г)
.
7. Знайдіть проміжки зростання функції, зображеної на графіку.
а)
; в)
;
б)
; г)
.
8. Назвіть найбільше значення функції, зображеної на графіку.
а) 1; в) ;
б)
; г)
.
9. Назвіть проміжки, на яких функція, зображена на графіку, набуває додатних значень.
а)
; в)
;
б)
; г)
.
10.
Якщо
,
то похідна функції в точці
дорівнює:
а)
-1; в)
;
б)
1; г)
.
11.
Знайдіть найбільше значення функції
на проміжку
.
а) -1; в) 0;
б) 1; г) 5.
12. Знайдіть найменше значення функції на проміжку .
а) -1; в) 0;
б) 1; г) 5.
Завдання для тематичного оцінювання № 3 по темі: «Інтеграл та його застосування»
Яка з функцій є первісною для функції
?
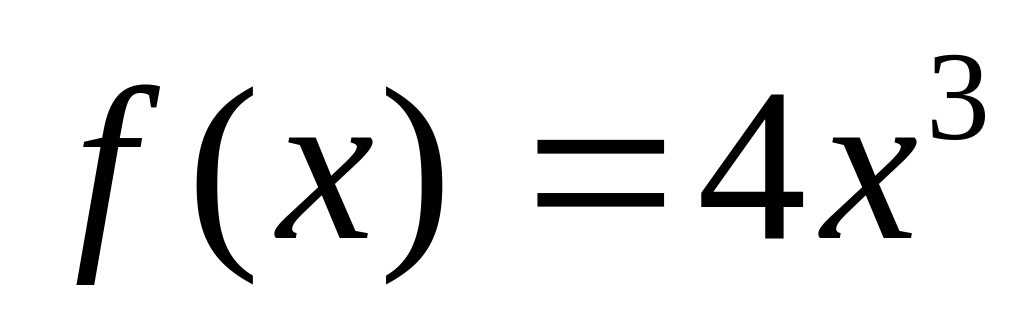а)
; б)
;
в)
; в)
.
Яка з функцій є первісною для функції
?
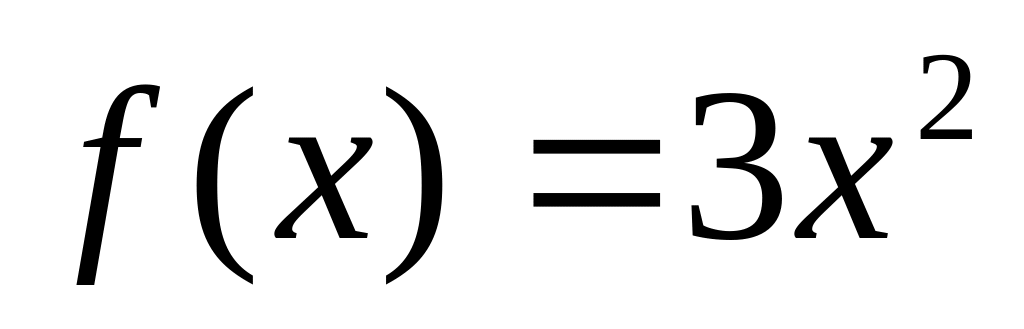а)
; б)
;
в)
; в)
.
3.
Яка з функцій є такою, що
?
а)
; б)
;
в)
; г)
.
4.
Яка з функцій є такою, що
?
а)
; б)
;
в)
; г)
.
5.
Укажіть для функції
первісну, графік якої проходить через
точку М(0;1)?
а)
; в)
;
б)
; г)
.
6. Яку з фігур, зображених на малюнку, можна назвати криволінійною трапецією?
а) 1; в) 3;
б) 2; г) 4.
1 2 3 4
7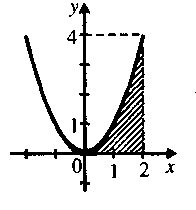
.
Якими лініями обмежена фігура, зображена
на рисунку?
а)
;
б)
;
в)
;
г)
.
8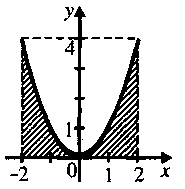
.
Якими лініями обмежена фігура, зображена
на рисунку?
а)
;
б)
;
в)
;
г)
.
9.
Укажіть вираз для обчислення площі
криволінійної трапеції, яку зображено
на рисунку, враховуючи, що
:
а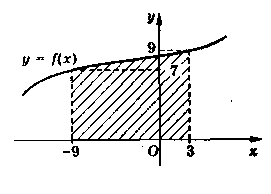
)
;
б)
;
в)
;
г)
.
10.
Обчисліть інтеграл
.
а) 4; в) 16;
б) 8; г) -4.
11.
Обчисліть інтеграл
.
а) 1; в) -1;
б) 0; г) -2.
12.
Обчисліть інтеграл
.
а)
; в)
1;
б)
; г)
-3.