18. Дисперсия и среднее квадратическое отклонение

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания .

Дисперсия характеризует меру рассеяния случайной величины вокруг математического ожидания. Недостатком дисперсии является то, что она имеет размерность квадрата случайной величины и её неудобно использовать для характеристики разброса.

Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое представляет собой квадратный корень из дисперсии .

Основные свойства дисперсии.

1. Дисперсия постоянной величины равна нулю, .

Доказательство: .

2. Постоянный множитель случайной величины можно выносить за знак дисперсии, предварительно возведя его в квадрат .

Доказательство. По свойствам математического ожидания

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин .

Доказательство. Используя определение дисперсии и свойство математического ожидания , дисперсию случайной величины можно выразить следующим образом: . Представим выражение в скобках в виде двучлена и запишем квадрат его суммы. Используя свойства математического ожидания суммы и произведения двух независимых случайных величин, получаем .

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, .

Доказательство. На основании свойства 3 можно записать .

5. Дисперсия случайной величины Х, равна разности между математическим ожиданием квадрата случайной величины Х и квадратом её математического ожидания, .

Доказательство. Используя определение дисперсии и свойства математического ожидания, имеем .

Пример 23. Найти дисперсию для распределения непрерывной случайной величины, заданной в примере 21.

Решение. В примере 21 было найдено математическое ожидание . Для нахождения дисперсии используем её 5 свойство. Вычислим . Тогда дисперсия равна .

xi	0	1	2	3
pi	0,1	0,3	0,4	0,2

Пример 24. Найти дисперсию и среднее квадратическое отклонение для дискретной случайной величины, имеющей ряд распределения

Решение. Математическое ожидание для этого распределения найдено в примере 22, и оно равно . Для нахождения дисперсии вычислим . Тогда дисперсия равна . Среднее квадратическое отклонение найдём по формуле .

Пример 25. Дискретная случайная величина Х имеет только два возможных значения: х₁ и х₂, причём х₁<х₂. Вероятность того, что Х примет значение х₁, равна 0,5. Найти закон распределения Х, зная математическое ожидание и .

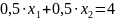Решение: По условию нормировки имеем , отсюда . Так как , то или . По пятому свойству дисперсии , тогда , или . Подставив в полученное уравнение , получим или . Решая полученное квадратное уравнение, находим и и, По условию задачи , следовательно: х₁=3

xi	3	5
pi	0,5	0,5

и , и искомый закон распределения имеет вид