7. Формула полной вероятности

Т. Если событие А может наступить только при условии появления одного из событий H₁, H₂, …. H_n , образующих полную группу несовместных событий, то вероятность события А равна сумме произведений вероятностей каждого из событий H₁, H₂, …. H_n на соответствующую условную вероятность события А,

Это формула полной вероятности, а события H₁, H₂, …. H_n, - гипотезами, причём сумма вероятностей гипотез равна единице, то есть

Доказательство. Формулу полной вероятности можно вывести на основании теорем умножения и сложения вероятностей. Согласно условию, событие А можно представить в виде суммы несовместных событий . По теореме сложения вероятностей несовместных событий можно записать , применяя теорему умножения к каждому слагаемому получаем или

Примечание. Формула полной вероятности используется до совершения события.

Пример 11. Три завода производят одинаковые изделия, которые поступают на один склад, причём первый завод производит 30%, второй 20% и третий 50% всех поступивших на склад деталей. Процент брака для первого завода 5%, для второго 8% и для третьего 10%. Найти вероятность того, что наудачу взятая со склада деталь окажется браковочной.

Решение. Обозначим события: А - деталь бракованная, так как вероятность этого события зависит от того, на каком заводе она произведена, то добавим следующие гипотезы: Н₁- деталь произведена на первом заводе, Н₂- на втором заводе, Н₃ - а третьем заводе. По условию задачи ; ; и ; ; . Тогда искомая вероятность по формуле полной вероятности равна

8. Формула Байеса

Формула Байеса применяется при решении практических задач, когда событие А, появляющееся совместно с каким-либо из событий H₁, H₂, …. H_n которые образуют полную группу несовместных событий (гипотез), произошло и требуется произвести количественную переоценку вероятностей событий H₁, H₂, …. H_n. Априорные (до опыта) вероятности известны. Требуется вычислить апостериорные (после опыта), вероятности, то есть, нужно найти условные вероятности .

Пусть событие А может наступить при условии появления одной из гипотез H₁, H₂, …. H_n. Вероятность совместного появления события А с одной из гипотез Н_m по теореме умножения равна ,

Отсюда или

Полученные формулы носят название формулы Байеса.

Пример 12. В первой группе 20, во второй 25, в третьей группе 15 студентов. Вероятность сдать экзамен на отлично для студентов первой группы равна 0,6, для студентов второй – 0,3, для третьей – 0,4. Наудачу взятый студент сдал экзамен на отлично. Найти вероятность того, что он из третьей группы.

Решение. Обозначим события: А - наудачу взятый студент сдал экзамен на отлично, Н₁ – студент из первой группы, Н₂ – студент из второй группы, Н₃ – студент из третьей группы. По условию задачи ; ; ; ; ; 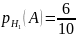. Тогда искомая вероятность по формуле Байеса равна = .

9. Схема независимых испытаний.

Формула Бернулли

На практике приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие А. При этом представляет интерес не исход каждого отдельного испытания, а общее число появлений события А в результате определённого количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа m появлений события А в результате n испытаний. Рассмотрим случай независимых испытаний.

Испытания называются независимыми, если результат одного испытания не зависит от результатов других испытаний и вероятность появления события А в каждом испытании постоянна.

Пусть происходит n независимых испытаний, в каждом из которых событие А может либо появиться с вероятностью р, либо не появиться с вероятностью 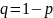Рассмотрим событие В_m , состоящее в том, что событие А в этих n испытаниях появилось ровно m раз и, следовательно, не появилось m-n раз. Обозначим через 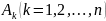появление события А, через - не появление события А в k-м испытании. По условию имеем и .

Событие может появиться m раз в различных последовательностях или комбинациях, чередуясь с противоположным событием . Число возможных комбинаций такого рода равно числу сочетаний из n элементов по m, то есть 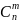. Следовательно, событие В_m можно представить в виде суммы различных комбинаций, несовместных между собой, причём число слагаемых равно . Где в каждое слагаемое событие А входит m раз, а событие входит раз. Вероятность каждой последовательности по теореме умножения равна . Так как общее число таких последовательностей равно то, используя теорему сложения для несовместных событий, получим вероятность события В_m, равную или . Последняя носит название формулы Бернулли.

Пример 13. Найти вероятность того, что при пяти бросаниях монеты герб появится один раз.

Решение. Вероятность появления герба при одном бросании монеты равна , вероятность его не появления . Тогда вероятность появления одного герба при пяти бросаниях по формуле Бернулли равна .
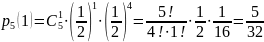