40. Оценка математического ожидания и дисперсии

Наиболее важными числовыми характеристиками случайной величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают математическое ожидание и дисперсию.

Т.1. Средняя арифметическая , вычисленная по п независимым наблюдениям над случайной величиной Х, которая имеет математическое ожидание , является несмещённой оценкой этого параметра.

Доказательство. Пусть независимые наблюдения над случайной величиной. По определению . Найдём . Следовательно: .

Т.2. Средняя арифметическая , вычисленная по п независимым наблюдениям над случайной величиной, которая имеет математическое ожидание и дисперсию , является состоятельной оценкой этого параметра.

Доказательство. Вычислим: . Запишем неравенство Чебышева для средней арифметической , или . При достаточно большом числе испытаний величина является числом, близким к нулю. Поэтому для сколь угодно малого числа выполняется неравенство , определяющее свойство состоятельности выборочных оценок.

Получение эффективных оценок - сложное дело. Приведём без доказательства важный для практики факт. Если случайная величина Х распределена по нормальному закону с параметрами , то несмещённая оценка математического ожидания имеет минимальную дисперсию , поэтому средняя арифметическая в этом случае является эффективной оценкой математического ожидания .

Т.3. Если случайная выборка состоит из п независимых наблюдений над случайной величиной Х с математическим ожиданием и дисперсией , то выборочная дисперсия не является несмещённой оценкой генеральной дисперсии.

Доказательство. По условию и тогда . Упростим выражение , подставив полученное в выражение для эмпирической дисперсии получим 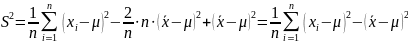. Но так как и то . То есть является смещённой оценкой дисперсии генеральной совокупности.

Несмещённой оценкой дисперсии генеральной совокупности является . Обычно эту оценку называют исправленной выборочной дисперсией. Дробь называют поправкой Бесселя. Тогда имеем равенство . При малых значениях п поправка Бесселя довольно сильно отличается от единицы, с увеличением п она быстро стремится к единице. При практически нет разницы между и . Можно показать, что оценки и являются состоятельными оценками .

Несмещённой, состоятельной и эффективной оценкой является оценка , для вычисления которой необходимо знать математическое ожидание. Заметим, что оценка эффективна лишь при условии нормальности распределения случайной величины Х в генеральной совокупности. Оценки и не являются эффективными. В том случае, когда значение математического ожидания неизвестно, то для оценки дисперсии используют состоятельную и несмещённую оценку .

41. Метод максимального правдоподобия

Основным способом получения оценок параметров генеральной совокупности по данным выборке является метод максимального правдоподобия. Основная идея метода заключается в следующем.

Пусть - результаты независимых наблюдений над случайной величиной Х, которая может быть как дискретной, так и непрерывной; - вероятность значения (если случайная величина дискретна) и плотность вероятности (если случайная величина непрерывна). Функция зависит от неизвестного параметра , который требуется оценить по выборке.

Если - независимые случайные величины, то функцией правдоподобия называется выражение . В качестве оценки неизвестного параметра берется такое значение , при подстановке которого вместо параметра получаем максимальное значение функции . Оценку обычно называют оценкой максимального правдоподобия. Оценка зависит от количества и числовых значений случайных величин , следовательно, сама является случайной величиной.

При максимизации функции подразумевается, что значения фиксированы, а переменной является параметр (иными словами, максимум отыскивается в предположении, что заменены их числовыми значениями). Если дифференцируема относительно параметра , то для отыскания максимума надо решить уравнение . В качестве оценки выбрать решение, которое обращает функцию в максимум. Иногда удобно рассматривать уравнение .

Согласно методу максимального правдоподобия для нормально распределенной генеральной совокупности в качестве оценок математического ожидания и дисперсии нужно брать соответственно среднюю арифметическую и эмпирическую дисперсию .

Пример 40. Найти методом максимального правдоподобия по выборке точечную оценку неизвестного параметра показательного распределения, плотность которого .

Решение. Составим функцию правдоподобия . Найдём логарифмическую функцию правдоподобия . Найдём первую производную по . Отсюда . Так как в силу положительности то оценкой метода максимального правдоподобия параметра является величина, обратная среднему арифметическому.