29. Вариационные ряды

Генеральной совокупностью называется совокупность всех мыслимых наблюдений, которые могли бы быть сделаны при данном реальном комплексе условий измерений. Число членов, образующих генеральную совокупность, называется объёмом генеральной совокупности.

Выборочной совокупностью или просто выборкой объёмом п называется совокупность п объектов, отобранных из исследуемой генеральной совокупности.

Вариантами называются различные значения признака, а варьированием – изменение значений признака.

Расположение наблюдаемых значений в порядке возрастания или убывания называется ранжированием выборки.

Если признак по своей сущности таков, что различные значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующийся признак.

Число, показывающее, сколько раз встречается вариант х в ряде наблюдений, называется частотой варианта m_x.

Вместо частоты варианта х можно рассматривать её отношение к общему числу наблюдений п, которое называется частостью варианта х и обозначается . Так как общее число наблюдений равно сумме частот всех вариантов , то справедлива следующая цепочка равенств: .

Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.

Наряду с понятием частоты используется понятие накопленной частоты, которую обозначают . Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений называют накопленной частостью и обозначают . Очевидно, что .

Признак называется непрерывно варьирующим, если он может принять любое значение в некотором числовом интервале.

По полученным данным такого признака трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число вариантов). Для получения ясной картины нужно объединить полученные значения в несколько интервалов.

Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.

Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.

Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. 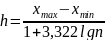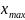Для определения оптимального интервала h, то есть такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса , где: и - соответственно максимальный и минимальный варианты. Величина характеризует число интервалов m, но так как количество интервалов целое число, то её округляют до целого значения. При этом желательно, чтобы было минимальным для возможных значений m. Длина интервала имеет ту же точность, что и варианты.

Пример 33. Найти оптимальную длину интервала по следующим данным, и , причём значения вариантов целые числа.

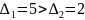Решение. Вычислим . Возможные количество интервалов 7 или 6. Соответствующие им длины интервалов равны . Тогда и . Так как , то для уменьшения погрешностей желательно взять шесть интервалов, имеющих длину 10.