3. Метод наименьших квадратов

Данный метод основан на определении зависимости удоя молока от расхода кормов, для этого необходимо составить систему уравнений, выявить математическую модель, с помощью которой можно описать зависимость удоя молока от расхода кормов. В начале рассчитаем необходимые коэффициенты (табл. 15). Для точности расчетов округление значений в табл. 15 необходимо осуществлять до десятитысячных.

Таблица 15 - Расчёт зависимости удоя молока от расхода кормов

Года	Расход кормов на 1ц молока (Хi), ц корм. ед.,	Удой молока на 1 корову (Уi), ц	Уi * Хi	Хi2	Хi3	Хi4	Хi2 * Уi
1
2
3
…
n

Для расчёта коэффициентов используются следующие системы уравнений:

1.

2.

Расчёт системы уравнений 1.

Преобразуем второе уравнение:

, отсюда

Подставляем это выражение в первое уравнение:

Раскрыть скобки и решить, сделать проверку полученных результатов.

Уравнение 1 примет вид:

Расчёт системы уравнений 2.

Из системы уравнений 2 составим матрицу вида , где:

m – количество строк;

n – количество столбцов.

Уравнение имеет вид:

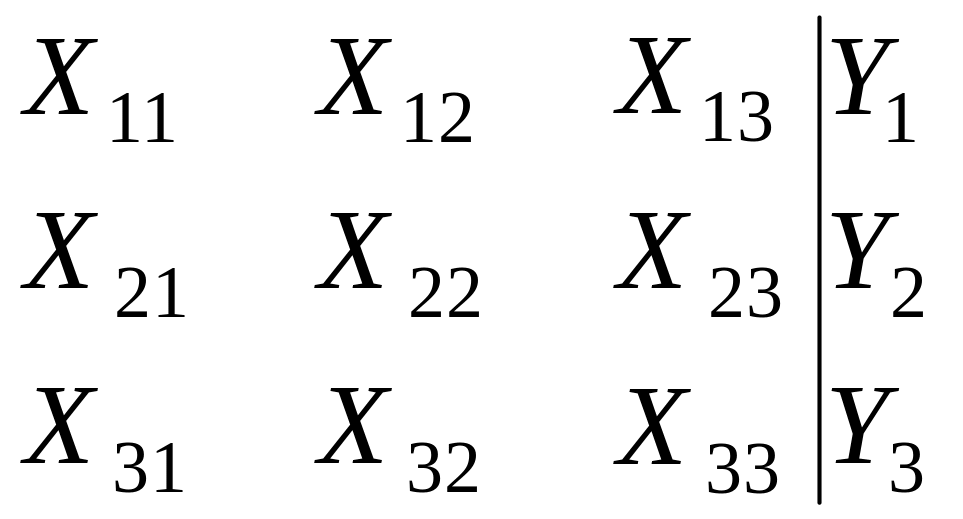
Решаем методом Крамара:

Вычисляем определитель матрицы (Δ):

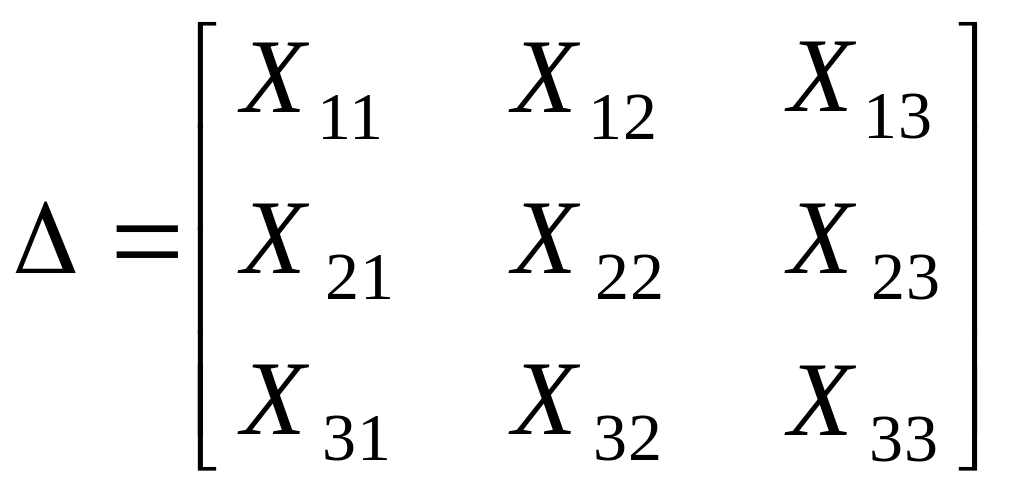
Определитель третьего порядка вычисляется:

1 СПОСОБ:

Для запоминания существует метод «звёздочка, треугольник»

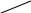
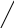
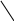
Δ = –

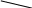
Если , то уравнение имеет решение.

; ;

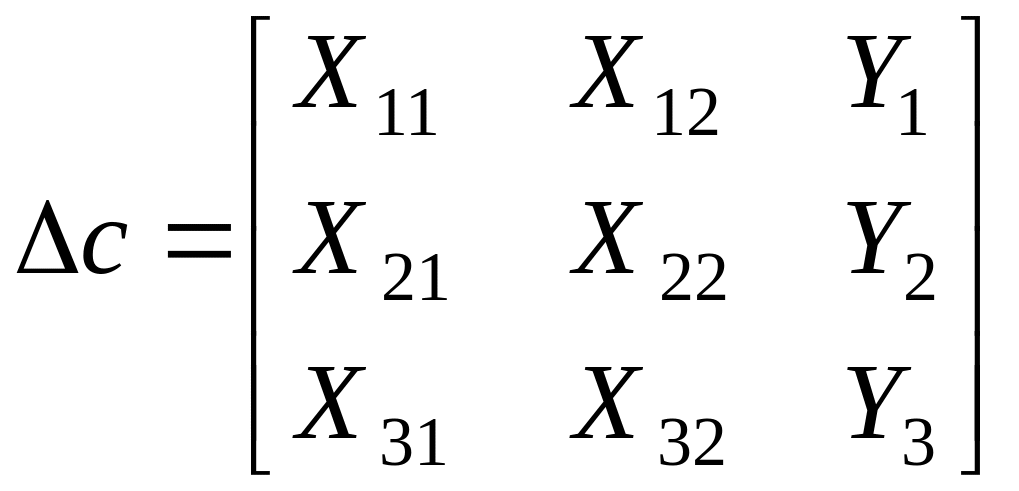
2 СПОСОБ:

Вычисление Δa, Δb и Δс по элементам ряда.

,

где Y₁, Y₂, Y₃ – алгебраическое дополнение, которое вычисляется по формуле:

,

где M_ij – минор соответствующего столбца и строки.

Δb и Δс определяется аналогично. Затем определяются коэффициенты а₂, b₂ и с произвести проверку полученных результатов.

В результате расчётов составим уравнение по определению средних уровней удоя молока на 1 корову, уравнение 2 примет вид:

Чтобы выбрать из двух полученных уравнений оптимальное, определим сумму квадратов отклонений расчётных средних удоев молока от фактических данных (табл. 16).

Таблица 16 - Расчёт отклонений расчётных уровней от фактических

№	Yi	Xi	Расчётные уровни по уравнению		Отклонения
					(графа2– графа4)2	(графа2– графа5)2
1	2	3	4	5	6	7
1
2
3
…
n

Находим наименьшую сумму квадратов отклонений при решении системы уравнений 1 и 2. Для дальнейших расчётов применим то уравнение где наименьшая сумма квадратов отклонений. Чтобы рассчитать прогнозный уровень продуктивности необходимо определить плановый расход кормов на 1 ц молока (Х_i), применив метод экстраполяции. Далее плановое значение Х_i подставляем в соответствующее уравнение:

или

Краткие выводы: