1.Основные свдения о методе имитационного моделирования

Различают полунатурное (натурное), тренажерное и математическое моделирования исследуемых систем и процессов. При этом элементы математического моделирования являются неприменными составляющими также полунатурного (натурного) и тренажерного моделирования.

Одним из разновидностей математического моделирования является имитационное моделирование, котрое может быть детерминированным, статитстическим или смешанным. Метод детерминированного имитационного омделирования применяеться для решения задач, в которых начальные данные, по которым необходимо вычислить конечный результат процесса, являются детерминированными, то есть неслучайными величинами. Такое моделирования, если оно осуществляеться с использованием электронной вычислительной машины (ЭВМ), называют также диалоговым режимом работы иследователя с ЭМВ. Например, нас может интересовать временная загруженность органа обслуживания воздушного движения (ОВД) при реализации разных вариантов плана полетов.Тогда, составив соответствующую программу, в ЭМВ вводят данные одного из вариантов плана,по которым она вычисляет и выдает исследователбю (операторы) соответствующий показатель, который характерезует упомянутую загруженность.

В рассмотернном выше процессе детерминированного имитационного моделированиякаждым вариантом плана полетов предполагается определенное время вылета каждого воздушного судна (ВС), а также пролета ним контрольных точек. Согласно статистическим данным, которые приводятся в литературных источниках, можно считать, что такие отклонения происходят в соответствии с нормальным законом распределения вероятности их значений, математическое ожидание которых равняется нулю, а среднее квадратичное отклонение составляет 6 – 8 минут. А случайные именения времени вылета ВС и пролета ними контрольных точек обуславливают случайные изменения показателя временной загруженности органа ОВД. Поэтому после определения наиболее рационального варианта плана полетов нас может интересовать, в каких границах будет изменяться или какое среднее значение будет иметь показатель загруженности органа ОВД при реалтзации такого плана и случайных изменениях запланированного времени вылета ВС (пролета ними контрольных точек). Теперь будем иметь задачу, в которой определяемый результат зависит от начальных случайных величин (упомянутого времени) и поэтому сам будет случайным.Такие задачи решаютметодом статистического моделирования, который также называют методом Монте-Карло. Посколько теперь конечный результат процесса (загруженности органа ОВД) принимает случайные значения, то для его оценки вычисляют статистические оценки числовых характеристик (параметров распределения) результирующей случайной величины. Как правило, ими являются статистические оценки математического ожидания (среднее арифметическое значение) и дисперсии случайной величины.

2.Последовательность решения задачи методом статистического моделирования

Как отмечалось выше, конечной целью статистического моделирования являеться вычисление статистических оценок числовых характеристик (параметров распределения) случайно величины, которая является результатом исследуемого процесса.Как правило, это оценки математического ожидания и дисперсии результирующей случайной величины. Если величины х₁, х₂, ... , х_n являются результатами n реализаций одного и того же процесса , то выборочные значения математического ожидания m и дисперсии σ² результирующей случайной величины вычисляются по формулам:

=

=

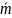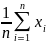
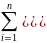
Значения оценок и ² достаточно близки к математическому ожиданию m и димперсии σ² результирующей случайной величины, если .

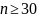В качестве примера рассмотрим последовательности решения следующей задачи.

Необходимо оценить точность выхода ВС из точки А в точку В (рис. 1) при условии, что полет выполняется по прямой в режиме счисления пути.

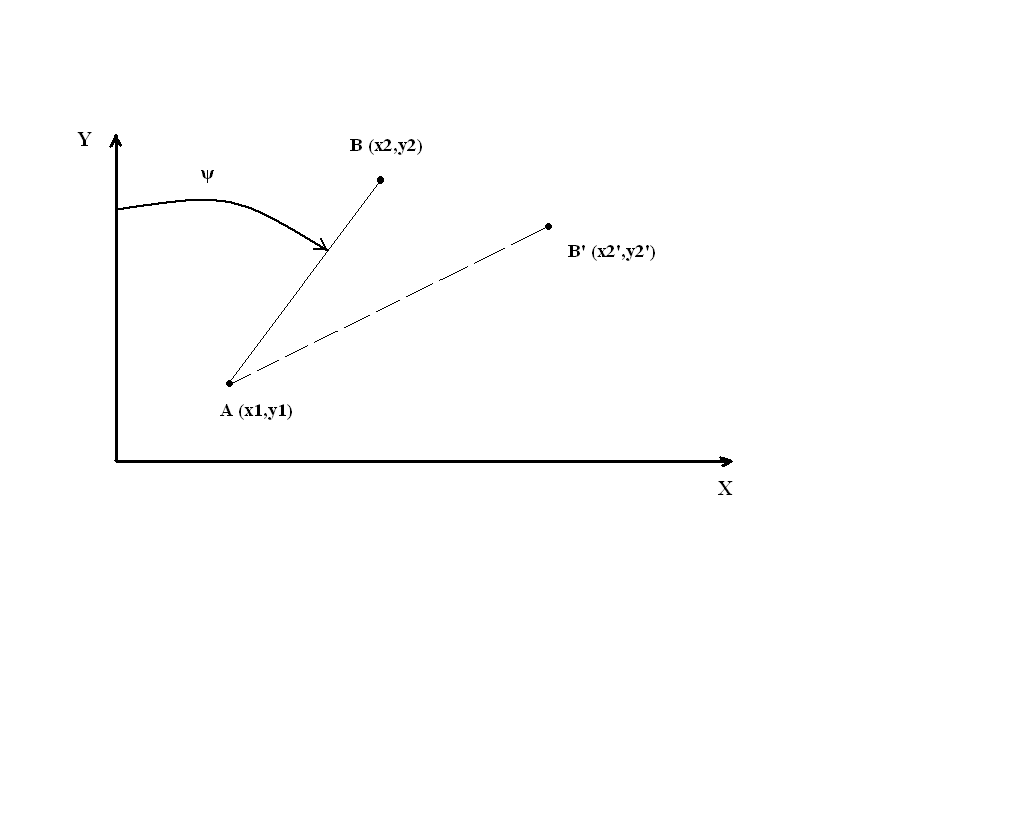
Рис. 1. Оценкка точности выхода ВС из исходной точки в расчетную.

С целью некоторого упрощения задачи сначала считаем, что такой оценки требует только точность по координате Х ортодромической системы координат ХОУ (оценка по координате У осуществляется аналогично). Считаем также, что отсчет курса 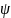полета осуществляется относительно оси ОУ.

Экипажу ВС известны курс полета , расстояние S между точками А и В, а также истинная скорость 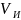с которой будет выполняться полет. Перед выполнением полета в режиме счисления пути экипаж определяет время полета: t=S/ . Чтобы выйти из точки А в точку В, экипаж в процессе выполнения полета выдерживает заданные (расчетные) значения курса и истиннной скорости на протяжении времени t. Но и курс, и скорость выдерживаються с существенными погрешностями, в результате чео ВС будет выведено, например в точку В' (считают, что отсчет времени осуществляется достаточно точно). 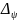Поскольку погрешности и 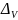выдерживание курса и скорости являются случайными величинами, то случайными будут также значения координат х'₂ и у'₂ точки В'.

Если не учитывать погрешности и , то

x₂=х₁+ t sin .

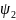В случае учета упомянутых погрешностей координат Х конечной точки точки полета будет иметь значение:

х'₂=x₁+( + )t sin ( + ).

( 1 )

Поэтому для решения задачи методом статического моделирования необходимо знать:

- аналитическое выражение, связывающее результирующую случайную величину ( в приведенном примере это х'₂ ) с исходными случайными величинами ( в примере это и ) , то есть выражение ( 1 );

- вероятностный закон распределения каждой исходной случаной величины и его параметры ( этими параметрами является, как правило, матиматическое ожидание и дисперсия).

Зная вероятностный закон распределения случайной величины и используя специальную литературу по вопросам статистического моделирования, определим форму алгоритма, по которому можно вычислить ("разыграть") случайные значения упомянутой величины.

В литературных источниках есть информация, в соответствии с которой погрешности и можно считать распределенными нормально с нулевым математическим ожиданием, а значения средних квадратических отклонени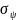й и 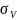( дисперси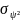й и 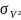) погрешностей и зависят от типа ВС. А "розыгрыш" нормально распределенной случайной величины х с нулевым математическим ожиданием можно осуществить по алгоритму ( существуют также другие формы алгоритмов для такого розыгрыша):

х=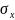 ( 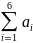- 3 ) ,

( 2 )

где: - среднее квадратичное значение случайной величины х;

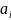- случайные числа, равно распределенные в диапазоне 0 – 1.

В специальной литературе по математической статистике проводятся таблицы случайных чисел, равномерно распределенных в диапазоне 0 – 1. Кроме того, любая ЭВМ и даже некоторые микрокалькуляторы вычмсляют ( 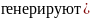такие числа в соответствии со стандартной подпрограммой.

Итак, теперь можем записать выражение ( 1) в такой форме:

х'₂=х₁+ t+t ( - 3 ) sin ,

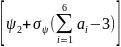( 3 )

где: и - средние квадратичные отклонения погрешностей выдерживания расчетных (заданных) значений истинной скорости и курса полета.

Случайное значение координат У конечной точки полета по прямолинейной траектории в режиме счисления пути:

у'₂=у₁+ t+t ( - 3 ) cos ,

( 4 )

Можно также показать, что в случае, если выход из точки с координатми х2, у2 в точку с координатами х3, у3 осуществляется с выполнением координированного разворота с радиусом R, то без учета погрешностей выдерживания заданной траектории:

x₃= х₂ + Rcos -Rcos ;

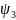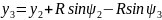, (5), (6)

где:

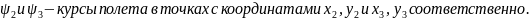
Падиус координированого разворота

,

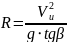где: g – ускорение свободного подения;

β – угол крена ВС в процессе выполнения разворота.

Заданое значение угла β выдерживается с существенным погрешностями,которые распределены нормально с нулевым математическим ожиданием и дисперсией 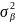, значение которой завсисит от типа ВС.

Тогда, учитывая погрешности 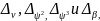выражения (5) и (6) запишем в такой форме:

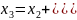-cos ,

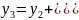
(7), (8)

Используя формулы можем «розыграть»случайеое значение координат конечной точки полета по прямолинейной или криволинейной траектории соответственно.