К онтрольні запитання

1. Дайте означення паралелепіпеда.

2. Назвіть основні властивості граней і ребер паралелепіпеда.

3. Сформулюйте відомі вам властивості діагоналей паралелепіпеда.

4. Який паралелепіпед називається прямим?

5. Який паралелепіпед називається похилим?

6. Який паралелепіпед називається прямокутним? Що таке лінійні розміри прямокутного паралелепіпеда?

7. Яка фігура лежить в основі паралелепіпедів: прямого, похилого та прямокутного?

8. Якою фігурою є грані паралелепіпедів: прямого, похилого та прямокутного?

9. Дайте означення куба.

10. Назвіть основні властивості куба.

11. За якою формулою можна знайти площу основи довільного паралелепіпеда, прямокутного паралелепіпеда, куба?

12. Чому дорівнює площа бічної поверхні паралелепіпеда?

13. Чому дорівнює площа повної поверхні паралелепіпеда?

14. Чому дорівнює площа бічної та повної поверхні куба?

Тема: Розв’язування задач на властивості піраміди та знаходження площі її поверхні.

Мета заняття: формування вмінь розпізнавати і знаходити невідомі елементи піраміди і зрізаної піраміди та знаходження площ їх поверхонь.

ПІРАМІДА

Пірамідою називається многогранник, одна грань якого (основа) – многокутник, а всі решта граней (бічні) – трикутники, що мають спільну вершину (вершина піраміди).

Властивості:

1. Якщо всі бічні ребра піраміди рівні, то вони нахилені до площини основи під однаковими кутами і вершина цієї піраміди проектується у центр кола, описаного навколо основи піраміди.

2. Якщо всі бічні ребра піраміди нахилені до площини основи під однаковими кутами, то вони рівні.

3. Якщо всі бічні грані піраміди нахилені до площини основи під однаковими кутами ,то вершина піраміди проектується в центр кола, вписаного в основу піраміди, а площа основи дорівнює добутку площі бічної поверхні піраміди на косинус кута , тобто .

4. Якщо бічне ребро піраміди утворює рівні кути зі суміжними сторонами основи, то основа висоти піраміди знаходиться на бісектрисі кута, утвореного цими сторонами основи.

5. Якщо в деякій піраміді дві суміжні бічні грані перпендикулярні до основи, то спільне ребро цих граней є висотою піраміди.

6. Якщо тільки одна бічна грань піраміди перпендикулярна до площини основи, то висотою піраміди буде висота цієї грані.

Зрізаною пірамідою називається частина піраміди, що міститься між її основою і перерізом піраміди, паралельним основі.

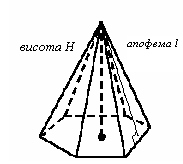
Рис. 11	ПРАВИЛЬНА ПІРАМІДА Піраміда називається правильною, якщо її основа - правильний многокутник, а вершина проектується в центр основи. Властивості: 1. Бічні грані – рівні між собою рівнобедрені трикутники. 2. Бічні ребра рівні між собою. 3. Апофеми рівні між собою (апофемою піраміди називається висота її бічної грані, проведена з вершини піраміди).
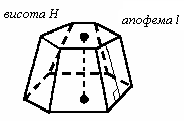
Рис. 12	ПРАВИЛЬНА ЗРІЗАНА ПІРАМІДА Властивості: Бічні грані – рівні між собою рівнобічні трапе-ції. 2. Бічні ребра рівні між собою. 3. Апофеми рівні між собою.

ПЛОЩА ПОВЕРХНІ ДОВІЛЬНОЇ ПІРАМІДИ
	Піраміда	Зрізана піраміда
Бічна поверхня	де Sі – площа однієї бічної грані	де Sі – площа однієї бічної грані
Повна поверхня	Sповн =Sбіч+Sосн	Sповн =Sбіч+S + s, де S – площа нижньої основи, s – площа верхньої основи

ПЛОЩА ПОВЕРХНІ ПРАВИЛЬНОЇ ПІРАМІДИ
	Піраміда	Зрізана піраміда
Бічна поверхня	де Р – периметр основи, l - апофема	де Р – периметр нижньої основи, р – периметр верхньої основи, l - апофема
Повна поверхня	Sповн =Sбіч+Sосн	Sповн =Sбіч+S + s, де S – площа нижньої основи, s – площа верхньої основи

Р ОЗГЛЯНЕМО ПРИКЛАДИ

Задача №1

Доведіть, що бічна поверхня піраміди, в якій усі двогранні кути при основі рівні, дорівнює відношенню площі основи піраміди до косинуса лінійного кута двогранного кута на основі піраміди.

Доведення

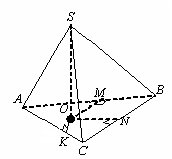Нехай у піраміді SABC: тоді за теоремою про три перпендикуляри тобто і , отже точка О – центр кола, вписаного в трикутник ABC, i OK = ON=OM, а також

SK = SN = SM.

Рис. 13

=

Отже,

Задача №2

Висота правильної чотирикутної зрізаної піраміди дорівнює 7 см. Сторони основ дорівнюють 10 см і 2 см. Знайдіть бічне ребро піраміди.

Розв’язання

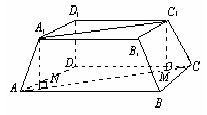Опустимо із точки С₁ перпендикуляр на основу. Це і буде висота зрізаної піраміди С₁М. Аналогічно А₁N – також висота зрізаної піраміди.

Таким чином, А₁N = C₁M ( за побудовою).

AA₁N = CC₁M ( за катетом і гіпотенузою),

отже, АN = CM.

Рис. 14

Бічне ребро АА₁ можна визначити за теоремою Піфагора із AA₁N.

, де А₁N = 7см (за умовою). Необхідно знайти AN.

Оскільки AN = CM (як доведено вище), можна записати:

2AN = AC - A₁C₁ , де AC і A₁C₁ – діагоналі основ.

АС = АВ = 10 (см); А₁С₁ = А₁В₁ = 2 (см).

Отже, (см). Тоді бічне ребро дорівнюватиме: (см). АА₁ = 9 см.

Відповідь. 9 см.

ЗАДАЧІ

1. Скільки граней, ребер має п-кутна піраміда?

2. Чи можуть бічні ребра піраміди бути рівними, якщо в її основі лежить:

1. прямокутник;

2. ромб (відмінний від квадрата);

3. правильний шестикутник;

4. трапеція?

3. Чи можуть бічні грані піраміди бути однаково нахилені до основи піраміди, якщо в основі піраміди лежить:

1. прямокутник (відмінний від квадрата);

2. ромб;

3. трапеція?

4. Скільки бічних граней, перпендикулярних до площини основи, може мати піраміда?

5. Кожне ребро тетраедра дорівнює а. Знайдіть площу його поверхні.

6. У чотирикутній піраміді кожне ребро дорівнює а. Знайдіть площу її поверхні.

7. Студент міркує: „Трикутна піраміда називається тетраедром. Отже, правильна трикутна піраміда – це правильний тетраедр”. Чи правий він? Чи кожна правильна піраміда є правильним тетраедром?

8. Знайдіть площу поверхні тетраедра, вершини якого – точки О(0;0;0;), А(2;0;0), В(0;2;0), С(0;0;2).

9. Бічне ребро правильної чотирикутної піраміди дорівнює b і нахилене до площини основи під кутом α. Знайдіть:

1. висоту піраміди;

2. радіус кола, описаного навколо основи;

3. діагональ основи;

4. площу діагонального перерізу;

5. сторону основи.

10. Апофема правильної трикутної піраміди дорівнює m і нахилена до площини основи під кутом α. Знайдіть:

1. висоту піраміди;

2. радіус кола, вписаного в основу;

3. радіус кола, описаного навколо основи;

4. сторону основи;

5. площу основи;

6. площу бічної грані.

11. Основа піраміди – рівнобедрений трикутник, основа якого дорівнює 12 см, а бічна сторона 10 см. Бічні грані утворюють з основою рівні двогранні кути, які містять по 45⁰. Знайдіть висоту піраміди.

12. Основа піраміди – прямокутний трикутник з катетами 6 см і 8 см. Усі двогранні кути при основі піраміди дорівнюють 60⁰. Знайдіть висоту піраміди.

13. Основа піраміди – прямокутник із сторонами 6 см і 8 см. Кожне бічне ребро піраміди дорівнює 13 см. Обчисліть висоту піраміди.

14. Основа піраміди – паралелограм, сторони якого 3 см і 7 см, а одна з діагоналей 6 см, висота піраміди проходить через точку перетину діагоналей і дорівнює 4 см. Знайдіть бічне ребро піраміди.

15. За даною стороною основи а і висотою b знайдіть апофему правильної піраміди: а) трикутної; б) чотирикутної; в) шестикутної.

16. Основа піраміди - рівнобедрений трикутник із сторонами 40 см, 25 см і 25см. Її висота проходить через вершину кута, протилежного стороні 40 см, і дорівнює 8 см. Знайдіть бічну поверхню піраміди.

17. Основа піраміди – квадрат, її висота проходить через одну з вершин основи. Знайдіть бічну поверхню піраміди, якщо сторона основи дорівнює 20 дм, а висота 21 дм.

18. Висота правильної чотирикутної піраміди дорівнює 7 см, а сторона основи 8 см. Знайдіть бічне ребро.

19. У правильній чотирикутній піраміді бічна поверхня дорівнює 14,76 м², а повна поверхня 18 м². Знайдіть сторону основи і висоту піраміди.

20. У чотирикутній зрізаній піраміді сторони однієї основи дорівнюють 6 см, 7 см, 8 см і 9 см, а менша сторона другої основи дорівнює 5 см. Знайдіть решту сторін цієї основи.

21. Висота піраміди дорівнює 16 м. Площа основи дорівнює 512 м². На якій відстані від основи знаходиться переріз, паралельний їй, якщо площа перерізу 50 м²?

22. Сторони основ правильної зрізаної трикутної піраміди 4 дм і 1 дм. Бічне ребро 2 дм. Знайдіть висоту піраміди.

23. У правильній чотирикутній зрізаній піраміді висота дорівнює 2 см, а сторони основи 3 см і 5 см. Знайдіть діагональ цієї піраміди.

24. Висота правильної чотирикутної зрізаної піраміди дорівнює 4 см. Сторони основ дорівнюють 2 см і 8 см. Знайдіть площі діагональних перерізів.

25. У правильній чотирикутній зрізаній піраміді сторони основ 8 м і 2 м. Висота дорівнює 4 м. Знайдіть повну поверхню.

26. Скільки кілограмів покрівельного заліза завтовшки 1 мм потрібно на покриття даху, який має форму правильної чотирикутної піраміди із стороною 4,2 м при довжині схилу 6,5 м ? На шви та обрізки добавляєть-ся 10 %. Розміри листа заліза 1400×700 мм. Визначити кількість листів, витрачених на покриття даху.