Контрольні запитання

1. Дайте означення прямого кругового конуса ( вершина, твірна, основа, висота, вісь, осьовий переріз конуса).

2. Що є осьовим перерізом прямого кругового конуса?

3. Що таке зрізаний конус?

4. Чому дорівнює об’єм конуса?

5. Виведіть формулу для об’єму конуса.

6. Запишіть формулу для знаходження об’єму зрізаного конуса.

Тема: Обчислення об’єму кулі

Мета заняття: формування вмінь знаходити об’єм кулі

ОБ’ЄМ КУЛІ	ОБ’ЄМ ЧАСТИН КУЛІ
	СЕГМЕНТ	СЕКТОР
, де R -- радіус кулі ( див. рис.18, ст.29)	де R – радіус кулі, Н – висота сегмента (див.рис.19, ст.29)	, де R – радіус кулі, Н – висота відповідного кульового сегмента (див.рис.20, ст.29)

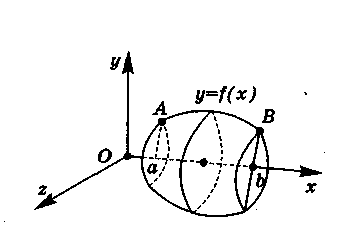
ЗАГАЛЬНА ФОРМУЛА ДЛЯ ОБ’ЄМІВ ТІЛ ОБЕРТАННЯ

О Рис. 31 б’єм тіла обертання, утвореного в результаті обертання кривої , дорівнює:

Р ОЗГЛЯНЕМО ПРИКЛАД

Задача

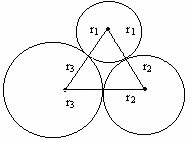
Відстань між центрами трьох куль, які попарно зовнішньо дотикаються, дорівнюють 6 см, 8 см і 10 см. Знайдіть об’єми цих куль.

Розв’язання

Нехай – радіуси шуканих куль, тоді: Додавши ці рівності, одержимо:

Рис.32

Отже, Шукані об’єми V₁, V₂, V₃ цих куль: (см³).

Відповідь.

ЗАДАЧІ

1. Чи поділяє діаметральний переріз кулю на два рівновеликі тіла?

2. Чи можна з двох металевих куль з радіусами 1см відлити кулю з радіусом 2см?

3. Радіус кулі дорівнює 9 см. Знайдіть об’єм кулі.

4. Знайдіть об’єм кулі, діаметр якої дорівнює 12 см.

5. Знайдіть радіус кулі, об’єм якої дорівнює 36 π дм³.

6. Радіуси трьох куль дорівнюють 3 см, 4 см і 5 см. Знайдіть радіус кулі, об’єм якої дорівнює сумі об’ємів даних куль.

7. Відношення об’ємів двох куль дорівнює 8. У скільки разів радіус однієї кулі більший за радіус другої кулі?

8. Зовнішній діаметр порожнистої кулі 18 см. Товщина стінок 3 см. Знайдіть об’єм матеріалу, з якого виготовлено кулю.

9. Ребро куба дорівнює а. Знайдіть об’єм вписаної кулі.

10. Ребро куба дорівнює а. Знайдіть об’єм описаної кулі.

11. З циліндра, осьовий переріз якого – квадрат із стороною 10 см, коваль викував кулю. Знайдіть радіус цієї кулі.

12. Пересипаючи пісок з порожнистої півкулі радіуса R у конус, радіус і висота якого дорівнюють R, студент дійшов висновку, що об’єм півкулі у два рази більший від об’єму конуса. Чи відповідає результат цього експерименту теорії?

13. Чавунна куля регулятора має масу 10 кг. Знайдіть діаметр кулі (густина чавуну 7,2 г/см³).

14. Маємо шматок свинцю масою 1 кг. Скільки кульок діаметром 1 см можна відлити із цього шматка? (Густина свинцю 11,4 г/см³).

15. Котел, що має форму півкулі, вміщує 28,6 л води. Визначити діаметр котла.

16. З куба виготовили найбільшу кулю. Скільки процентів матеріалу сточено? (Ця задача має застосування на підшипниковому заводі).