Контрольні запитання

1. Що таке прямий круговий циліндр (твірна, основи, бічна поверхня, радіус, вісь, осьовий переріз циліндра)?

2. Які властивості мають основи циліндра?

3. Які властивості мають твірні циліндра?

4. Яку властивість має вісь циліндра щодо його основ і твірних?

5. Чому дорівнює об’єм циліндра?

6. Виведіть формулу для об’єму циліндра.

Тема: Обчислення об’єму конуса

М ета заняття: формування вмінь знаходити об’єм конуса та зрізаного конуса.

ОБ’ЄМ КОНУСА	ОБ’ЄМ ЗРІЗАНОГО КОНУСА
де S0 – площа основи, Н – висота конуса. R – радіус основи (див. рис.16, ст.24)	де R – радіус більшої основи, r – радіус меншої основи, h – висота зрізаного конуса (див. рис.17, ст.24)

Р ОЗГЛЯНЕМО ПРИКЛАДИ

Задача №1

Твірна конуса l нахилена, до площини основи під кутом 30^о. Знайдіть висоту.

Р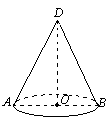 озв’язання

Із прямокутного знайдемо висоту DO, :

Відповідь.

Рис.29

Задача №2

Соснова колода довжиною 15,5 м має діаметри кінців 4 2см і 25 см. Яку помилку ( в процентах) допускають, обчислюючи об’єм колоди, при множенні довжини на площу поперечного перерізу по середині колоди?

Р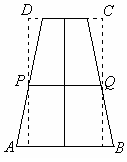 озв’язання

Колода має форму зрізаного конуса. Візьмемо осьовий переріз, це буде рівнобічна трапеція ABCD з основами, що дорівнюють діаметрам колоди, і висотою, яка дорівнює висоті колоди.

Д

Рис. 30

іаметр поперечного перерізу колоди в її середині дорівнює PQ – середній лінії трапеції. Об’єм зрізаного конуса:

Об’єм циліндра діаметром PQ і висотою Н дорівнює: (м).

(м³). Знайдемо помилку:

Помилка приблизно дорівнює 2%.

Відповідь. 2%.

ЗАДАЧІ

1. Чи правильно, що об’єм прямого кругового конуса збільшиться вдвічі, якщо збільшити вдвічі радіус його основи?

2. Чи є рівними між собою об’єми конусів, утворених обертанням прямокутного трикутника навколо нерівних катетів?

3. Чи правильно, що всі конуси, які мають спільну основу, а їхні вершини розміщені в площині, паралельній основі, рівновеликі між собою?

4. Знайдіть об’єм конуса, радіус якого дорівнює 6 см, а висота 8 см.

5. Висота конуса дорівнює 6 см, твірна – 10 см. Знайдіть об’єм конуса.

6. Осьовий переріз конуса – прямокутний трикутник із гіпотенузою 12 см. Знайдіть об’єм конуса.

7. Осьовий переріз конуса – прямокутний трикутник із катетами 6 см. Знайдіть об’єм конуса.

8. Осьовим перерізом конуса є рівнобедрений прямокутний трикутник, площа якого 9 м². Знайдіть об’єм конуса.

9. Довжина твірної конуса дорівнює l, а довжина кола основи С. Знайдіть об’єм конуса.

10. Купа щебеню має конічну форму, радіус основи якої 2 м, а твірна 3,5 м. Знайдіть об’єм купи щебеню.

11. Стіжок сіна має форму циліндра з конічним верхом. Радіус його основи 2,5 м, висота 4 м, причому циліндрична частина стіжка має висота 2,2 м. Густина сіна 0,03 г/см³. Визначте масу стіжка сіна.

12. Рідина, налита в конічну посудину висотою 0,18м і діаметром основи 0,24м, переливається в циліндричну посудину, діаметр основи якої 0,1 м. Як високо знаходитиметься рівень рідини в посудині?

13. Рівносторонній трикутник обертається навколо своєї сторони а. Знайдіть об’єм утвореного тіла обертання.

14. Прямокутний трикутник з катетами a i b обертається навколо гіпотенузи . Знайдіть об’єм утвореного тіла.

15. Чи правильно, що переріз конуса, який паралельний площині основи конуса і поділяє навпіл твірну, відтинає від нього конус з об’ємом вчетверо меншим за об’єм даного конуса?

16. Радіуси основ зрізаного конуса R і r, твірна нахилена до площини основи під кутом 45^о. Знайдіть об’єм.

17. Знайдіть об’єм зрізаного конуса, радіуси основ якого дорівнюють 1 см і 9 см, а висота – 6 см.

18. Радіуси основ зрізаного конуса дорівнюють 3 см і 6 см, а твірна – 5 см. Знайдіть об’єм зрізаного конуса.

19. Об’єм зрізаного конуса дорівнює 584π см³, а радіус основ – 10 см і 7 см. Знайдіть висоту конуса.

20. Об’єм зрізаного конуса дорівнює 248π см³, його висота 8 см, радіус однієї основи – 4 см. Знайдіть радіус другої основи зрізаного конуса.

21. Рівнобічна трапеція з основами см і см і кутом 60^о обертається навколо своєї осі симетрії. Знайдіть об’єм тіла обертання.

22. Висота зрізаного конуса дорівнює 3 см. Радіус однієї основи вдвічі більший радіуса другої основи, а твірна нахилена до площини основи під кутом 45^о. Знайдіть об’єм зрізаного конуса.

23. Із жерсті вирізали сектор радіусом 50 см і центрувальним кутом 216^о і загорнули в конус. Знайти об’єм конуса.