2.3. Численное значение производной. Геометрическое и механическое истолкование производной.

1. Численное значение производной.

Производная от функции у = f (x) представляет собою, как мы видели, также функцию от х. При решении многих задач бывает необходимо получить численное значение производной в данной точке, т. е. при данном значении аргумента. Обычно отыскание численного значения производной не вызывает никаких затруднений: для решения этой задачи достаточно в общее выражение производной подставить соответствующее значение аргумента. Встречаются, однако, исключительные случаи, когда для нахождения значения производной в данной точке приходится обращаться к определению производной как предела отношения приращений (см. раздел I); в этих случаях техника дифференцирования не может быть использована.

Ниже приводится несколько примеров на определении численного значения производной как в простейших, так и в более трудных случаях.

Примеры решения задач.

25. Найти f^/ (1), если f (x) = x³ – 5x² + 8x + 2.

Находим производную от заданной функции: f^/ (x)= 3x² – 10x + 8. Далее подставляем в выражение для производной вместо х единицу: f^/ (1) = 3·1 – 10·1 + 8 =1.

26. Найти f^/ (0), если

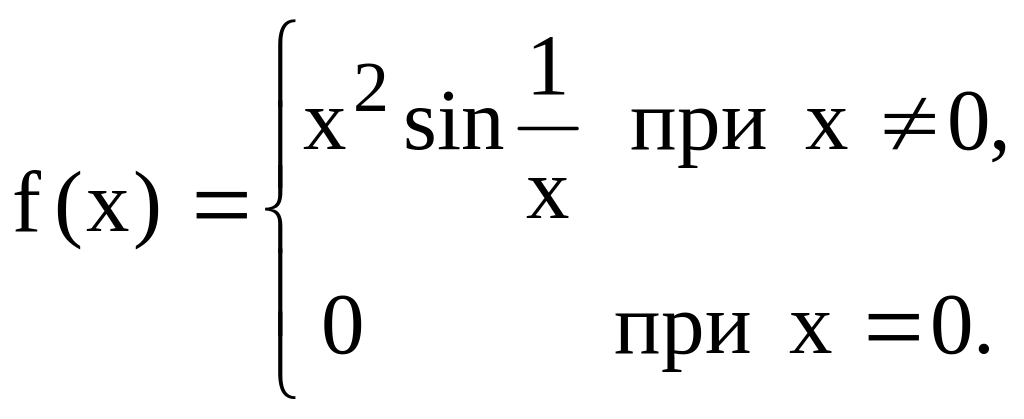
Выражение , а также производная от этого выражения не имеют смысла при х = 0. Вычисляем f^/ (0) непосредственно, пользуясь определением производной. В соответствии с этим определением

где h – приращение аргумента.

При х = 0 имеем: .

В данном случае

Таким образом,

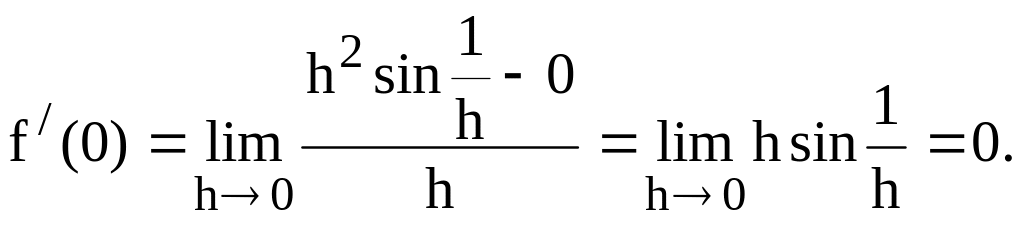
2. Геометрический смысл производной.

Пусть у = f(x) – уравнение некоторой кривой, а М (х₁; у₁) – точка, лежащая на этой кривой, так что у₁ = f (x₁).

З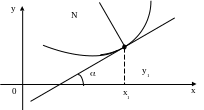 начение производной от функции f (x) при х = х₁ равно угловому коэффициенту касательной к данной кривой, проходящей через точку М (х₁; у₁). Иначе говоря, f^/ (x₁) = tg , где  – угол между касательной к данной кривой, проведенной через точку М, и положительным направлением оси абсцисс.

У

М (х₁; у₁)

равнение касательной к данной кривой у = f (x), проходящей через точку М (х₁; у₁) кривой, имеет вид:

у – у₁ = f^/ (x₁) (x – x₁). (1)

Нормалью MN к кривой в данной ее точке М (х₁; у₁) называется перпендикуляр к касательной, проведенный через точку касания. Уравнение нормали MN записывается так:

у – у₁ = (x – x₁). (2)

Указание на геометрический смысл производной позволяет легко решать некоторые задачи аналитической геометрии.

Примеры решения задач.

27. Найти уравнение касательной и нормали к кривой у = х³ + 2х в точке М (1; 3).

Для определения углового коэффициента касательной находим производную от заданной функции: у^/ = 3х² + 2. Значение производной в точке М (1; 3) и дает искомый угловой коэффициент к = 3·1 + 2 = 5. Таким образом, уравнение касательной:

у – 3 = 5 (х – 1), или 5х – у – 2 = 0,

а уравнение нормали у – 3 = - 1/5 (х – 1), или х + 5у – 16 = 0.

28. Определить, под каким углом парабола у = х² – х пересекает ось абсцисс.

Находим абсциссы точек пересечения кривой у = х² – х и оси Ох, уравнение которой у = 0. Решая совместно оба уравнения, получаем х² – х = 0, откуда заключаем, что абсциссы искомых точек х = 0 и х = 1.

Под углом кривой с осью Ох понимается угол, который касательная к этой кривой в соответствующей точек образует с сою абсцисс. Для решения поставленной задачи следует найти угловые коэффициенты касательных к параболе в точках с абсциссами х = 0 и х = 1.

Производная от функции у = х² – х будет у^/ = 2х – 1. обозначая через ₁ и ₂ углы, образованные с осью абсцисс касательными к параболе, проведенными соответственно через точки (0; 0) и (1; 0), имеем:

tg α₁ = 2·0 – 1 = – 1 и tg α₂ = 2·1 – 1 = 1, так что α₁ = 135⁰ и α₂ = 45⁰.