2.4. Определенный интеграл.

Определение: Фигура, ограниченная кривой , отрезком оси , прямыми и называется криволинейной трапецией.

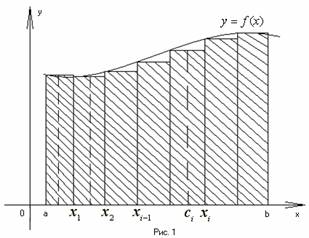
Для вычисления площади этой криволинейной трапеции разобьем отрезок произвольным образом на частей и обозначим точки деления , причем , а .

Восстановим из этих точек перпендикуляры до пересечения с кривой, получим значения функции в этих точках: . В результате этого площадь криволинейной трапеции окажется разбитой на сумму площадей элементарных криволинейных трапеций. В отрезках , , , , , возьмем совершенно произвольно точки и восстановим перпендикуляры из этих точек до пересечения с кривой . Получим значения .

Далее построим ступенчатую фигуру, состоящую из прямоугольников, имеющих своими основаниями отрезки , а высотами . Эта фигура ограниченна ломаной линией. Площадь этой ступенчатой фигуры можно считать приближенным значением площади заданной криволинейной трапеции, причем тем более точной, чем больше и чем меньше длины отрезков .

Площадь равна сумме площадей прямоугольников, построенных на отрезках:

(1)

Если теперь в (1) неограниченно увеличить число так чтобы длина наибольшего из отрезков стремилась к нулю, т. е. , то площадь криволинейной трапеции будет равна пределу суммы (1).

(2)

Сумма (1) называется интегральной суммой.

Определение: Если существует конечный предел интегральной суммы при условии, что , то этот предел называют определенным интегралом от функции на и обозначают .Т. об. По определению

Числа и называются нижним и верхним пределами интегрирования соответственно. Определенный интеграл выражает число.

Свойства определенного интеграла.

1. 3.

2. 4.

Теорема: Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования.

(3)

Формула (3) называется формулой Ньютона – Лейбница и дает практически удобный метод вычисления определенного интеграла в том случае, когда известна первообразная подынтегральной функции.

Основными методами интегрирования определенного интеграла являются те же, что и для неопределенного.

2.5. Приложения определенного интеграла.

1. Вычисление площадей плоских фигур.

а) если непрерывная кривая задана уравнением , где

б) если непрерывная кривая задана уравнением , где

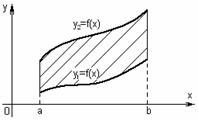
в) если площадь ограничена двумя непрерывными кривыми и , ( ), прямыми и

2. Объем тела вращения.

а) вокруг оси :

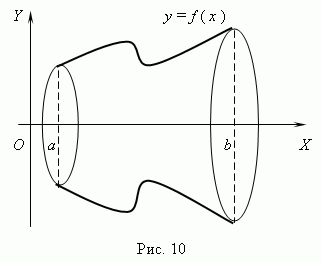
б) вокруг оси :