Введение.

Цель математической подготовки студентов-медиков–это ознакомление с основными понятиями и методами современного математического аппарата, необходимого для решения задач физического, химического, биологического и другого характера, которые будут встречаться в процессе изучения профилирующих дисциплин, а так же в дальнейшей профессиональной деятельности.

Раздел 1. Математический анализ

§1. Функция. Производная функции .

1.1. Функция, способы её задания.

Определение: Функцией называется закон или соответствие , по которому каждому значения переменной ставиться в соответствие единственное значение переменной .

Переменная при этом называется аргументом или независимой переменной, а - функцией или зависимой переменной. Относительно самих величин и говорят, что они находятся в функциональной зависимости. Эту зависимость сокращенно обозначают , где символ называется характеристикой функции.

Если каждому значению переменной соответствует одно значение , то функция называется однозначной. Если хотя бы некоторым значениям переменной соответствует несколько значений , то функция называется многозначной.

Определение: Совокупность всех значений независимой переменной , для которых функция определена, называется областью определения или областью существования функции. Обозначается: .

Определение: Областью значений функции называются все допустимые значения переменной . Обозначается: .

Обычно рассматривают 3 способа задания функций:

1) аналитический. Здесь функция выражена при помощи формулы. Например: .

2) Табличный. Здесь дается ряд числовых значений и вычисляются соответствующие значения . Например:

	0	1	-1	2	-2
	0	1	1	4	4

3) графический. Графиком функции называется множество всех точек в плоскости , координаты которых связаны данной функциональной зависимостью.

1.2. Производная. Правила дифференцирования. Производные основных элементарных функций.

Определение: Производной функции в точке называется предел приращения функции к приращению аргумента , когда , при условии что этот предел существует.

.

.

Процесс нахождения производной называется дифференцированием. Функция называется дифференцируемой, если она имеет производную.

Геометрический смысл производной.

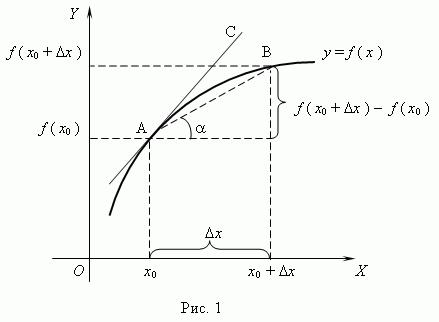
Пусть дана кривая . Возьмем на ней точку и дадим аргументу приращение . Тогда получим новый аргумент и новое значение функции , т. е. мы получили новую точку на кривой и обозначим её через . Проведем секущую и обозначим угол наклона секущей к оси через . Рассмотрим прямоугольный треугольник :

.

При точка перемещается вдоль кривой, приближаясь к точке . Секущая поворачивается вокруг точки и величина угла изменяется. При приближении секущей к касательной угол приближается к углу .

.

Итак, геометрический смысл производной: угловой коэффициент касательной к графику функции в данной точке равен значению её производной в точке касания;

уравнение касательной: .

уравнение нормали: .

физический (механический) смысл производной: мгновенная скорость материальной точки есть первая производная от пути по времени :

Правила дифференцирования.

1. ; 4. ;

2. ; 5. ;

3. ; 6. .

Производные основных элементарных функций.

1. 1.

2. 2.

3. 3.

4. 4.

5. 5.

6. 6.

7. 7.

8. 8.

9. 9.

10. 10.

11. 11.

12. 12.

13. 13.