3. Параболическая модель

Пусть эконометрическая модель специфицирована в параболической форме [ЛЕЩ, c. 58]:

Y = a₀ + a₁X + a₂X² + u,

где a₀, a₁, a₂ - параметры модели u - стохастическая составляющая (остатки), X – фактор, Y - показатель.

Оценим параметры модели методом МНК:

A = (X 'X)^-1X 'Y,

где матрица X характеризует все независимые переменные модели. Поскольку модель имеет свободный член a₀, для которого все x_i = 1, то матрицу нужно дополнить первым столбцом, в котором все члены являются единицами, X ' - транспонированная матрица к данной, а вектор Y - вектор зависимой переменной.

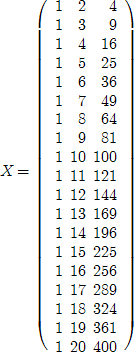
Транспонируем данную матрицу:

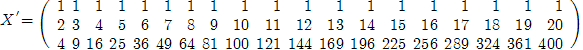
Найдем произведение транспонированной матрицы и данной:

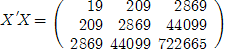
Вычислим обратную матрицу:

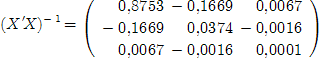
Найдем произведение транспонированной матрицы и вектора Y:

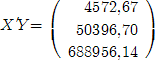
Умножив обратную матрицу на предыдущую, получим искомые коэффициенты:

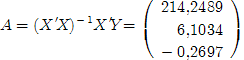
Таким образом a₀ = 214,2489, a₁ = 6,1034, a₂ = -0,2697.

Следовательно, параболическая модель имеет вид:

Y = 214,2489 + 6,1034X - 0,2697X².

Проверку правильности решения можно выполнить, использовав стандартную функцию Excel ЛИНЕЙН() [ЛАВ, c. 249]. Задав первым ее параметром значения диапазона Y, а вторым - диапазона X, получим аналогичный результат.

Выполним построение корреляционного поля с изображением на нем линии регрессии.

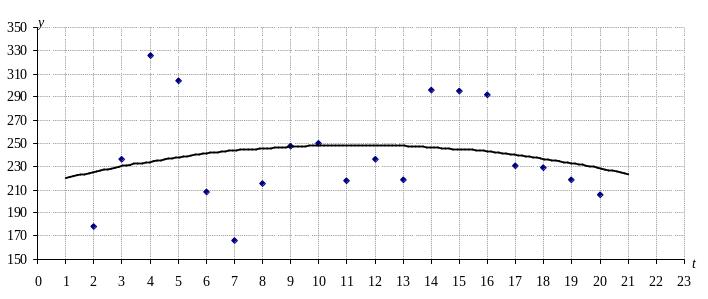
Найдем совокупный коэффициент детерминации и коэффициент множественной корреляции и охарактеризуем степень совместимого влияния факторов на показатель.

Для этого построим расчетную таблицу.

№	Y	X1	X2	(X1 - X1c)2	(X2 - X2c)2	Yp	(Y - Yc)2	(Y - Yp)2
1	178	2	4	81	21609	225,3771	3927,1331	2244,5880
2	236,67	3	9	64	20164	230,1322	15,9747	42,7433
3	326	4	16	49	18225	234,3479	7281,7478	8400,1063
4	303,67	5	25	36	15876	238,0243	3969,3979	4309,3554
5	208	6	36	25	13225	241,1614	1067,1226	1099,6785
6	166,33	7	49	16	10404	243,7591	5525,9661	5995,2732
7	215,33	8	64	9	7569	245,8176	641,9556	929,4917
8	247,67	9	81	4	4900	247,3367	49,0442	0,1111
9	250,33	10	100	1	2601	248,3164	93,3766	4,0546
10	218	11	121	0	900	248,7568	513,7857	945,9822
11	236,67	12	144	1	49	248,6579	15,9747	143,7101
12	218,33	13	169	4	324	248,0197	498,9345	881,4764
13	295,67	14	196	9	2025	246,8421	3025,3474	2384,1645
14	295,33	15	225	16	5476	245,1252	2988,0608	2520,5235
15	292,33	16	256	25	11025	242,8689	2669,0819	2446,3960
16	230,67	17	289	36	19044	240,0734	99,9369	88,4234
17	229	18	324	49	29929	236,7385	136,1152	59,8839
18	218,67	19	361	64	44100	232,8642	483,8611	201,4762
19	206	20	400	81	62001	228,4507	1201,7899	504,0322
Σ	4572,67	209,00	2869,00	570,0000	289446,0000	-	34204,6068	33201,4706

Средние значения переменных соответственно равны:

Вычислим дисперсии независимых переменных, зависимой переменной и остатков:

Коэффициент детерминации R² показывает, какая часть движения зависимой переменной описывается данным регрессионным уравнением и вычисляется по формуле [ЛЕЩ, c. 48]:

и коэффициент корреляции:

Поскольку |r| < 0,4, то между факторным и результативным признаком корреляционной связи нет.

Коэффициент детерминации равен: R² = 0,0293. А это значит, что 2,93% вариации результативного признака зависит от вариации уровня факторных признаков, а 97,07% приходится на другие факторы.

Найдем среднюю ошибку аппроксимации как среднюю арифметическую простую по формуле [ЕЛИ, с. 87]:

Получим:

Поскольку δ > 7%, то делаем вывод о плохом подборе модели для исходных данных.

Проверим адекватность модели по критерию Фишера или F-критерию, который вычисляется по формуле [ЛЕЩ, c. 53]:

Поскольку F(0,05; 2; 16) = 3,6337 и |F*| > F_таб, то делаем вывод о неадекватности эконометрической модели.

Методом математической экстраполяции составим прогноз показателя на следующие 4 недели.

Y(22) = 214,2489 + 6,1034 ∙ 22 - 0,2697 ∙ 22² = 217,9889,

Y(23) = 214,2489 + 6,1034 ∙ 23 - 0,2697 ∙ 23² = 211,9558,

Y(24) = 214,2489 + 6,1034 ∙ 24 - 0,2697 ∙ 24² = 205,3833,

Y(25) = 214,2489 + 6,1034 ∙ 25 - 0,2697 ∙ 25² = 198,2714.

Таким образом, делаем вывод о несостоятельности исходных данних для построения адекватной модели. Об этом свидетельствует непредсказуемость объемов продаж рекламного времени.

Для возможности повышения прибыльности этого вида деятельности нужно кардинально менять подход в работе персонала, вид рекламируемых продуктов и качество их подачи.

Нужно делать ставку на долгосрочные контракты с новыми заказчиками рекламы и находить компромисс с прежними клиентами. Для этого нужно усовершенствовать тарифные планы рекламных пакетов.