Задача 1.

В табл. 1 приведены данные о личных потребительских расходах и располагаемом личном доходе населения США (млрд. дол., в ценах 1972 г.) за период с 1959 г. по 1983 г.

а) Постройте уравнение для функции спроса (Y) на данный товар или вид услуг в зависимости от располагаемого личного дохода (X). Постройте таблицу дисперсионного анализа. Вычислите коэффициент детерминации R².

Проверьте регрессию на значимость с помощью F-теста (α = 0,05 - критерий значимости). Вычислите 95% доверительные интервалы для истинных значений коэффициентов в этом уравнении. Изобразите диаграмму рассеяния и прямую регрессии.

б) Постройте линейный временной тренд для функции спроса.

в) Рассмотрите функцию спроса (Y) как функцию двух переменных: располагаемого дохода (X) и реальной цены на товар или вид услуг (P). (Реальная цена вычисляется по формуле P = (Z / L) ∙ 100%). (Z, L см. табл. 1).

Постройте уравнение множественной регрессии Y на X и P. С помощью МНК оцените коэффициенты в этом уравнении (замените Y, X и P на их логарифмы).

Дайте экономическую интерпретацию коэффициентов в уравнении. Вычислите коэффициенты эластичности функции спроса. Интерпретируйте эти коэффициенты.

Таблица 1

Исходные данные о личных потребительских расходах и располагаемом личном доходе

Год	Личный располагаемый доход, млрд. $	Текущие расходы на бензин	Дефляторы цен для личных потребительских расходов	Цены
T	X	Y	Z	L
1959	440,4	13,7	82,2	70,6
1960	452,0	14,2	84,5	71,9
1961	461,4	14,3	83,9	72,6
1962	482,0	14,9	84,5	73,7
1963	500,5	15,3	84,5	74,8
1964	528,0	16,0	84,4	75,9
1965	557,5	16,8	87,5	77,2
1966	646,8	17,8	89,5	79,4
1967	673,5	18,4	92,4	81,4
1968	701,3	19,9	93,8	84,6
1969	722,5	21,4	97,0	88,4
1970	751,6	22,9	97,9	92,5
1971	779,2	24,2	98,7	96,3
1972	810,3	25,4	109,0	100,0
1973	865,3	26,2	109,4	105,7
1974	858,4	24,8	147,7	116,3
1975	875,8	25,6	157,7	125,2
1976	906,8	26,8	164,3	131,7
1977	942,9	27,7	173,7	139,3
1978	988,8	28,3	181,3	149,1
1979	1015,5	27,4	243,2	162,5
1980	1021,6	25,1	337,9	179,0
1981	1049,3	25,1	376,4	194,3
1982	1058,3	25,3	356,6	206,0
1983	1095,4	26,1	344,9	213,6

Решение

а) Постройте уравнение для функции спроса (Y) на данный товар или вид услуг в зависимости от располагаемого личного дохода (X). Постройте таблицу дисперсионного анализа. Вычислите коэффициент детерминации R².

Проверьте регрессию на значимость с помощью F-теста (α = 0,05 - критерий значимости). Вычислите 95% доверительные интервалы для истинных значений коэффициентов в этом уравнении. Изобразите диаграмму рассеяния и прямую регрессии.

Идентифицируем переменные: x - независимая переменная (фактор) y - зависимая переменная (показатель).

Пусть эконометрическая модель специфицирована в линейной форме:

y = ax + b + u

где a, b - параметры модели u - стохастическая составляющая (остатки).

Используем метод наименьших квадратов [ЛЕЩ, с.29]. Запишем систему нормальных уравнений, используя в качестве неизвестной переменной - переменную x:

где n - количество наблюдений.

Построим вспомогательную таблицу 1.

Табл. 1.

№	x	y	x2	xy
1	440,4	13,7	193952,16	6033,48
2	452,0	14,2	204304,00	6418,40
3	461,4	14,3	212889,96	6598,02
4	482,0	14,9	232324,00	7181,80
5	500,5	15,3	250500,25	7657,65
6	528,0	16,0	278784,00	8448,00
7	557,5	16,8	310806,25	9366,00
8	646,8	17,8	418350,24	11513,04
9	673,5	18,4	453602,25	12392,40
10	701,3	19,9	491821,69	13955,87
11	722,5	21,4	522006,25	15461,50
12	751,6	22,9	564902,56	17211,64
13	779,2	24,2	607152,64	18856,64
14	810,3	25,4	656586,09	20581,62
15	865,3	26,2	748744,09	22670,86
16	858,4	24,8	736850,56	21288,32
17	875,8	25,6	767025,64	22420,48
18	906,8	26,8	822286,24	24302,24
19	942,9	27,7	889060,41	26118,33
20	988,8	28,3	977725,44	27983,04
21	1015,5	27,4	1031240,25	27824,70
22	1021,6	25,1	1043666,56	25642,16
23	1049,3	25,1	1101030,49	26337,43
24	1058,3	25,3	1119998,89	26774,99
25	1095,4	26,1	1199901,16	28589,94
Σ	19185,1	543,6	15835512,07	441628,55

Получим систему уравнений:

Решение системы найдем по формулам Крамера [ГЕТ, с.30]:

где Δ - главный определитель системы.

Следовательно, уравнение линейной модели имеет вид:

y = 4,8705 + 0,0220x.

Это значит, что при увеличении или уменьшении значения фактора на 1 у.е. показатель увеличивается или уменьшается на 0,022 у.е., то есть между эконометрическими параметрами существует прямая пропорциональная или положительная зависимость.

Свободный член регрессии b = 4,8705 указывает значение показателя при нулевом значении фактора. Он имеет лишь расчетное значение, поскольку такой случай невозможен в реальной экономической ситуации.

Для проведения исследования модели построим вспомогательную таблицу 2.

Табл. 2.

№	x	y	yx					u2 = (y - yx)2
1	440,4	13,7	14,5539	64,7059	106931,6160	2630,4202	51,6973	0,7292
2	452,0	14,2	14,8090	56,9119	99479,6832	2379,4078	48,0945	0,3709
3	461,4	14,3	15,0157	55,4131	93638,4480	2277,8938	45,2705	0,5122
4	482,0	14,9	15,4686	46,8403	81455,4432	1953,3050	39,3805	0,3233
5	500,5	15,3	15,8754	41,5251	71237,7452	1719,9294	34,4407	0,3311
6	528,0	16,0	16,4800	32,9935	57314,2752	1375,1366	27,7092	0,2304
7	557,5	16,8	17,1287	24,4431	44059,6892	1037,7654	21,3011	0,1080
8	646,8	17,8	19,0922	15,5551	14545,3248	475,6622	7,0321	1,6698
9	673,5	18,4	19,6793	11,1823	8817,9612	314,0150	4,2631	1,6365
10	701,3	19,9	20,2905	3,4003	4369,7388	121,8958	2,1126	0,1525
11	722,5	21,4	20,7567	0,1183	2016,3692	15,4470	0,9748	0,4139
12	751,6	22,9	21,3965	1,3363	249,7664	-18,2694	0,1208	2,2605
13	779,2	24,2	22,0034	6,0319	139,1456	28,9710	0,0673	4,8252
14	810,3	25,4	22,6872	13,3663	1840,0668	156,8278	0,8896	7,3594
15	865,3	26,2	23,8965	19,8559	9583,6268	436,2246	4,6333	5,3061
16	858,4	24,8	23,7448	9,3391	8280,2720	278,0838	4,0032	1,1135
17	875,8	25,6	24,1274	14,8687	11749,6928	417,9750	5,6805	2,1686
18	906,8	26,8	24,8090	25,5631	19431,2448	704,7862	9,3942	3,9641
19	942,9	27,7	25,6028	35,4739	30798,8460	1045,2542	14,8900	4,3984
20	988,8	28,3	26,6120	42,9811	49016,1888	1451,4722	23,6974	2,8493
21	1015,5	27,4	27,1991	31,9903	61551,6252	1403,2310	29,7578	0,0404
22	1021,6	25,1	27,3332	11,2627	64615,6064	853,0818	31,2391	4,9872
23	1049,3	25,1	27,9423	11,2627	79465,3548	946,0430	38,4184	8,0784
24	1058,3	25,3	28,1401	12,6451	84620,4828	1034,4262	40,9107	8,0664
25	1095,4	26,1	28,9559	18,9747	107581,3760	1428,7506	52,0114	8,1561
Σ	19185,1	543,6	-	608,0416	1112789,5896	24467,7356	537,9904	70,0512
Σ/n	767,404	21,744	-	24,3217	44511,5836	978,7094	21,5196	2,8020

Оценим параметры модели альтернативным способом:

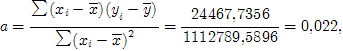
Линейное уравнение регрессии аналогично: y_x = 0,022x + 4,8705.

Вычислим для зависимой переменной y общую дисперсию, дисперсию, что объясняет регрессию, дисперсию ошибок [ЛУК, с. 56]:

Суммы квадратов связанные с определенным источником вариации, а также со степенями свободы и средними квадратами. Сведем их всех в таблице, которая называется базовой таблицей дисперсионного анализа - ANOVA-таблицей [ЛУК, с. 61].

Построим ANOVA-таблицу о зависимости между показателем и фактором:

Источник вариации	Количество степеней свободы	Сумма квадратов	Средние квадраты
Предопределено регрессией (модель)	1
Необъяснимо с помощью регрессии (ошибки)	n - 2 = 23
Общее	n - 1 = 24		-

Определим коэффициенты детерминации R² и корреляции r [ЛУК, c. 57]:

Этот результат значит, что 88,48% вариации результативного признака зависит от вариации уровня факторного признака, а 11,52% приходится на другие факторы.

Поскольку 0,7 < r < 1, то между факторным и результативным признаком корреляционная связь сильная.

Проверим адекватность модели по критерию Фишера или F-критерию, который вычисляется по формуле:

Поскольку табличное значение F_{(0,05; 1; 23)} = 4,28 и |F| > F_таб, то делаем вывод об адекватности эконометрической модели.

Оценим статистическую значимость параметров регрессии.

Табличное значение t-критерия Стьюдента при заданном уровне значимости 0,95 и n - 2 = 23 степенях свободы равно 2,07.

Найдем матрицу погрешностей C^-1, обратную к матрице системы уравнений:

Δ = |C| = 27819739,74,

Определим стандартные погрешности оценок параметров модели, учитывая дисперсию остатков:

где

Рассчитаем t-критерий Стьюдента для каждого из коэффициентов

Поскольку t_m = 2,07 и это значение больше t-критериев для каждого из коэффициентов, то делаем вывод об их статистической значимости.

Определим интервалы доверия для параметров регрессии [ЕЛИ, с. 57].

Для расчета доверительного интервала определяем предельную погрешность для каждого коэффициента:

Δ_a = t_таб.m_a = 2,0690 · 0,0017 = 0,0034,

Δ_b = t_таб.m_b = 2,0690 · 1,3167 = 2,7242,

Следовательно, экстремальные значения для каждого коэффициента следующие:

min a = a - Δ_a = 0,0220 - 0,0034 = 0,0186, max a = a + Δ_a = 0,0220 + 0,0034 = 0,0254, min b = b - Δ_b = 4,8705 - 2,7242 = 2,1463, max b = b + Δ_b = 4,8705 + 2,7242 = 7,5947.

Таким образом, доверительные интервалы для коэффициентов регрессии следующие:

a  (0,0186; 0,0254),

b  (2,1463; 7,5947).  

Изобразим диаграмму рассеяния и прямую регрессии.

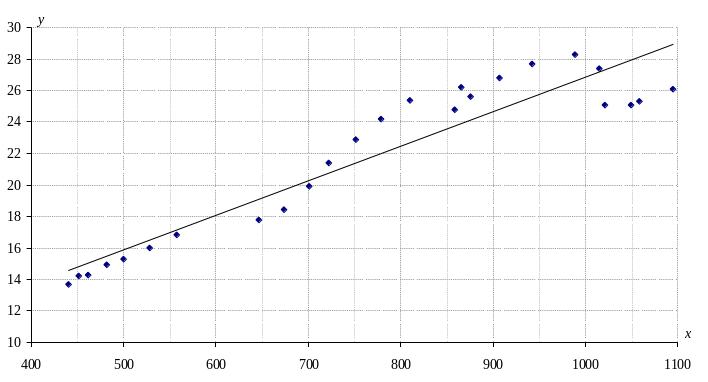
б) Постройте линейный временной тренд для функции спроса.

Идентифицируем переменные: t - независимая временная переменная (фактор), y - зависимая переменная (показатель). Пусть модель специфицирована в линейной форме:

y = at + b + u,

где a, b - параметры модели, u - стохастическая составляющая (остатки).

Используем метод наименьших квадратов [ЛЕЩ, с.29]. Запишем систему нормальных уравнений, используя в качестве неизвестную переменную - переменную t:

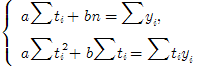
Расчет параметров значительно упрощается, если за начало счета времени (t = 0) принять центральный интервал (момент).

При нечетном числе уровней (например, 25), значения t = 0 – условного обозначения времени будет отвечать среднему 1971 году:

t	-12	-11	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0
Y	13,7	14,2	14,3	14,9	15,3	16	16,8	17,8	18,4	19,9	21,4	22,9	24,2
t	1	2	3	4	5	6	7	8	9	10	11	12
Y	25,4	26,2	24,8	25,6	26,8	27,7	28,3	27,4	25,1	25,1	25,3	26,1

Поскольку Σt = 0, поэтому система нормальных уравнений принимает вид:

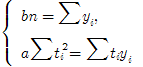
Построим вспомогательную таблицу:

№	t	y	t2	ty
1	-12	13,7	144	-164,4
2	-11	14,2	121	-156,2
3	-10	14,3	100	-143,0
4	-9	14,9	81	-134,1
5	-8	15,3	64	-122,4
6	-7	16,0	49	-112,0
7	-6	16,8	36	-100,8
8	-5	17,8	25	-89,0
9	-4	18,4	16	-73,6
10	-3	19,9	9	-59,7
11	-2	21,4	4	-42,8
12	-1	22,9	1	-22,9
13	0	24,2	0	0,0
14	1	25,4	1	25,4
15	2	26,2	4	52,4
16	3	24,8	9	74,4
17	4	25,6	16	102,4
18	5	26,8	25	134,0
19	6	27,7	36	166,2
20	7	28,3	49	198,1
21	8	27,4	64	219,2
22	9	25,1	81	225,9
23	10	25,1	100	251,0
24	11	25,3	121	278,3
25	12	26,1	144	313,2
Σ	-	543,6	1300	819,6

Получим систему уравнений:

Находим решение:

a = 819,6 / 1300 = 0,6305,

b = 543,6 / 25 = 21,744.

Следовательно, уравнение линейного тренда имеет вид:

y = 21,7440 + 0,6305t.

Это значит, что при увеличении или уменьшении значения временного фактора на 1 ед., показатель увеличивается или уменьшается на 0,6305 у.е., то есть между параметрами существует прямая пропорциональная или положительная зависимость.

Свободный член регрессии b = 21,744 указывает значение показателя при нулевом значении условного времени.

в) Рассмотрите функцию спроса (Y) как функцию двух переменных: располагаемого дохода (X) и реальной цены на товар или вид услуг (P). (Реальная цена вычисляется по формуле P = (Z / L) ∙ 100%). (Z, L см. табл. 1).

Постройте уравнение множественной регрессии Y на X и P. С помощью МНК оцените коэффициенты в этом уравнении (замените Y, X и P на их логарифмы).

Дайте экономическую интерпретацию коэффициентов в уравнении. Вычислите коэффициенты эластичности функции спроса. Интерпретируйте эти коэффициенты.

Искомое уравнение множественной регрессии выражается производственной функцией или функцией Кобба-Дугласа [НАК, c.140]:

Y = c X^a P^b,

где c - коэффициент, что отображает уровень технологической производительности, показатели a и b - коэффициенты элластичности объема производства Y по фактору производства, то есть по капиталу X и реальной цене P соответственно.

Для оценки параметров производственной регрессии сведем ее к линейной форме. После логарифмирования и замены величин получим приведенную линейную регрессию:

lgY = lg(c X^a P^b),

lgY = lgc + a lgX + b lgP.

Обозначим:

lgY = y, lgc = a₀, a = a₁, b = a₂, lgX = x₁, lgP = x₂,

где X - количество фактора 1, P - количество фактора 2, Y - показатель.

Получили эконометрическую модель, которая специфицирована в линейной форме:

y = a₀ + a₁x₁ + a₂x₂ + u,

где a₀, a₁, a₂ - параметры модели u - стохастическая составляющая (остатки).

Запишем исходные данные в такой форме.

№	Y	X	P
1	13,7	440,4	116,43
2	14,2	452	117,52
3	14,3	461,4	115,56
4	14,9	482	114,65
5	15,3	500,5	112,97
6	16,0	528	111,2
7	16,8	557,5	113,34
8	17,8	646,8	112,72
9	18,4	673,5	113,51
10	19,9	701,3	110,87
11	21,4	722,5	109,73
12	22,9	751,6	105,84
13	24,2	779,2	102,49
14	25,4	810,3	109
15	26,2	865,3	103,5
16	24,8	858,4	127
17	25,6	875,8	125,96
18	26,8	906,8	124,75
19	27,7	942,9	124,69
20	28,3	988,8	1215,96
21	27,4	1015,5	149,66
22	25,1	1021,6	188,77
23	25,1	1049,3	193,72
24	25,3	1058,3	173,11
25	26,1	1095,4	161,47

После логарифмирования получим исходные данные для расчетов.

№	y	x1	x2		№	y	x1	x2
1	1,1367	2,6438	2,0661		14	1,4048	2,9086	2,0374
2	1,1523	2,6551	2,0701		15	1,4183	2,9372	2,0149
3	1,1553	2,6641	2,0628		16	1,3945	2,9337	2,1038
4	1,1732	2,6830	2,0594		17	1,4082	2,9424	2,1002
5	1,1847	2,6994	2,0530		18	1,4281	2,9575	2,0960
6	1,2041	2,7226	2,0461		19	1,4425	2,9745	2,0958
7	1,2253	2,7462	2,0544		20	1,4518	2,9951	3,0849
8	1,2504	2,8108	2,0520		21	1,4378	3,0067	2,1751
9	1,2648	2,8283	2,0550		22	1,3997	3,0093	2,2759
10	1,2989	2,8459	2,0448		23	1,3997	3,0209	2,2872
11	1,3304	2,8588	2,0403		24	1,4031	3,0246	2,2383
12	1,3598	2,8760	2,0246		25	1,4166	3,0396	2,2081
13	1,3838	2,8916	2,0107

Построим модель множественной линейной регрессии.

Пусть эконометрическая модель специфицирована в линейной форме [ЛЕЩ, c. 58]:

Y = a₀ + a₁X₁ + a₂X₂ + u,

где a₀, a₁, a₂ - параметры модели u - стохастическая составляющая (остатки), X₁, X₂ - факторы Y - показатель. Оценим параметры модели методом МНК:

A = (X 'X)^-1X 'Y,

где матрица X характеризует все независимые переменные модели. Поскольку модель имеет свободный член a₀, для которого все x_i = 1, то матрицу нужно дополнить первым столбцом, в котором все члены являются единицами, X ' - транспонированная матрица к данной, а вектор Y - вектор зависимой переменной.

Транспонируем данную матрицу:

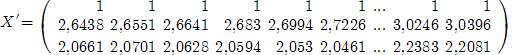
Найдем произведение транспонированной матрицы и данной:

Вычислим обратную матрицу:

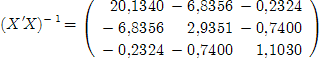
Найдем произведение транспонированной матрицы и вектора Y:

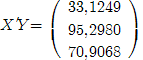
Умножив обратную матрицу на предыдущую, получим искомые коэффициенты:

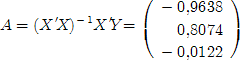
Таким образом a₀ = -0,9638, a₁ = 0,8074, a₂ = -0,0122.

Следовательно, линейная эконометрическая модель имеет вид:

Y = -0,9638 + 0,8074X₁ - 0,0122X₂.

Проверку правильности решения можно выполнить, использовав стандартную функцию Excel ЛИНЕЙН() [ЛАВ, c. 249]. Задав первым ее параметром значения диапазона Y, а вторым - диапазона X, получим аналогичный результат.

С экономической точки зрения вычисленные коэффициенты регрессии значат следующее:

- если значение фактора x₁ () изменится на 1, то показатель увеличится или уменьшится на 0,8074 ед.; - если значение фактора x₂ () изменится на 1, то показатель увеличится или уменьшится на 0,0122 ед.; Свободный член регрессии a₀ = -0,9638 указывает значение результативного признака при нулевых значениях всех факторов. Он имеет лишь расчетное значение, поскольку такой случай невозможный в реальной экономической ситуации.

Коэффициент c функции Кобба-Дугласа определяем потенцированием:

c = e^ao = e^-0,9638 = 0,1087 a = a₁ = 0,8074 b = a₂ = -0,0122

Следовательно, функция Кобба-Дугласа следующая:

Y = 0,1087·X^0,8074·P^-0,0122.

Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью коэффициентов частной эластичности, которые в случае данной двуфакторной модели они равны вычисленным коэффициентам a = 0,8074 и b = -0,0122.

Коэффициенты частной эластичности показывают, на сколько процентов изменится результативный признак, если значение одной из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.