
- •2.Поняття симультативно модел . Скорочена форма симульт моделі та способи запису.
- •3. Поняття застосування симультативних моделей. Модель попиту на товар.
- •4. Поняття застосування симультативних моделей. Модель грошової пропозиції.
- •5. Поняття застосування симультативних моделей. Модель рівноваги на ринку товарів.
- •6. Поняття застосування симультативних моделей. Модель рівноваги на ринку грошей.
- •7. Проблема ототожнення в см. Умова порядку та рангова умова ототожнення
- •8.Недоліки застосування класичного методу найменших квадратів до побудови см. Загальний огляд методів оцінювання параметрів см.
- •Метод непрямих найменших квадратів;
- •Двокроковий метод найменших квадратів;
- •9. Рекурсивні симультативні моделі та методи їх оцінювання.
- •10. Поняття дистрибутивно-лагової моделі . Причини і види лагів.
- •11. Поняття авторегресійної моделі та методи оцінювання параметрів
- •12. Суть, причини та наслідки автокореляції
- •13. Тестування автокореляції. Графічний метод.
- •14.Визначення на основі статистики Дарбіна-Уотсона
- •15.Метод Хілдрета-Лу
- •17. Суть та наслідки гетероскедастичності
- •18. Тестування гетероскедастичності. Графічний аналіз випадкових відхилень.
- •19. Суть та наслідки мультиколінеарності
- •20. Тестування наявності мультиколінеарності
- •21. Визначення рівня мультиколінеарності
- •22. Методи усунення мультиколінеарності
- •23. Метод непрямих найменших квадратів
- •24. Двокроковий метод найменших квадратів
- •25. Послідовне оцінювання параметрів дистрибутивно-лагових моделей
- •26. Модель Койка
- •27. Модель адаптивних очікувань (перша модель модифікації Койка)
- •28. Модель часткових пристусувань(друга модифікації моделі Койка)
- •29. Підхід Альмона до оцінювання параметрів дистрибутивно-лагових моделей
- •30. Тестування автокореляції. Метод рядів
- •31. Методи усунення автокореляції
- •32. Тестування автокореляції. Критерій Дарбіна-Уотсона (dw-критерій)
- •33. Тестування автокореляції. H-критерій Дарбіна-Уотсона
- •34. Метод Кохрана-Оркатта
- •35. Аналітичні методи тестування гетероскедастичності. Критерій Бартлетта
- •36. Аналітичні методи тестування гетероскедастичності. Тест рангової кореляції Спірмена
- •37.Аналітичні методи тестування гетероскедастичності. Тест Голдфельда-Квандта
- •38.Аналітичні методи тестування гетероскедастичності. Тест Парка
- •39.Аналітичні методи тестування гетероскедастичності. Тест Глейзера
- •40. Аналітичні методи тестування гетероскедастичності. Тест Годфрея
- •41. Метод зважених найменших квадратів (дисперсії випадкових величин відомі)
- •42.Метод зважених найменших квадратів (дисперсії відхилень невідомі)
- •43. Алгоритм Феррара — Глобера.
- •44. Узагальнений метод найменших квадратів (матричний підхід)
13. Тестування автокореляції. Графічний метод.
Використовують декілька варіантів графічного визначення автокореляції. Одна із них передбачає побудову так званих послідовно-часових графіків, які на площині представляють відхилення еt в моменти часуt. У цьому разі по осі абсцис відкладають або моменти часу отримання статистичних даних, або порядкові номери спостережень, а по осі ординат-відхилення еt.Можна припустити що на рисунку а-г зображають деякі зв’язки між відхиленнями, тобто між ними наявна автокореляція. Відсутність систематичності відхилень на рис. д свідчить про відсутність автокореляції.

Наприклад на рис. б, відхилення спочатку здебільшого відємні, потім додатні потім знову відємні. Це свідчить про наявність деякої залежності. Навіть більше можна сказати, що наявна додатна автокореляція випадкових відхилень. Вона стає наочнішою якщо рис. б доповнити графіком et від et-1, який у цьому разі матиме орієнтовно вигляд

Отже, здебільшого точки на цьому графіку розташовані в І іШ четвертях декартової системи координат, що підтверджує додатну залежність між сусідніми значення випадкових відхилень. Варто зазначити, що в сучасних економетричних пакетах аналітичний вираз кореляційно-регресійної моделі доповнюється графічним представленням результатів. Зіставивши графіки кореляційно-регресійної моделі та випадкових відхилень, можна висунути гіпотезу про наявність або відсутність автокореляції випадкових величин. Якщо ці графіки перетинаються рідко, то можна припустити наявність додатної автокореляції.
14.Визначення на основі статистики Дарбіна-Уотсона
Критерій
Д-У тісно пов'язаний із коеф.кореляції
між сусідніми відхиленнями
 співвідношенням:
співвідношенням:
 )
)
Тоді
оцінка
 коефіцієнта автокореляції може
дорівнювати
коефіцієнта автокореляції може
дорівнювати
 ,
тобто:
,
тобто:

Цей метод оцінювання коеф.автокореляції застосовують при великій кількості спостережень. У цьому разі оцінка параметра буде достатньо точною.
15.Метод Хілдрета-Лу
За
цим методом КРМ
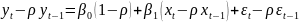 (1)
оцінюють для кожного можливого значення
з інтервалу -1;1
з деяким заданим кроком (напр.,0,001; 0,01
тощо). Величину
,
котра дає найменшу стандартну помилку
моделі (найбільший коефіцієнт
детермінації), приймають за оцінку
коефіцієнта автокореляції .
Значення
(1)
оцінюють для кожного можливого значення
з інтервалу -1;1
з деяким заданим кроком (напр.,0,001; 0,01
тощо). Величину
,
котра дає найменшу стандартну помилку
моделі (найбільший коефіцієнт
детермінації), приймають за оцінку
коефіцієнта автокореляції .
Значення
 і
оцінюють з корел-регр.моделі (1) саме із
цим значенням .
і
оцінюють з корел-регр.моделі (1) саме із
цим значенням .
Недоліком цього методу є потреба побудови достатньо великої к-ті КРМ та оцінювання їх якості (знаходження стандартної похибки моделі або значення коефіцієнта детермінації). Ітераційний метод Х.-Лу зазвичай використовують в економетричних пакетах.
Цей метод використовують тоді, коли є вважають, що автокореляція випадкових величин достатньо велика, тобто його використовують тільки для двох значень параметра : =1 та =-1.
Для динамічних рядів характерна додатна автокореляція випадкових відхилень , тому при високій автокореляції вважають, що =1. У цьому разі рівняння
(1)
можна сформулювати так:
 або
або
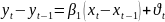 (2)
(2)
Якщо
позначити через
 ,
то залежність (2) можна записати так:
,
то залежність (2) можна записати так:
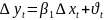 (3)
(3)
Оцінку
параметра
моделі
(3) знаходять за допомогою МНК. Оцінку
 параметра
параметра
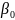 не визначають безпосередньо з КРМ, а
обчислюють за формулою:
не визначають безпосередньо з КРМ, а
обчислюють за формулою:
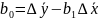 .
.
Коли
=-1,
то маємо таку КРМ:

Або (4)
(4)
Зробивши
заміну змінних
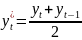 ,
,
 ,
маємо таку ПЛКРМ:
,
маємо таку ПЛКРМ:

