1. Способ полигонов

1. Уравновешивание нивелирной сети способом полигонов заключается в последовательном распределении невязок в каждом полигоне пропорционально обратным весам отдельных секций, входящих в полигон. На практике невязки распределяются пропорционально длинам секций или числу станций в них.

2. Вычисления способом полигонов производятся непосредственно на рабочей схеме сети (рис. 50). Перед вычислениями на рабочую схему наносятся: длины секций (или число станций в секциях); внутри каждого полигона нивелирной сети в специальной рамке записывается невязка этого полигона, над рамкой указывается номер данного полигона; вне полигона против секций красными чернилами наносятся длины секций полигона в долях периметра, принимая периметр за 1 или 100. Под ними чертятся рамки, в которых будут записываться столбиком поправки, приходящиеся на соответствующую секцию.

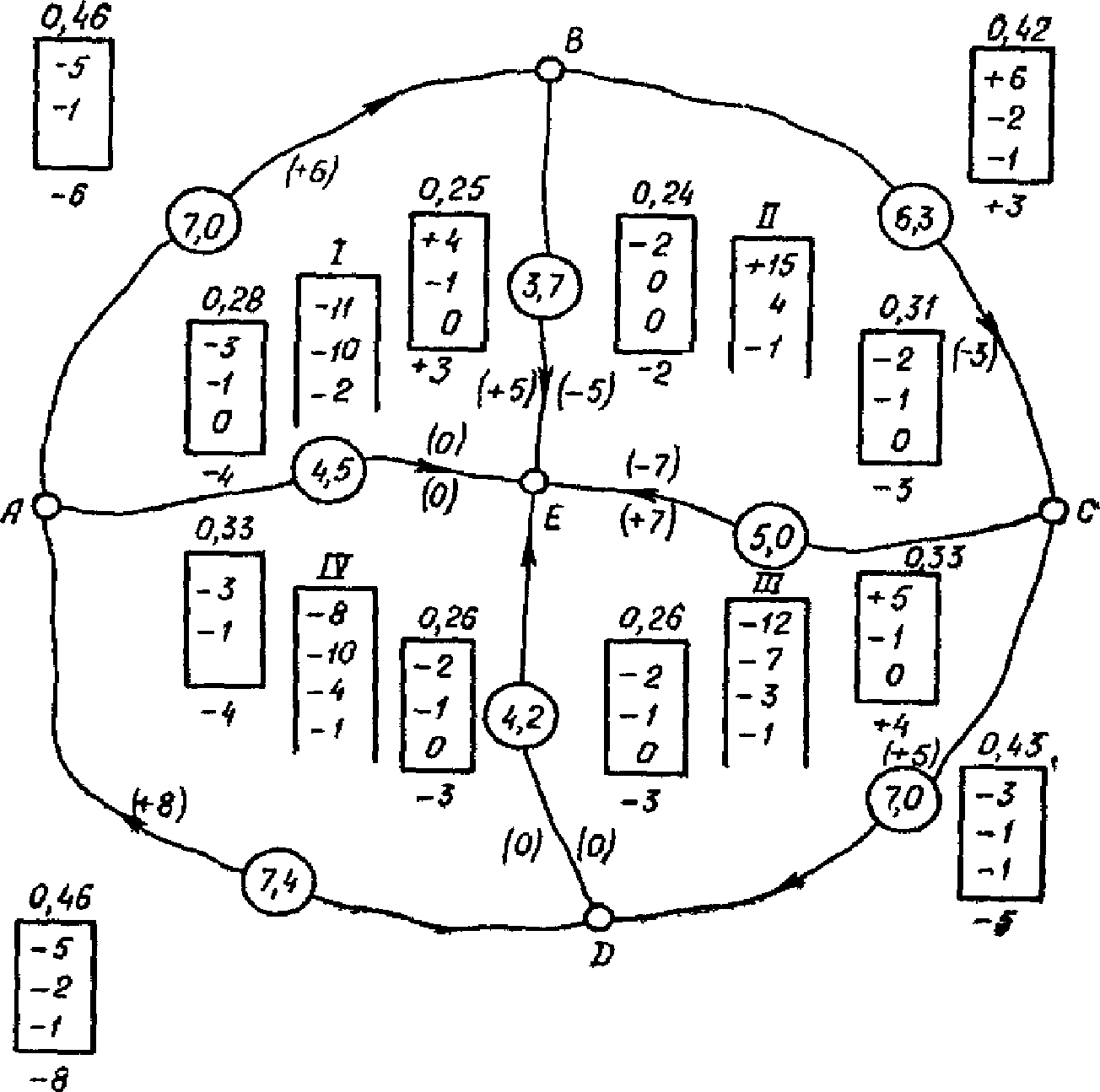
Рис. 50. Уравнивание способом полигонов

3. Распределение невязок начинается с полигона, имеющего наибольшую по абсолютной величине невязку (в нашем примере полигон II). Первый круг распределения невязок состоит из следующих этапов:

невязка (+15) полигона (II) умножается соответственно на длины секций данного полигона (красные числа вне полигона: 0,42 по секции BC, 0,33 по секции CE, 0,25 по секции BE);

полученные результаты, округленные до целых, записываются в соответствующие рамки, лежащие вне полигона, и им приписывается знак, одинаковый со знаком невязки данного полигона, таким образом найдены поправки превышений по секциям в соответствующих смежных полигонах. Сумма полученных поправок должна быть равна невязке данного полигона.

4. Затем уравнивается смежный полигон (в примере полигон III). Это уравнивание выполняется следующим образом:

Определяется остаточная невязка. Для этого невязка полигона изменяется на величину поправок в секциях, определенных из уравнивания предыдущих полигонов (в примере невязка полигона III получила поправку +5). Полученная остаточная невязка записывается в рамку невязок под предыдущей невязкой (в примере остаточная невязка полигона III - "-7").

Остаточная невязка полигона умножается соответственно на длины секций данного полигона (на красные числа вне полигона), результаты записываются в рамки, лежащие вне полигона, как описывалось выше. После завершения уравнивания полигонов по первому разу, приступают ко второму кругу уравнивания.

5. Второй круг уравнивания отличается от первого тем, что невязка в полигонах уже распределена и новая невязка получается сложением поправок, полученных в секциях полигона из первого круга уравнивания [в примере новая невязка (-4) полигона II получена путем сложения поправок по секциям CE (-2) и BE (2)].

6. Дальнейшие вычисления производятся указанным выше порядком. Закончив второй круг, переходят к третьему и т.д. Вычисления заканчиваются, когда новые поправки в секциях будут нулевыми.

7. По окончании распределения невязок в каждой прямоугольной рамке поправок вычисляют алгебраическую сумму.

8. Окончательная поправка превышения по периферийной секции (по секции, входящей только в один полигон) равна найденной сумме поправок с обратным знаком.

Эта поправка записывается в скобках внутри полигона (например по секции AB поправка равна +6).

Поправка превышения по общей секции смежных полигонов равна разности найденных сумм поправок смежных полигонов [для секции CE поправка будет равна +4 - (-3) = +7, а для EC - +4 - (-3) = +7].

9. Сумма поправок превышений секций должна равняться невязке полигона с обратным знаком.