6 Расчет открытой зубчатой прямозубой цилиндрической передачи

Рисунок 6 – Схема открытой передачи.

6.1 Исходные данные:

– момент на шестерне: Т₁ = 145,989 Нм;

– частота вращения: n₁ = 461,905 мин^-1, n₂ = 145,162 мин^-1;

– передаточное число: u = i_ОЗЦ = 3,182;

– момент на колесе: T₂ = 441,287 Нм;

– угловая скорость: ₁ = 48,346 с^-1, ₂ = 15,201 с^-1.

6.2 Материалы зубчатых колес

С учетом рекомендаций [6, §3.1] по [4, табл. 3.3] назначаем:

– для шестерни – сталь 40Х с термообработкой улучшение, , , .

– для колеса – сталь 40Х с термообработкой улучшение, , , .

6.3 Допускаемые напряжения изгиба

Базовый предел изгибной выносливости зубьев [п. 5.3.2]

Коэффициент безопасности [4, табл. 3.9]

Коэффициент, учитывающий двустороннее приложение нагрузки [4, стр. 45]

Базовое число циклов перемены напряжений и показатель степени [4, стр. 45]

;

Эквивалентное число циклов перемены напряжений [п. 5.3.2]

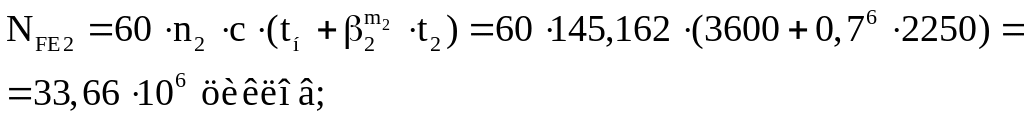
Коэффициент долговечности [4, стр. 45]

так как

Допускаемые напряжения изгиба [п. 5.3.2]

6.4 Допускаемые напряжения для проверки прочности зубьев при перегрузках.

6.4.1 Предельные допускаемые контактные напряжения [п. 5.4.1]

6.4.2 Предельно допускаемые напряжения изгиба [п. 5.4.2]

6.5 Модуль зацепления из условия изгибной выносливости [7]

где K_m = 14 – для прямозубых передач;

K_F = 1,37 – коэффициент неравномерности распределения нагрузки [4, табл. 3.7];

z₁ – число зубьев шестерни;

_bd = 0,4 – коэффициент ширины колес;

[_F] – допускаемые напряжения изгиба;

Учитывая рекомендации [п. 5.8] принимаем

Принимаем z₂ = 73.

Коэффициент формы зуба [4, с. 42; 6, табл. 4.4]

; ;

Оценка прочности зуба шестерни и колеса по отношению:

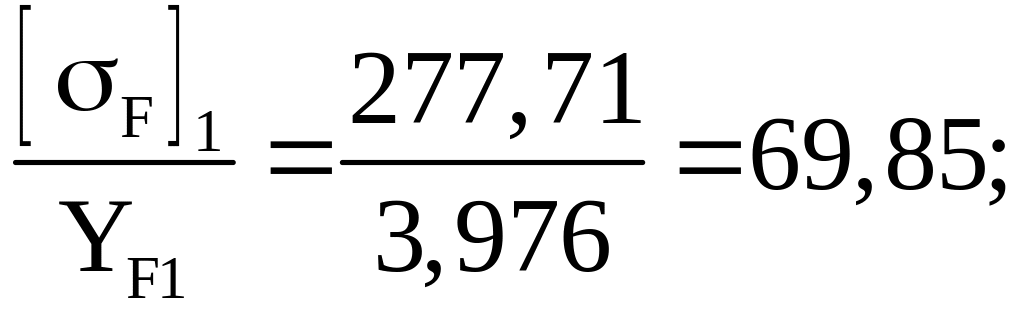
Расчет ведем по колесу, так как для него это отношение меньше.

Расчетное значение модуля зацепления

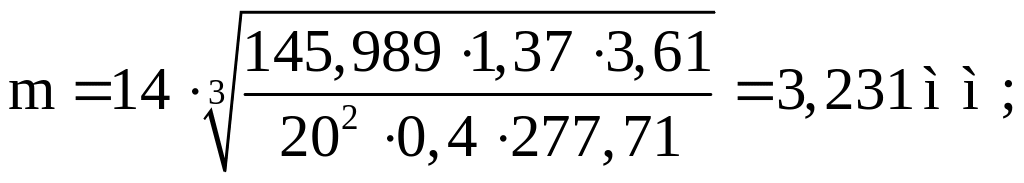
Контрольный счет на ЭВМ:

По ГОСТ 9563-60 [4, стр.36] принимаем m = 3,5 мм.

6.6 Основные геометрические размеры зубчатых колес [4, табл. 3.10]

Принимаем b_w = b₂ = 25 мм.

Принимаем b₁ = 28 мм.

мм;

6.7 Окружная скорость и степень точности изготовления [п. 6.8]

По рекомендациям [6, табл. 4.2] назначаем 9-ю степень точности изготовления.

6.8 Проверка выносливости зубьев по напряжениям изгиба

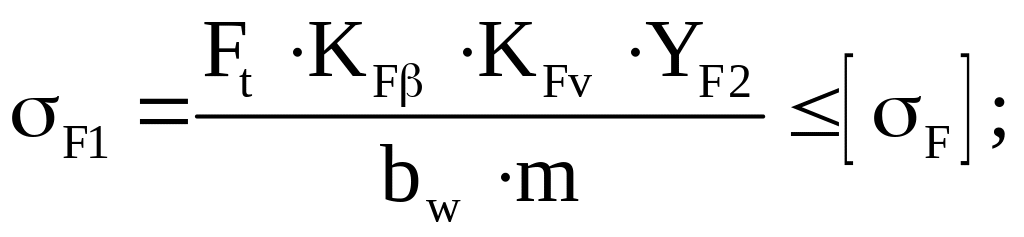
Определяем параметры, входящие в формулу.

Определяем окружную силу

Коэффициенты

;

Расчетные напряжения изгиба для зубьев шестерни и их оценка

Вывод: Выносливость зубьев по напряжениям изгиба обеспечивается.

6.9 Проверка прочности зубьев при перегрузках [3, ф. (3.4)]

где Z_H = 1,77 – безразмерный коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления [4, стр. 31];

– коэффициент, учитывающий механические свойства материала сопряженных зубчатых колес [4, стр. 31];

– расчетная окружная сила

= 0,85 – опытный коэффициент, учитывающий понижение нагрузочной способности конической прямозубой передачи по сравнению с цилиндрической;

Определяем параметры, входящие в расчетную формулу:

где K_H = 1,15 [4, табл. 3.5];

K_HV = 1,08 – коэффициент динамической нагрузки [6, табл. 4.3].

Расчетные контактные напряжения и их оценка:

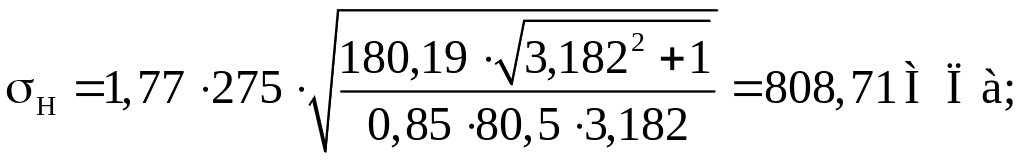
Вывод: Прочность зубьев при перегрузках обеспечивается.