§ 3.5. Проекція вектора на вісь

Означення 3.5.1. Розглянемо яку-небудь пряму у просторі та одиничний вектор (орт), паралельний цій прямій. Будемо говорити, що вектор визначає додатний напрямок на прямій. Пряму, із визначеним на ній додатним напрямком, будемо називати віссю.

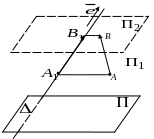
Рис. 3.2. Проекція вектора на вісь

Означення 3.5.2. Нехай – деяка вісь із ортом , – площина, яка не паралельна осі, – довільно взята точка простору. Проведемо через точку площину , що паралельна площині . Нехай – точка перетину площини з віссю . Точку будемо називати проекцією точки на вісь , яка взята паралельно площині .

Означення 3.5.3. Нехай – деякий вектор, а та – проекції його початкової та кінцевої точок на вісь , що взяті паралельно одній й тій самій площині . Вектор називається векторною проекцією вектора на вісь паралельно площини та позначається так:

.

Зрозуміло, що вектор і орт осі колінеарні. Отже, за теоремами 3.3.1 та 3.3.2

. (5.1)

Означення 3.5.4. Число з рівності (5.1) називається скалярною проекцією вектора на вісь :

.

Властивості проекцій векторів на вісь характеризують такі теореми, які приводимо без доведення.

Теорема 3.5.1 [2] Проекції двох рівних векторів та на вісь рівні: .

 

Теорема 3.5.2 [2]. Проекція суми векторів на вісь дорівнює сумі проекцій доданків

.

 

Теорема 3.5.3 [2]. Для будь-якого дійсного числа

.

 

Досі розташування площини , паралельно який знаходилися проекції векторів на вісь , вважалося довільним. При цьому, зрозуміло, виключався випадок, коли площина паралельна осі .

Означення 3.5.5. Якщо площина перпендикулярна осі , то проекції векторів на вісь називаються ортогональними (прямокутними) або просто проекціями.

Неортогональну проекцію вектора на вісь надалі будемо називати косокутною. Розташування площини відносно осі вважалося довільним у наведених вище теоремах про проекції, тому ці теореми справедливі, як для косокутних, так і для прямокутних проекцій.

Означимо поняття кута між двома напрямками, тобто кута між напрямками осей, векторів, вектора та осі.

Означення 3.5.6. Кутом між двома напрямками називається кут між ортами цих напрямків, які викладено з однієї точки. Напрямки називаються ортогональними, якщо кут між ними прямий: .

На рисунку 3.3 показано кут між двома векторами та . Орти та векторів і , як зазначено вище, потрібно відкладати з однієї точки простору. Орти та спрямовані так само, як вектори та .

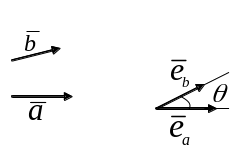
Рис. 3.3. Кут між векторами

Теорема 3.5.4 [2]. Ортогональна скалярна проекція вектора на вісь дорівнює добутку довжини вектора на косинус кута між вектором і віссю, тобто .

 

Надалі, якщо не зауважено супротивне, під проекцією вектора на який-небудь напрямок, будемо розуміти скалярну ортогональну проекцію вектора на цей напрямок.

Приклад. Знайти проекції вектора , який зображено на рисунку 3.4, на осі та прямокутної системи координат.

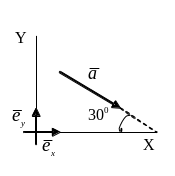
Рис. 3.4. До пошуку проекції вектора на вісь

Розв’язання. Вектор з віссю утворює кут , тому . Вектор з віссю утворює кут . Отже,

.