Лекция 5

Генерация шума турбулентным потоком. Неоднородное волновое уравнение Лайтхилла – Керла. Изотермическая струя – структура течения, турбулентные и акустические характеристики. Основные закономерности шума – мощность, направленность и спектр акустического излучения затопленной струи и струи в спутном потоке. Соосные струи.. Полуэмпирические модели шума затопленной струи, струи в спутном потоке и соосных струй.

Генерация шума турбулентным потоком

Основные источники шума в авиации имеют аэродинамическое происхождение. При этом акустическое излучение генерируется либо свободными турбулентными потоками (реактивная струя газов ГТД), либо при взаимодействии турбулентного потока с жесткими границами (шум лопаточных машин ГТД, шум обтекания планера, шум турбулентного пограничного слоя).

Впервые теоретические вопросы образования звука при движении жидкости были рассмотрены в 1877г в классической работе Рэлея «Теория звука». Попытка решения задачи о распространении звука в движущейся среде для случая безвихревого движения среды с малыми возмущениями была предпринята в 1934г Н.Н. Андреевым и И.Г. Русаковым. Первое решение задачи об источниках аэродинамического шума было получено в 1935-36 г Л.Я. Гутиным, который получил аналитическое выражение для уровня звукового давления в дальнем акустическом поле воздушного винта. В 1942 г. Е.Я. Юдин, используя методы теории подобия, установила для шума вихревого происхождения зависимость интенсивности шума от скорости обтекания твердого тела в «шестой степени». Важным шагом в изучении аэродинамических шумов явилось создание в 40-х годах прошедшего столетия Д.И. Блохинцевым теории распространения звука в движущейся среде.

В начале 50-х годов появились работа М. Лайтхилла, в которой впервые была выдвинута и использована идея акустической аналогии для решения задачи о генерации шума свободным турбулентным потоком. В конце 50-х годов Н. Керл распространил акустическую аналогию М. Лайтхилла на случай генерации звука турбулентным потоком в присутствии жестких границ. В последующем предпринимались неоднократные попытки расширить математический аппарат акустической аналогии, однако это не привело к улучшению исходной модели М. Лайтхилла в части понимания и решения проблемы шума турбулентной струи. Теория М. Лайтхилла основана на преобразовании уравнений непрерывности и сохранения импульса (уравнений Навье-Стокса) для сжимаемой жидкости при малых числах Маха в неоднородное волновое уравнение.

В рамках настоящего курса мы рассматриваем только основные положения акустической аналогии М. Лайтхилла и вывод неоднородного волнового уравнения Лайтхилла - Керла.

Уравнение Лайтхилла – Керла может быть получено на основе комбинации уравнений неразрывности и количества движения.

Уравнение неразрывности в тензорной форме имеет следующий вид:

, (5.1)

где t – время, ρ – плотность, u_i – cскорость течения потока в направлении х_i, Уравнение количества движения в тензорной форме имеет следующий вид:

, (5.2)

где F_i – сила, действующая на единицу объема среды, ρu_iu_j – тензор касательных напряжений Рейнольдса, а тензор

- тензор напряжений от сил давления и вязкости; η – коэффициент сдвиговой вязкости;

- символ Кронекера, равный 1 – при i=j, и равный 0 – при i ≠ j.

Если продифференцировать уравнение неразрывности по времени, а уравнение количества движения – по пространству (по координате х_i ) и вычесть одно из другого, то получим:

.

Прибавив и вычтя из правой части последнего соотношения выражение , получим неоднородное волновое уравнение в форме Лайтхилла – Керла:

, (5.3)

где - тензор напряжений, представляющий собой разность между напряжениями в потоке и напряжениями в однородной покоящейся среде. Учитывая сложность решения уравнения (5.3) М. Лайтхилл предложил рассматривать правую часть как эквивалентное нестационарному потоку распределение акустических источников, которые излучают звуковые волны в идеальную среду, находящуюся в состоянии покоя (акустическая аналогия).

Итак, правая часть неоднородного волнового уравнения представляет аэродинамические источники акустического излучения, а левая часть уравнения описывает распространение звуковых волн. Если в потоке имеются источники с производительностью “Q”, то в процессе изменения их производительности генерируется акустическое излучение; если имеются массовые силы, то изменение их в пространстве также является источником звуковых волн. Последний член в правой части уравнения отражает влияние тензора напряжений на генерацию звука потоком.

Общее решение уравнения (5.3) включает в себя три члена, описывающие, соответственно, источники монопольного, дипольного и квадрупольного типов, и состоит из интегралов по объему жидкости и по поверхности, обтекаемой жидкостью:

(5.4)

здесь р_i – величина аэродинамической нагрузки, действующей со стороны потока на поверхность S в направлении x_i, u_n – нормальная к поверхности составляющая скорости потока вблизи поверхности.

Отдельные составляющие решения (5.4) интерпретируются следующим образом. Объемный интеграл соответствует источникам типа квадруполь, распределенным по объему поля течения вдали от жесткой границы.

Второй интеграл описывает излучение источниками типа диполь, распределенными на обтекаемой поверхности S. Эти источники определяются пульсациями давления и вязкими напряжениями. Параметр характеризует скорость изменения импульса, которая равна нулю в случае жесткой или колеблющейся в собственной плоскости границы, а для случая перемещающейся границы этот параметр характеризует обмен количеством движения между близлежащими слоями жидкости. Параметр р_i характеризует силу воздействия потока на жесткую границу.

Третий интеграл описывает акустическое излучение источниками монопольного типа, которые расположены на поверхности S и отражают собой вытеснение среды из области пространства, обусловленное движением поверхности S. Для жестких неподвижных поверхностей нормальная составляющая скорости на поверхности u_n=0, и в этом случае монопольные источники отсутствуют. В случае мягкой (податливой) поверхности третий интеграл в решении (5.4) не равен нулю и в общем акустическом излучении потока будет присутствовать составляющая, обусловленная пульсациями вблизи поверхности нормальной к поверхности составляющей скорости потока.

При отсутствии жестких границ второй и третий интегралы в решении (5.4) отсутствуют и оно переходит в известное решение Лайтхилла, учитывающее только источники квадрупольного типа.

(5.5)

Если мгновенную скорость разложить на осредненную и пульсационную составляющие, , то есть , то сохраняя в правой части уравнения Лайтхилла (5.5) только члены, отвечающие за генерирование шума турбулентным потоком, получим соотношение (5.6), позволяющее объяснить некоторые механизмы генерации шума турбулентным потоком.

(5.6)

Первое слагаемое подинтегрального выражения содержит пространственные производные пульсационных скоростей и отвечает за взаимодействия типа «турбулентность – турбулентность». Второе слагаемое представляет собой произведение градиента средней скорости и пространственной производной пульсационной составляющей скорости и соответствует взаимодействию типа «сдвиг средней скорости – турбулентность».

В соответствии с существующей терминологией первое слагаемое определяет «собственный» шум турбулентности, а второе – «сдвиговый» шум.

В уравнении (5.5) функция источников шума T_ij определяется вторыми производными по координатами от элементов тензора полных напряжений. Тензор T_ij представляет собой разность между эффективными напряжениями в потоке и напряжениями в однородной покоящейся среде. В соответствии с акустической аналогией флуктуации плотности в турбулентной движущейся среде будут совпадать с флуктуациями плотности в невозмущенной среде, если среда находится под воздействием внешних сил T_ij.

Таким образом, точные уравнения движения жидкости могут быть записаны как как уравнения распространения звука в покоящейся среде, а действие потока можно заменить полем внешних напряжений (сил), которое воздействует на среду, вызывая в ней флуктуации плотности.

Уравнение (5.5) для фиксированной системы координат записывается в следующем виде:

(5.7)

где - координаты элемента объема жидкости dV, - координаты точки наблюдения, расположенной вне поля потока в дальнем акустическом поле, - расстояние от источника (элемента объема жидкости) до точки наблюдения. Отметим, что изменение плотности в точке поля, расположенной на удалении “r” от источника, определяется тензором напряжений “T_ij” с некоторой задержкой времени . Запаздывание обусловлено временем прохождения звуковой волны расстояния “r”. Звуковое давление вне потока определяется соотношением .

Выполнив дифференцирование в правой части уравнения (5.7), и имея ввиду, что

;

;

получим:

. (5.8)

Известно, что пульсации скорости хорошо коррелированны в близко расположенных точках пространства, и слабо коррелированны в удаленных друг от друга точках. Поэтому все поле течения жидкости можно представить состоящим из элементарных объемов, внутри которых пульсации скорости коррелированны. Флуктуации плотности, создаваемые коррелированными источниками, суммируются амплитудно, а некоррелированными источниками – суммируются энергетически, то есть складываются среднеквадратичные значения давления или интенсивности.

Допустимая величина элементарного объема жидкости определяется порядком максимально возможных изменений задержки времени в уравнении (5.8). Если в качестве характерного размера источника взять средний масштаб корреляции “ ”, то задержкой времени в пределах элементарного объема можно пренебречь. В самом деле масштаб корреляции можно рассматривать как размер типичного акустического источника, и для акустически эффективного источника он должен быть мал по сравнению с длиной волны излучаемого звука, то есть

.

Это условие выполняется при относительно низких скоростях движения среды, поскольку произведение ( ) равно характерной скорости потока. Однако если рассматривать частоту “f” в связанной с источником системе координат, то произведение ( ) можно трактовать как пульсационную составляющую скорости потока, которая не превышает величины 10%-15% от средней скорости течения, и последнее условие выполняется для всех дозвуковых течений.

Если пренебречь изменением времени запаздывания внутри элементарного объема с характерным размером “ ”, то значение подинтегрального выражения в соотношении (5.8) можно принять равным его значению в центре элементарного объема. Тогда соотношение (5.8) можно записать в виде:

. (5.9)

Поскольку для дальнего акустического поля ~ r, а в пределах самого потока

~ ,

где U – средняя скорость течения, f – характерная частота пульсаций скорости в потоке (f ~ U/ ), то :

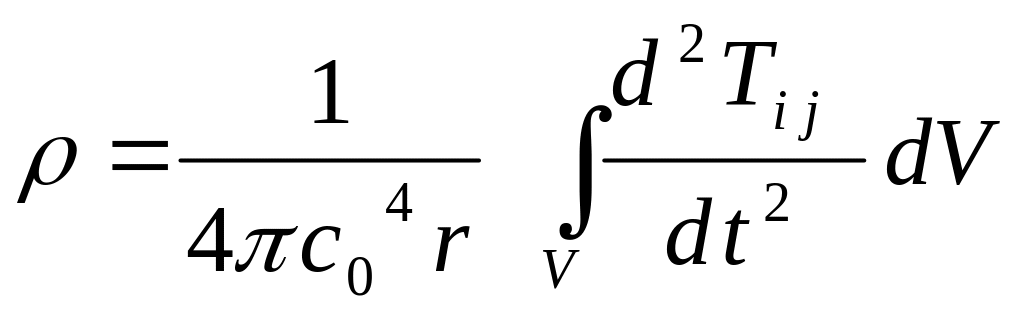~ . (5.10)

Пульсация плотности в среде вне потока, то есть в звуковой волне, пропорциональна скорости течения в четвертой степени.

Выражение для мощности акустического излучения имеет следующий вид:

(5.11)

Турбулентные характеристики дозвуковых струй

При истечении турбулентной струи в неподвижную среду на границе движущейся и неподвижной жидкости возникает так называемая поверхность тангенциального разрыва. Этот термин был введен в механику жидкости Прандтлем в 1932 г. На поверхности тангенциального разрыва, вследствие наличия поперечного градиента продольной скорости течения и потери устойчивости поверхностью, возникают вихри, беспорядочно движущиеся вдоль и поперек потока. Между соседними слоями жидкости происходит обмен конечными массами, то есть осуществляется поперечный перенос количества движения, тепла, примесей. В результате на границе движущейся и неподвижной сред формируется область конечной толщины с непрерывным распределением параметров течения в поперечном сечении потока. Эта область называется струйным турбулентным пограничным слоем.

Затопленная струя

Рассматриваются основные характеристики осредненного и пульсационного течения, которые позволяют в общих чертах представить картину развития затопленной турбулентной струи .

Затопленной называется струя, распространяющаяся в покоящейся среде. Структура затопленной дозвуковой турбулентной струи показана на рисунке 5.1

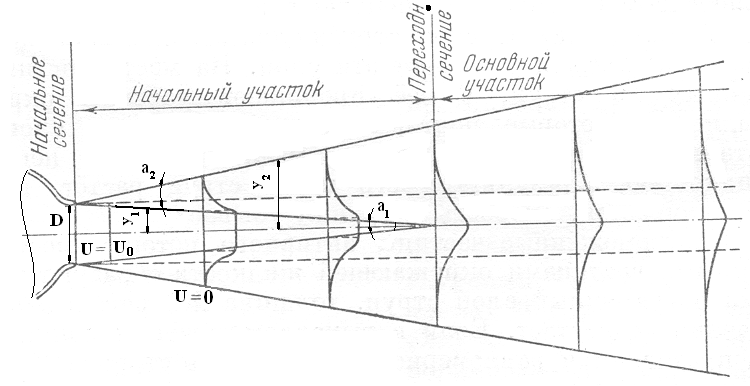
Рисунок 5.1

Схематично зону смешения затопленной турбулентной струи можно пред­ставить в виде трех участков. Между выходным сече­нием сопла и сечением, удаленным от сопла на расстояние четы­рех-пяти диаметров среза сопла, находится начальный участок течения. Он характеризуется наличием конического ядра постоянных скоростей и кольцевой конической зоны смешения, называемой пограничным слоем струи.

При равномерном поле скорости в начальном сечении затопленной струи границы ее пограничного слоя представляют собой расходящиеся поверхности, которые пересекаются у кромки сопла – в начальном сечении струи. С внешней стороны пограничный слой взаимодействует с неподвижной средой, а с внутренней стороны пограничный слой переходит в ядро постоянных скоростей. Утолщение струйного пограничного слоя приводит, с одной стороны, к возрастанию размеров поперечного сечения струи, а с другой - вызывает постепенное размывание ядра струи, области, расположенной между внутренними границами пограничного слоя.

По мере удале­ния от среза сопла ширина ядра постепенно уменьшается. Далее вниз по потоку находится переходный участок, где скорость на оси струи начинает резко умень­шаться. Остальная часть струи называется основным участком, в котором пограничный слой занимает уже все попереч­ное сечение и при удалении от сопла происходит его постоянное расширение. Вырождение профиля средней скорости по мере развития затопленной струи показано на рисунке 5.1.

Характерной особенностью свободной струи является то, что поперечные составляющие скорости в любом сечении струи малы по сравнению с продольной компонентой скорости.

Распределение средних скоростей в пограничном слое (рисунок 5.2) автомодельно (не зависит от числа Re) и аналитически может быть представлено с помощью уни­версального профиля средней скорости , где U₀ – скорость течения в ядре невозмущенного потока, Δy_c = y – y_c – расстояние от точки замера скорости до точки, в которой скорость вдвое меньше, чем в ядре, Δy_b = b ≈.y_0.9 – y_0.1 – оценка ширины зоны смешения в поперечном сечении струи как разность координат точек, в которых скорости течения равны, соответственно, 0.9 и 0.1 от значения скорости на оси струи.

Рисунок 5.2

В рамках полуэмпирической модели турбулентности Прандля принимается, что пульсация продольной составляющей скорости пропорциональна поперечному градиенту средней скорости, а величина поперечной пульсации скорости (v^’) пропорциональна пульсации продольной составляющей скорости (u^’), то есть

-v^’ ~ u^’, ,

где l – путь смешения, который принимается постоянным в поперечном сечении потока: . Прандтль принимает, что скорость нарастания пограничного слоя струи (утолщение струи) обуславливается поперечной пульсационной скоростью:

~ v^’~

Сделанные допущения приводят к линейному закону нарастания толщины затопленной струи и пути смешения в направлении течения, который хорошо согласуется с экспериментальными данными.:

const, l = c x.

Обобщение результатов исследований профилей продольной , поперечной и тангециальной составляющих пульса­ции скорости в зоне смешения начального участка струи показало, что зависимость интенсивности турбулентности от относительной поперечной координаты имеет вид, приведенный на рисунке 5.3. Максимальная интенсивность турбулентности имеет место непосредственно в следе за кромкой сопла ( ). Максимальная величина пульсации продольной составляющей скорости в начальном участке струи достигает 15%, а поперечной и тангенциальной составляющих – 10-12%. В ядре струи интенсивность турбулентности течения определяется начальной турбулентностью потока и на рисунке 5.2 составляет 2-4%.

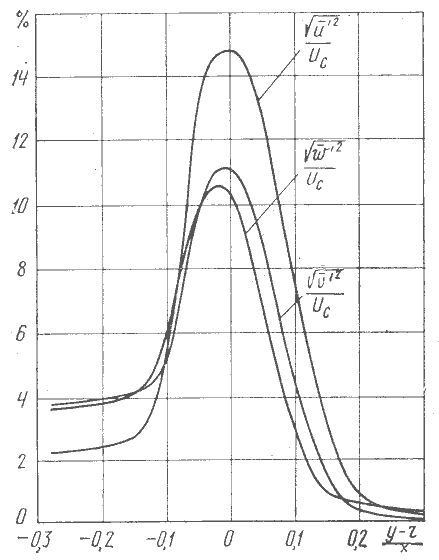
Рисунок 5.3

Спектр пульсаций скорости занимает широкий диапазон ча­стот и при анализе в 1/10-октавных полосах имеет вид кривой со слабо выраженным максимумом (рисунок 5.4).

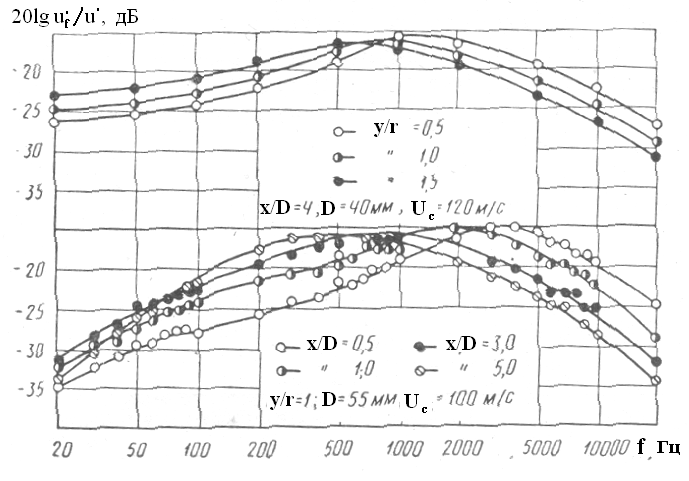
Рисунок 5.4 Третьоктавные спектры пульсаций продольной составляющей скорости в начальном участке струи

При удалении от оси струи в спектре турбулентности увеличивается доля низко­частотных составляющих. Такое же явление наблюдается и при удалении от среза сопла. Спектры пульсаций скорости на линии у/г=\, то есть в зоне максимальной интенсивности турбулентности, могут быть пред­ставлены в безразмерном виде, если в качестве безразмер­ной частоты использовать число Струхаля Sh.

В этом случае максимум спектра в 1/3-октавных полосах частот для начального и переходного участков струи соответствует числу

Sh = = 1.35,

а для основного участка

Sh = ,

где х_п – координата конца переходного участка струи.

Пространственно-временные характеристики турбулентного по­тока определяютcz на основании измерений пространственно-временных корреляционных функций или соответствующих коэффициентов корреляции . Интегральные масштабы турбулентности, которые характеризуют объем вихрей, то есть коррелированных источников звука в акустической аналогии Лайтхилла, определяются на основании измерения коэффициента корреляции: . 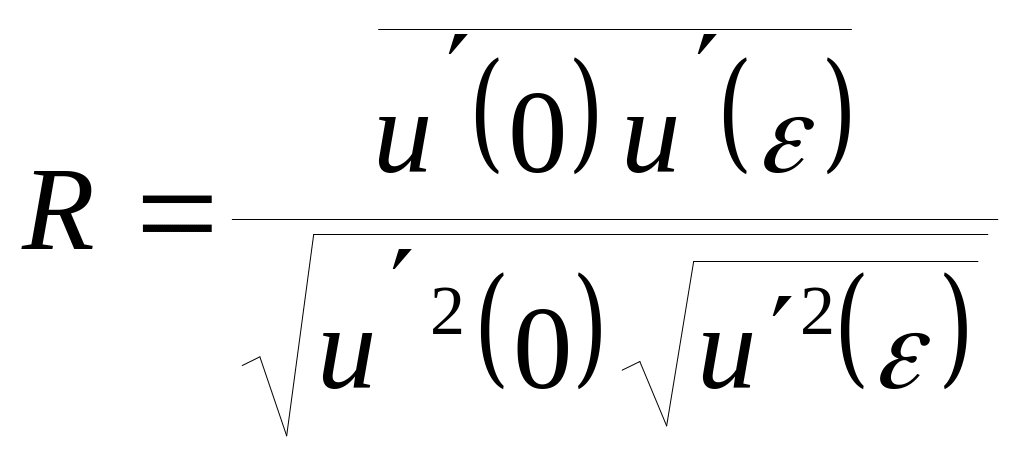Интегральные масштабы турбулентности в поперечном сечении зоны смешения струи и линейно возрастают с увеличением осевого расстояния: L_x = 0.13x, L_y = o.036x.

Скорость кон­векции турбулентных вихрей определяется на основании измере­ния пространственно-временных корреляций пульсации скорости (рисунок 5.5). При этих измерениях два датчика для измерения турбулентных пульсаций находятся на расстоянии ∆х и сигнал с одного из них задерживается на время τ. Для фиксированного расстояния ∆х получается зависимость коэффициента корреляции R, от τ. Каждая из этих зависимостей имеет максимум, соответствующий времени задержки τ_макс. Конвективная скорость турбулентности определяется соотношением .

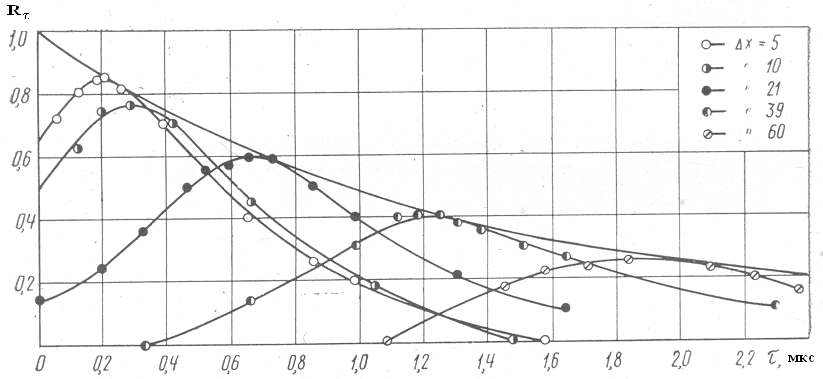
Рисунок 5.5

Установлено экспериментально, что конвективная скорость турбулентных пульсаций зависит от расположения точки измерения по сечению струи и от частоты пульсации . Скорость конвекции суммар­ных турбулентных пульсаций (в диапазоне частот 20— 20000 Гц) в зоне максималь­ной интенсивности турбулент­ности, то есть па линии у/г=1 в начальном участке струи, со­ставляет ≈ 0,5 - 0,6 от скорости истечения струи .

Струя в спутном потоке

Струей в спутном потоке называют струю, истекающую в окружающую среду, которая движется в ту же сторону, что и поток в струе.

Экспериментально установлено, что профили избыточных значений скорости, температуры и концентрации примеси в турбулентной струе, распространяющейся в спутном потоке, имеют такой же характер, как и в затопленной струе. Профили избытка про­дольной составляющей осредненной скорости хорошо согласуют­ся с универсальным профилем избыточной скорости Шлихтннга

, (5.12)

где , , U – местная средняя скорость течения, b – ширина зоны смешения, определяемая соотношением , y_0.2 и y_{0.8 –} поперечные координаты точек поля течения, в которых избыточная скорость равна, соответственно, 0.2 и 0.8.

Вместе с тем дальнобойность струи, а значит и развитие зоны смешения, зависят от интенсивности начальной турбулентности в струе и спутном потоке. Увеличение интенсивности начальной турбулентности в спутном потоке от 1,5% до 12% приводит, при значении параметра спутности m_v = U_{2 /} U₁ = 0.6, к сокращению длинны начального участка струи от 6, до 2 калибров (рисунок 5.6).

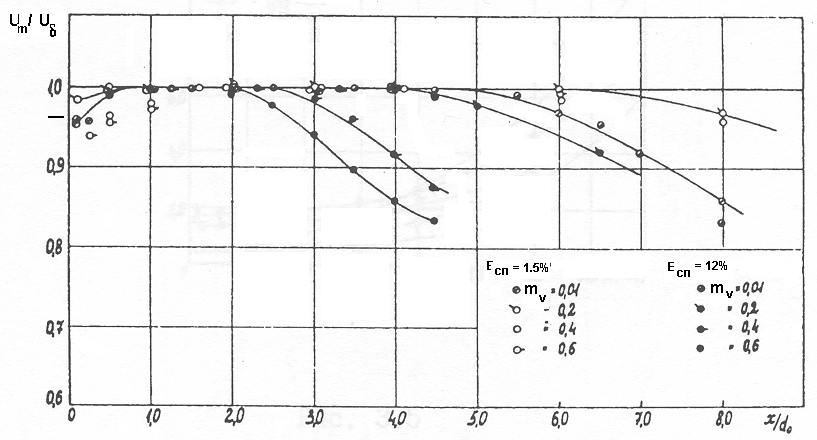
Рисунок 5.6

Скорость расширения струи в спутном потоке может быть оценена следующим образом. Скорость нарастания толщины пограничного слоя при отсутствии влияния начальной турбулентности в спутном потоке определяется только величиной поперечного градиента продольной составляющей скорости струи ( ~ ) . В этом случае закон нарастания толщины пограничного слоя имеет вид:

~ ~ ~ , (5.13)

где - степень турбулентности потока, обусловленная поперечным градиентом средней скорости, а m_v – параметр спутности. Если же спутный поток обладает заметной начальной турбулентностью, то появится дополнительное увеличение толщины пограничного слоя струи, равное

~ ~ ~ . (5.14)

При условии, что учитываемые механизмы переноса вещества поперек зоны смешения струи – градиентный и пульсационный – являются независимыми, то для ширины зоны смешения струи в турбулентном спутном потоке справедливо соотношение

, или

, (5.15)

где С, С₁=f( ) – корректирующие коэффициенты.

Соответствующие соотношения для интенсивности турбулентности в зоне смешения струи, истекающей в турбулизованный спутный поток, и для Рейнольдсовых напряжений сдвига имеют следующий вид:

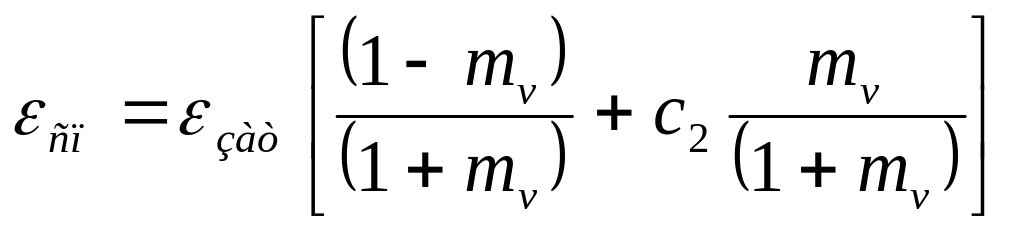, (5.16)

. (5.17)

Спутный поток оказывает сильное влияние на микроструктуру тур­булентного течения в струе: с увеличением параметра спутности интенсивность турбулентности вдали от среза сопла (но в пределах начального участка струи) уменьшается (рисунок 57). При этом максимум турбулентности и Рейнольдсовых напряжений сдвига в поперечном сечении струя распо­лагается в следе за кромкой сопла. При значения параметра смутности, близком к нулю, влияние спутного потока на турбулентность в струе имеет место лишь вблизи от среза сопла , а на удалении свыше трех калибров опытные данные совпадают с результатами измерений в затопленной струе. Влияние турбулентного следа на интенсивность продольной составляющей пульсации скорости в струе заметно лишь вблизи сопла, на расстоянии не более 2-х калибров от среза.

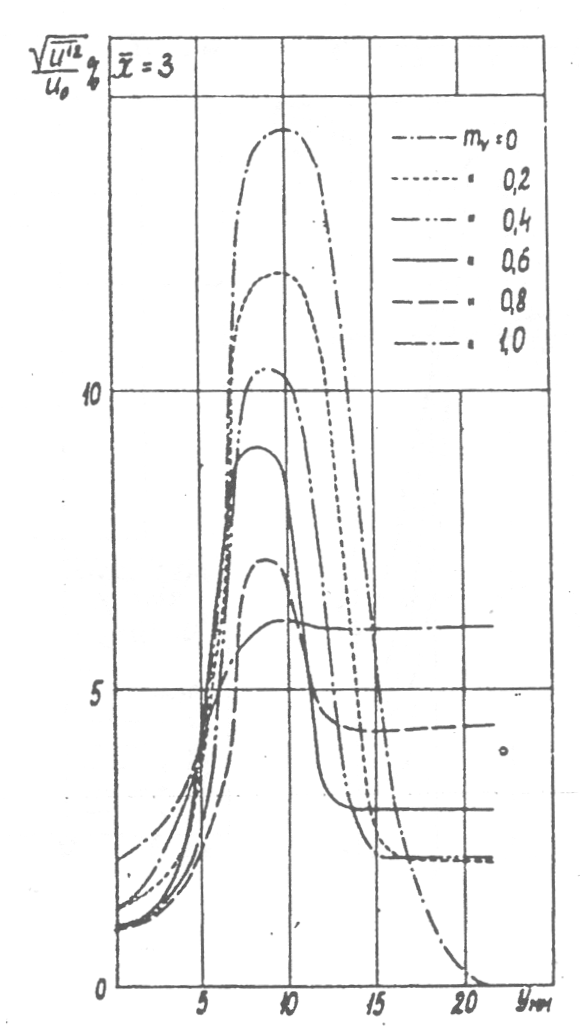
Рисунок 5.7

На рисунке 5.8 приведены результаты измерений максимальной интенсивности турбулентности (продольной и поперечной составляющих пульсаций скорости) в зоне смешения струи со спутным потоком при различных значениях параметра спутности m_v и началъной турбулентности спутного потока. Для сравнения здесь штрих-пунктирной линией показана зависимость ' а сплошной ли­нией – зависимость , где ε_зат - интенсивность пульсации скорости в затопленной струе. Влияние начальной турбулентности спутного потока на интенсивность турбулентности в зоне смешения струи может быть весьма существенным и это влияние хорошо учитывается зависимостью, включающей начальную турбулентность спутного потока.

Рисунок 5.8

Результаты опытов со струями, распространяющимися в спутном потоке с различной интенсивностью начальной турбулентности, свидетельствуют о том, что с увеличением параметра спутности интен­сивность продольной и поперечной составляющих пульсации скорости уменьшается, но не так быстро, как этого можно было бы ожидать при низкой начальной турбулентности смешивающихся потоков.

Спектральный (третьоктавный) анализ составляющих пульсаций ско­рости показывает, что, как и для затопленной струи, вид спектра любой из трех составляющих пульсации скорости сильно зависит от положения точка измерения в осевом направлении струи и слабо изменяется - в поперечном. Спутный поток качественно одинаково влияет на все составляющие пульсации скорости. С ростом параметра m_v максимумы спектров смещаются в область высоких частот. Одновременно происходит некоторое увеличение интенсивности турбулентности на низких частотах, что, возможно, связано с влиянием турбулентного следа за кромкой сопла . При увеличении интенсивности начальной турбулентности спутного потока от 5% до 12% характер трансформации спектров изме­няется. В этом случае с увеличением т_v наблюдается лишь рост интенсивности турбулентности на низких частотах.

C увеличением параметра спутности имеется тенденция к уменьшению величины коэффициента продольной и поперечной корреляции продольной составляющей пульсации скорости. Увеличение начальной турбулентности спутного потека приводит к тому, что начиная с некоторого расстояния между термонасадками дальнейшее увеличение этого расстояния вызывает относительно слабое изменение коэффициента корреляции.

На развитие струи в спутном потоке оказывают заметное влияние турбулентный след за кромкой сопла и начальная турбулентность спутного потока. В области высоких значений параметра спутности и при низкой начальной турбулентности спутного потока преобладает влияние следа, а при ε_δ >4% - влияние начальной турбулентности.

Соосные струи

Структура сосной струи рассмотрена на рисунке 5.9, где заштрихованы ядра постоянных скоростей внутренней осесимметричной и внешней кольцевой струй. Структура изотермических соосных струй определяется значением двух параметров: параметра спутности и параметра площади .

Переходный

Начальный участок Основной участок участок

Рисунок 5.9

Профили осредненной скорости, измеренные в различных поперечных сечениях соосных струй показывают, что каждый из потоков имеет ядро постоянных скоростей, протяженность которого возрастает с увеличением параметров m_v и m_F .

Все поле течения струй можно условно разделить на три участка: начальный, переходной и основной. В начальном участке течения, длина которого определяется протяженностью ядра постоянных скоростей внешней струи, можно выделить две характерные области турбулентного перемешивания, разделенные потенциальным ядром - область смешения внешней струи с окру­жающей средой и область перемешивания внешней и внутренней струй.

Профили избыточной осредненной скорости, построенные для этих областей, хорошо согласуются с профилем избыточной осредненной скорости затопленной струи (рисунок 5.10).

Это свидетельствует о том, что в пределах начального участка внешнюю струю можно рассматривать как затопленную, а внутреннюю - как струю, рас­пространяющуюся в спутном потоке.

В переходном участке тече­ния, расположенном непосредственно за начальным, безразмерные профили скоростей не совпадают с профилем Шлихтинга, вычис­ленным как для начального, так и для основного участков тече­ния.

На некотором удалении от конца начального участка поле течения соосных струй постепенно вырождается в поле течения затопленной струи. В этой области течения, называемой условно основным участком, безразмерные профили осредненной скорости подобны.

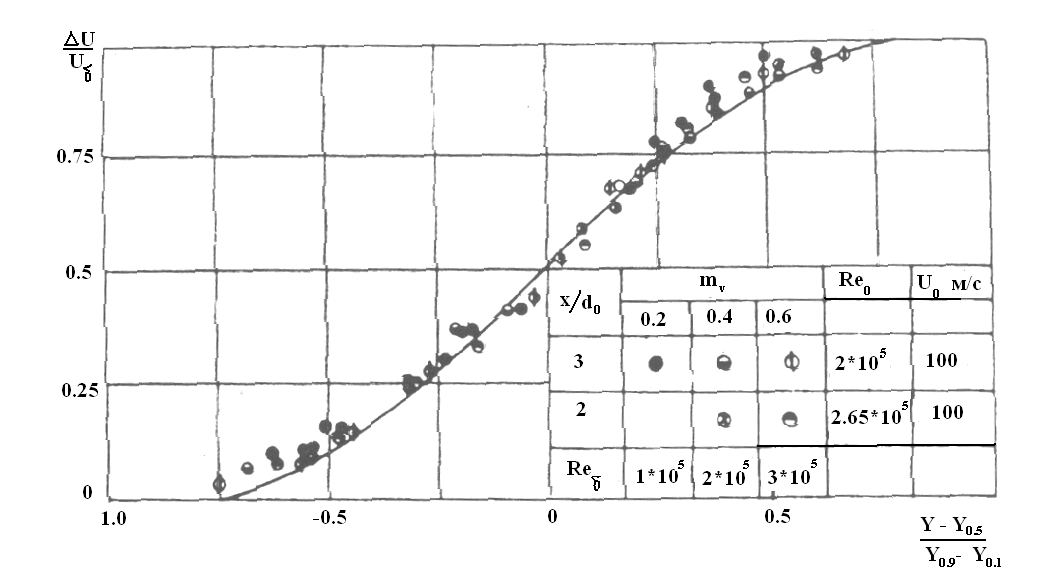
Рисунок 5.10

Таким образом, в поле течения соосных струй имеется несколько характерных областей, в которых закономерности пере­мешивания потоков соответствуют развитию зон смешения затоп­ленной струи и струи, истекающей в спутный поток. В связи с этим следует ожидать, что закономерности генерации шума этими обла­стями могут быть различными и зависеть от соотношения газоди­намических и геометрических характеристик соосных струй.

Анализ закономерности затухания осредненной скорости вдоль оси соосных струй с различными значениями параметра m_F свидетельствует о том (рисунок 5.11), что с увеличением относительных поперечных размере, внешнего потока дальнобойность внутренней струи возрастает. Так, если при m_F,=0,78 затухание осредненной скорости на оси начинается при удалении от среза на 4-5 диаметров, то есть, как у обычной затопленной струи, то при m_F =5,1 осевая скорость сохраняет пос­тоянное значение вплоть до X/d=7.

Рисунок 5.11

Исследование микроструктуры течения в начальном участке соосных струй показало, что в соответствии с наличием двух областей турбулентного перемешивания на профилях продольной составляющей пульсации скорости имеются два максимума интенсивности турбулентности (рисунок 5.12). Соотношение между интенсивностями турбулентности в зоне этих максимумов зависит от величины параметра спутности и удаления от среза сопла.

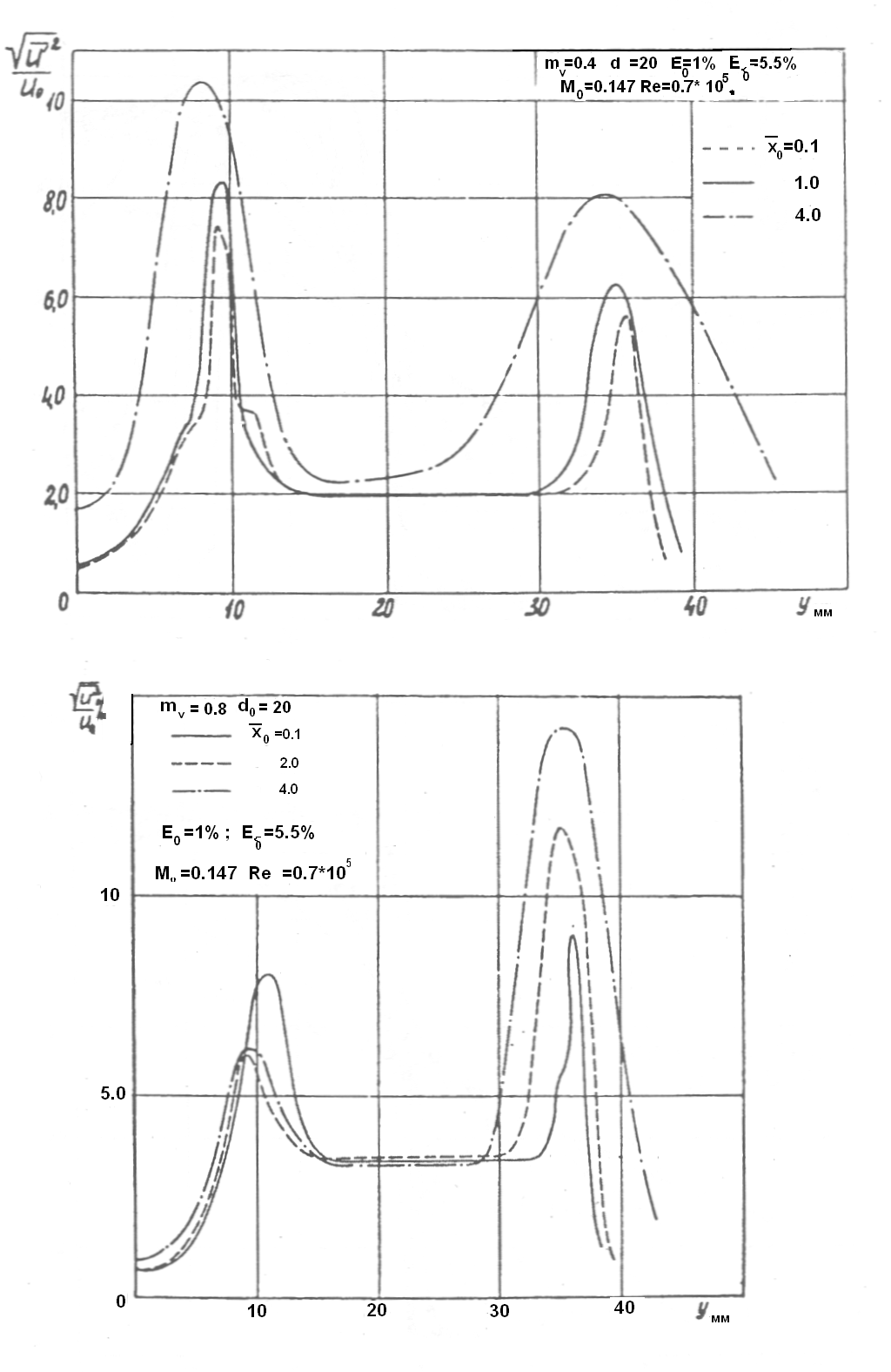
Рисунок 5.12

Измерения пространственного коэффициента поперечной корреляции между продольными составляющими пульсации скорости в различных зонах смешения начального участка соосных струй показали, что пульсации скорости во внешней области смешения не коррелироваваны с пульсациями скорости во внутренней области смешения. То есть эти области турбулентного перемешивания можно рассматривать как независимые источники акустического излучения.

Акустические характеристики струй

Затопленная струя

Важнейшими акустическими характеристиками реактивной струи являются мощность, направленность и спектр акустического излучения. Мощность акустического излучения струи пропорциональна скорости истечения в восьмой степени (5.11) и квадрату характерного геометрического размера (диаметра среза сопла) и обычно записывается в следующем виде :

, (5.18)

где: F_с – площадь поперечного сечения сопла в плоскости среза, к – коэффициент пропорциональности, величина которого получена экспериментально и при равна:

к = 0.8 10 ^-4 – для газовых струй, истекающих из дозвукового сопла,

к = 1.5 10 ^-4 – для реактивных струй ТРД при работе на взлетном и номинальном режимах,

к = 2.5 10 ^-4 – для реактивных струй ТРД при работе двигателя на режимах ниже номинального.

Значения акустической мощности реактивной струи турбореактивных двигателей представлены на рисунке 5.13 в зависимости от величины параметра Лайтхилла . При акустических испытаниях у некоторых двигателей стоял глушитель на входе в воздухозаборник, поэтому отмечается некоторый разброс экспериментальных данных. Максимальная акустическая мощность реактивной струи испытанных ТРД с тягой до 10000 кг равна примерно 100 кВт.

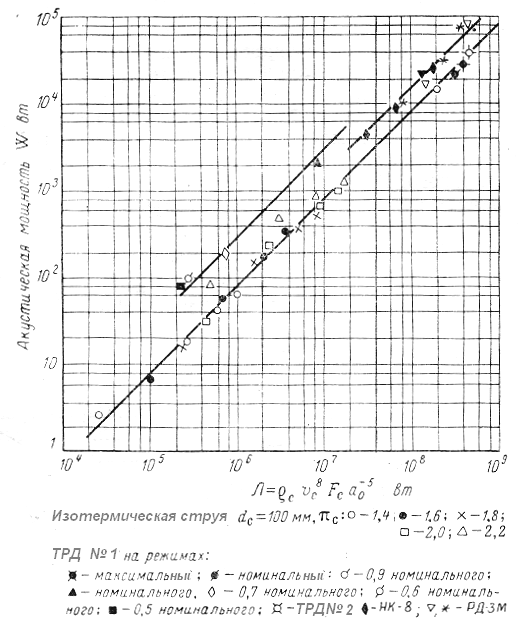
Рисунок 5.13

Значения плотности потока и скорости течения дозвуковой струи в плоскости среза конического сопла рассчитываются по газодинамическим функциям:

,

,

,

где , , = с₀ - критическая скорость звука, = - отношение теплоемкостей газа при постоянном давлении и при постоянном объеме ( =1.4 –для изотермических струй, =1.33 – для струй ТРД), R_Г – газовая постоянная (R_Г = 29.27 кГм/кГ· град – для воздуха, =29.4 кГм/кГ· град при ).

Характеристика направленности акустического излучения реактивной струи (10 lg Ф) определяется как совокупность разностей между уровнями звукового давления, измеренными в точках поля реального источника, и уровнями в тех же точках поля фиктивного источника излучения равной мощности, излучающего звук в сферу равномерно во всех направлениях.

, ,

, (5.19)

где W- мощность акустического излучения, I – интенсивность излучения, F – площадь поверхности, в которую происходит излучение, Ф – фактор направленности акустического излучения.

На рисунке 5.14 приведены экспериментальные характеристики направленности акустического излучения неизотермических реактивных струй для трех значений температуры торможения в струе, соответственно, 600⁰К, 800⁰К и 1000⁰К. Здесь угол излучения “θ” отсчитывается от оси струи.

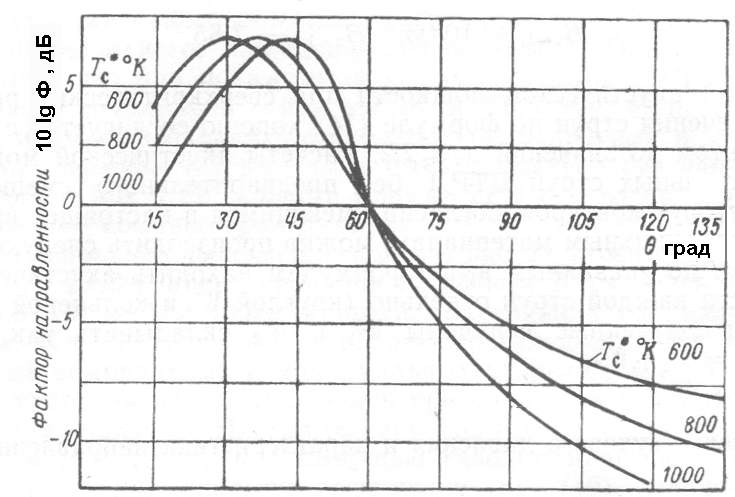
Рисунок 5.14

Максимум характеристики направленности располагается в близи оси реактивной струи, при этом с уменьшением температуры потока максимум характеристики смещается в сторону оси струи и соответствует значению θ = 30⁰ при температуре потока Т = 600⁰К.

Спектр акустического излучения реактивной струи при докритическом перепаде давления в сопле является непрерывным по частоте со слабо выраженным максимумом. При возрастании перепада давления на срезе сопла и при повышении температуры потока в спектре возрастает доля высокочастотных составляющих, а при увеличении диаметра сопла – возрастает доля низкочастотных составляющих.

На рисунке 5.15 приведен обобщенный третьоктавный спектр мощности акустического излучения модельных струй и реактивных струй ТРД в виде зависимости от числа Струхаля . Уровни спектральных составляющих акустической мощности L_Wi и уровень суммарной акустической мощности L_W связаны соотношением:

(5.20)

Рисунок 5.15

Максимум мощности акустического излучения реактивной струи имеет место на частотах, соответствующих значениям числа Струхаля 0.2 - 0.4. При этом максимальные уровни спектральных составляющих ниже уровня суммарной мощности излучения реактивной струи на 10 дБ.

Обобщенные третьоктавные спектры звукового давления реактивной струи приведены на рисунке 5.16.

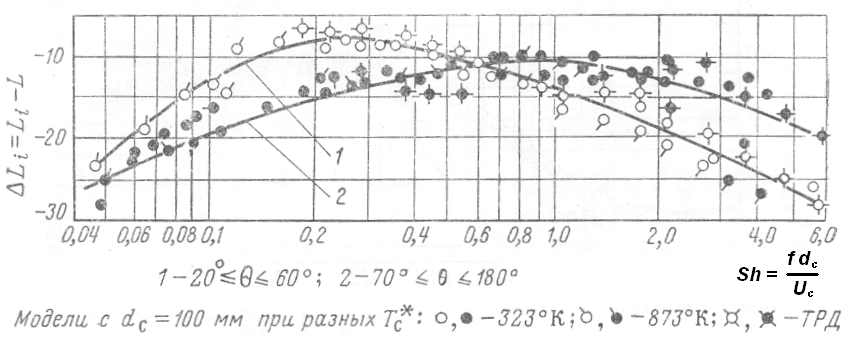
Рисунок 5.16

По оси ординат здесь отложен параметр , где L_с – суммарный по спектру уровень звукового давления, L_i - уровень звукового давления в i– й третьоктавной полосе частот.

Экспериментально установлено, что частота максимума спектра звукового давления в общем случае зависит от направления распространения акустического излучения. Вместе с тем все экспериментальные данные могут быть обобщены для двух диапазонов изменения угла излучения θ: 20⁰ < θ < 60⁰ (кривая 1 на рисунке 5.16) и 70⁰ < θ < 180⁰ (кривая 2).

В первом диапазоне направлений излучения звука спектральный максимум уровней звукового давления соответствует числам Струхаля 0.2-0.3, а во втором диапазоне направлений излучения – соответствует числам Струхаля 0.9-1.0.

Струя в спутном потоке и соосные струи

Одним из основных обобщенных параметров двухконтурного двигателя является степень двухконтурности, представляющая собой отношение расходов газа через внутренний и внешний кон­туры двигателя.

Для неизогермических соосных струй двигателя этот параметр можно записать в следующем виде:

, (5.21)

для изотермических струй:

,

здесь 1 и 2-—индексы параметров внутренней и внешней струй со­ответственно (см. рисунок 5.9), т_F — отношение площадей проходных сечений сопел внешнего и внутреннего потоков, Т-температура потока, — газодинамическая функция скорости, - газодинами­ческая функция температуры потока, т_V =U₂ / U₁ - параметр спутности в изотермических струях..

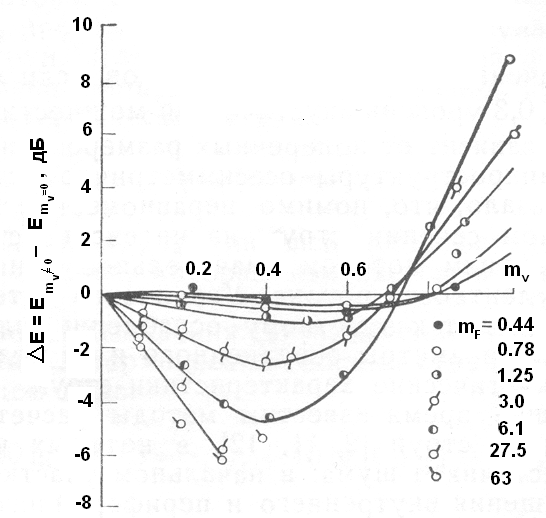
Рисунок 5.17

Влияние параметров т_F и т_V на избыточный уровень акусти­ческой мощности изотермических соосных струй рассмотрено на рисунке 5.17, где приведены результаты измерений мощности акусти­ческого излучения изотермических соосных струй. Здесь - разность между суммарными уровнями акустической мощности соосных струй и внутренней струи при отсутствии без внешней струи.

С увеличе­нием скорости истечения периферийного потока уровень акусти­ческой мощности соосных струй сначала уменьшается, а затем начинает вновь возрастать. Величина параметра спутности, при которой акустическая мощность соосных струй минимальная, зави­сит от относительных размеров периферийного потока и состав­ляет т_V = 0,4 - 0,7.

Увеличение относительных поперечных размеров периферийного потока при малых значениях параметра спутности (т_V < 0,3) приводит к снижению уровня акустической мощности соосных струй (рисунок 5.18).

Рисунок 5.18

Однако, начиная с некоторого значения параметра т_F (т_F > 20), дальнейшее увеличение поперечных раз­меров периферийного потока практически не вызывает изменения суммарной акустической мощности двух струй.

Это свидетельст­вует о том, что с акустической точки зрения внутреннюю струю можно рассматривать как струю, распространяющуюся в спутном потоке неограниченных поперечных размеров, если т_F > 20. В этом случае при т_V ≤ 0,3 уровень акустической мощности соосных струй минимален и не зависит от поперечных размеров внешнего потока.

Исследование микроструктуры осесимметричной струи в спутном потоке показало (рисунок 5.8), что, помимо неравномерности профиля ско­рости в начальном сечении струи, на интенсивность перемешива­ния струи с внешним потоком значительное влияние оказывает начальная турбулентность спутного потока. Увеличение интенсивности тур­булентности (ε_δ) приводит к заметному ослаблению влияния эффекта спутности как на параметры осредненного и пульсационного тече­ния, так и на акустические характеристики струи (рисунок 5.19).

Здесь по оси ординат отложено относительное уменьшение уровня звуковой мощности струи, распространяющейся в спутном потоке с различной начальной турбулентностью, при разных значениях параметра спутности (m_v).

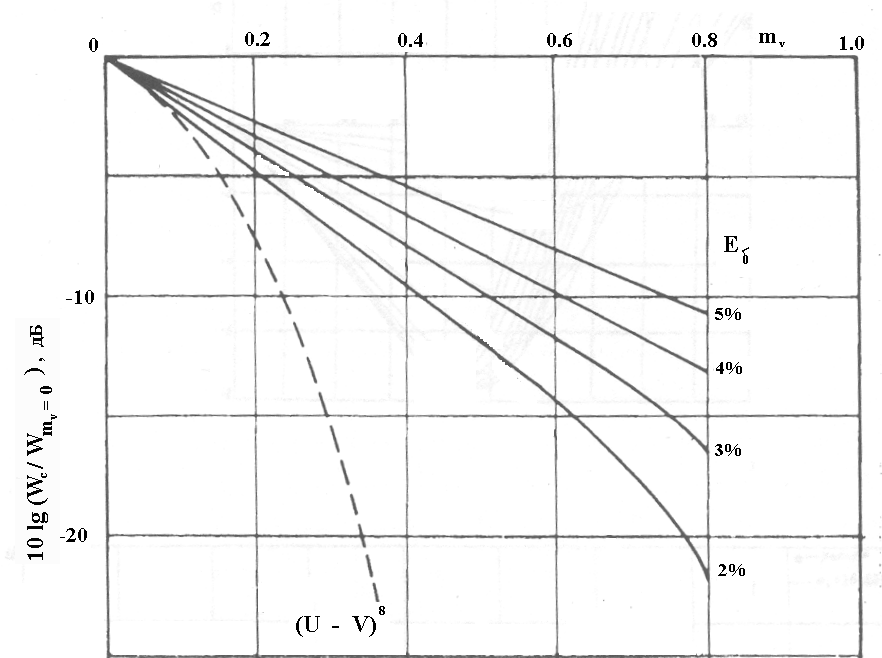
Рисунок 5.19

Для сравнения пунктиром показана зависимость (U – V)⁸, которая использовалась в ранних исследованиях для описания влияния спутного потока на мощность акустического излучения струи.

Увеличение интенсивности начальной тур­булентности спутного потока (ε_δ) приводит к возрастанию шума реактивной струи. Так при m_v =0.4 увеличение турбулентности спутного потока от 2% до 12% приводит к увеличению уровня мощности акустического излучения струи на 5 дБ (рисунок 5.19).

Характеристика направленности акустического излучения изотермической струи в спутном потоке практически совпадает с соответствующей характеристикой затопленной струи (рисунок 5.20).

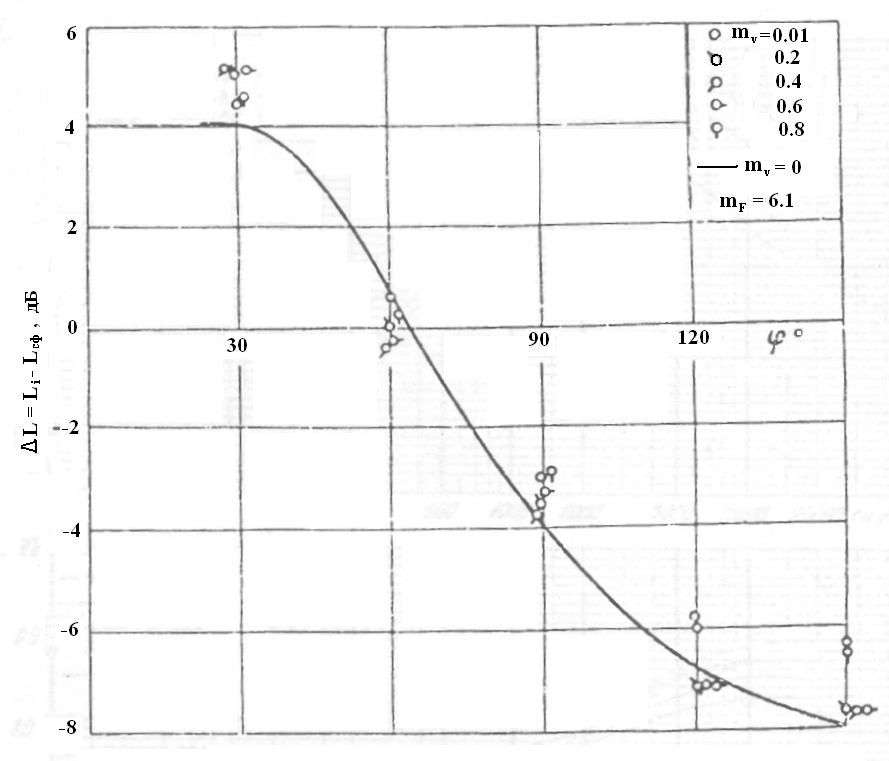
Рисунок 5.20

Влияние спутного потока на спектр шума струи рассмотрено на рисунке 5.21.

Рисунок 5.21

Полуэмпирические модели шума струй

Затопленная струя

Основу полуэмпирической модели шума затопленной реактивной струя составляют рассмотренные выше полуэмпирические графо-аналитические соотношения, определяющие мощность, направленность и спектр акустического излучения струи.

1/ Мощность акустического излучения определяется с помощью выражении (5.18), полученного с помощью метода размерностей на основе акустической аналогии Лайтхилла:

,

где: F_с – площадь поперечного сечения сопла в плоскости среза, U_с – скорость истечения реактивной струи, к – коэффициент пропорциональности, величина которого получена экспериментально и при значении плотности равна:

к = 0.8 10 ^-4 – для газовых струй, истекающих из дозвукового сопла,

к = 1.5 10 ^-4 – для реактивных струй ТРД при работе на взлетном и номинальном режимах,

к = 2.5 10 ^-4 – для реактивных струй ТРД при работе двигателя на режимах ниже номинального.

2/ Суммарный по спектру излучения уровень звукового давления (L_c) определяется по известным мощности излучения (W) и фактору направленности (10lgФ) на основе соотношения (5.19):

,

, (5.22)

где дБ – для случая излучения в сферу, и дБ – для случая излучения в полусферу. Фактор направленности акустического излучения (10lgФ) определяется с помощью обобщенной графической зависимости, приведенной на рисунке 5.14.

3/ Спектр звукового давления в третьоктавных полосах частот рассчитывается на основе обобщенных спектров звукового давления (рисунок 5.16) в соответствии с соотношением:

, (5.23)

где - спектральный уровень звукового давления в третьоктавной полосе с центральной частотой f_i в направлении θ_j , L_сj – суммарный уровень звукового давления для направления распространения звука “θ_j” , - ординаты обобщенных спектров звукового давления затопленной струи (рисунок 5.16) для частот излучения, определенных для соответствующих чисел критерия подобия – числа Струхаля .

Соотношения (5.18, 5.22, 5.23) справедливы для дозвуковых изотермических и неизотермических струй, температура торможения ко­торых не превышает 10ОО°К, а перепад давления на срезе сопла - не более 2.5.

Струя в спутном потоке

Закономерности генерации шума струей, распространяющейся в спут­ном потоке воздуха, обычно используются на практике для оценки влия­ния скорости полета самолета на интенсивность шума реактивной струи ТРД или ТРДД и в методике расчета шума реактивной струи ТРДД. От дос­товерности этих закономерностей зависит надежность методики расчета шума на местности самолетов, у которых доминирующим источником шума является реактивная струя.

Известен ряд методов оценки влияния спутного потока на интенсив­ность шума, излучаемого реактивной струей. Методы отличаются структурой расчетных соотношений. Так расчет уровня звуковой мощности струи в путном потоке производится в соответствии с зависимостями:

~ (5.24)

~ (5.25)

~ (5.26)

где U- скорость истечения реактивной струи, V - скорость спутного потока или скорость полета.

Экспериментальные исследования шума струи в спутном потоке пока­зали. что параметр (U-V) не адекватно отражает влияние спутного потока на интенсивность акустического излучения струи (рисунок 5.19). Шум затопленной струи, скорость истечения которой равна (И-V), c ростом величины " V " уменьшается значительно быстрее, нежели шум струи с постоянной скоростью истечения "U”, но распространяющейся в спутном потоке, скорость которого равна "V".

Известно, что при постоянной скорости истечения струи увеличение скорости спутного потока вплоть до значения параметра спутности практически не изменяет наклона профиля средней скорости вблизи се­редины зоны смешения; то есть величина максимального поперечного градиента продольной составляющей скорости потока слабо зависит от скорости спутного потока и, следовательно, от разности скоростей (U-V).

Снижение шума струи под влиянием спутного потока происхо­дит в первую очередь за счет уменьшения градиента средней скорости в той области зоны смешения струи, которая непосредственно примыкает к спутному потоку. Градиент скорости в этой области пропорционален разности скоростей на ее границах , а так как , то . Поэтому и влияние спутного потока на шум будет слабее, чел это следует , если использовать в оценках разность скоростей (U-V).

Ранее было показано, что акустическая мощность струи, расп­ространяющейся в спутном потоке, зависит от величины параметра спутности ( } и начальной турбулентности спутного потока (рисунок 5.19). Пос­кольку до настоящего времени практически нет данных о микроструктуре неизотермических реактивных струй, то для инженерных расчетов можно использовать следующее соотношение:

(5.27)

где m_v =1.95 - эмпирическая константа, полученная на основе резуль­татов экспериментального исследования шума изотермических струй. Соотношение при m_v =1.95 согласуется с эксперименталь­ными данными по влиянию скорости полета на шум реактивной струи ТРД.

Обобщенные характеристики направленности и спектр акустического излучения изотермической струи в спутном потоке совпадают с соответ­ствующими характеристиками затопленной струи. Нагрев затопленной струи приводит к изменению лишь характеристики направленности, а обобщен­ный спектр шума остается практически без изменения .

Анализ результатов летных испытаний самолетов с ТРДД с низкой степенью духконтурности показывает, что для неизотермической реактивной струи, распространяющейся в движущейся среде - атмосфере, имеют место ана­логичные явления. Таким образом, для расчета акустических характеристик неизотермической реактивной струи ГТД, распространяющейся в спутном потоке, получены следующие соотношения:

мощность акустического излучения:

(5.28)

суммарный уровень звукового давления

(5.29)

где фактор напрвленности " Ф - аппроксимация соответствующих экспериментальных обобщенных зависимостей.

Уровень звукового давления в i-й третьоктавной полосе частот равен:

(5.30)

, (5.31)

где - критерий Струхаля.

Соотношения (5.28-5.31) справедливы для дозвуковых изотермических и неизотермических струй, температура торможения ко­торых не превышает 10ОО°К, а перепад давления на срезе сопла - не более 2.5.

Соосные струи

В настоящее время известны различные методы расчета акустической мощности соосных струй. В некоторых методах рассматривается три основных источника шума: в начальном участке - это области смешения внутреннего и периферийного потока между собой и с окружающей средой, а в переходном и основном уча­стках - зона смешения условной осесимметричной струи, истекающей из сопла экви­валентного (при одинаковом импульсе с соосными струями) диаметра.

Акустическая мощность начального участка внешней струи и основного участка эквивалентной струи рассчитывается как для обычной затопленной струи, а акустическая мощность начального участка внутренней струи определяется как для струи в спутном потоке, то есть:

,

где - акустическая мощность внешней струи в пределах на­чального участка, - акустическая мощность внутренней струи в пределах начального участка, ^’ - акустическая мощность ос­новного участка струи эквивалентного диаметра.

При достаточно больших размерах внешней струи расчетная схема может быть упрощена, так как в этом случае отпадает необходимость в учете мощности акустического излучения струи эквивалентного диаметра. Это обстоятельство позволяет предложить более про­стую схему расчета, при которой общая акустическая мощность соосных струй представляет собой сумму мощностей акустического излучения внешней и внутренней струй. При этом периферийный поток рассматривается как затопленная струя, а внутренний поток— как струя, истекающая в спутный поток ограниченных поперечных размеров.

Соотношение для расчета акустической мощности в этом случае может быть представлено в следующем виде:

_1зат + W₂ , (5.32)

где W₁ - акустическая мощность внутреннего потока в системе соосных струй, W_1зат - акустическая мощность внутреннего потока при отсутствии внешней струи, W₂ - акустическая мощность пе­риферийного потока, - корректирующая функция. Расчет вели­чин W_1зат и W₂ проводится по известным формулам для обычной затопленной струи. Для определения значения функции может быть использовано эмпирическое соотношение, полученное для изотермических струй:

(5.33)

где , - интенсивность начальной турбулент­ности спутного потока, которая изменяется в интервале от 0,5 до 12%.

На основании соотношения (5.32) выражение для уровня акусти­ческой мощности изотермических соосных струй может быть запи­сано в следующем виде:

, (5.34)

или

(5.35)

где - избыточный уровень акустической мощности соосных струй относительно акустической мощности струи внутреннего контура, распространяющейся в невозмущенной среде. Результаты расчета уровней звукового давления изотермической соосной струи, вы­полненного на основе соотношения (5.34), хорошо согласуются с экспериментальными данными (рисунок 5.22) , полученными для струи с параметрами m_F = 2,87 и m_V = 0.25 - 1.0 во всем диапа­зоне изменения параметра спутности.

Рисунок 5.22

В экспериментах получено, что акустическая мощность неизотер­мических струй изменяется пропорционально третьей степени от­ношения термодинамических температур струи вне зоны смеше­ния и окружающей среды , то есть

, (5.36)

где и — акустические мощности неизотермической и изо­термической струй. Тогда на основе соотношений (5.33), (5.34) и (5.36) при­ближенное выражение для мощности акустического излучения неизотермических соосных струй можно записать в следующем виде:

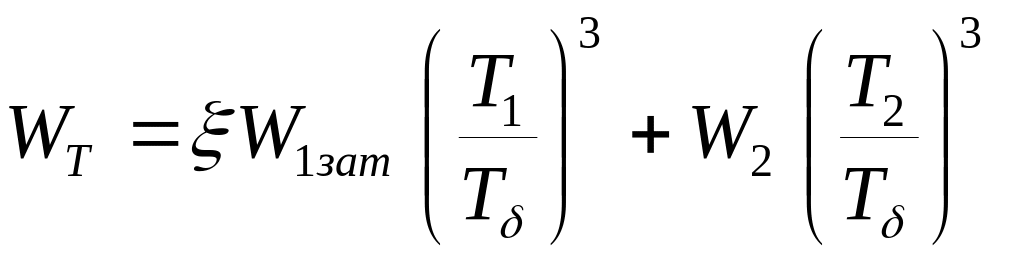. (5.37)

Соответственно для избыточного уровня акустической мощности расчетное соотношение имеет вид:

. (5.38)

Результаты расчета уровня акустической мощности реактивной струи ТРДД со степенью двухконтурности 2 и парамет­рами струи: m_F = 0.51, T₂ / T₁ = 0,43 - 0,46 и = 1, выполненного в соответствии с соотношением (5.37) для различных режимов работы двигателя, с точностью до 2 дБ совпадают с данными, полученными на основе измерений шума реактивной струи двигателя в стендо­вых условиях.

Изложенная методика расчета акустической мощности изо­термических и неизотермических соосных струй позволяет провести анализ влияния соотношений газодинамических и геометрических параметров потоков на срезе сопел на уровень суммарной акусти­ческой мощности струй. Ниже представлены результаты такого анализа, выполненного для двух различных условий: сохранения постоянства избыточного импульса внутренней струи и сохране­ния равенства тяг соосных струй и некоторой фиктивной затоп­ленной струи.

Из соотношений (5.35) и (5.38) следует, что акустическая мощность изотермических соосных струй имеет наи­меньшее значение при значении параметра m_F ,равном (рисунок 5.23):

(5.39)

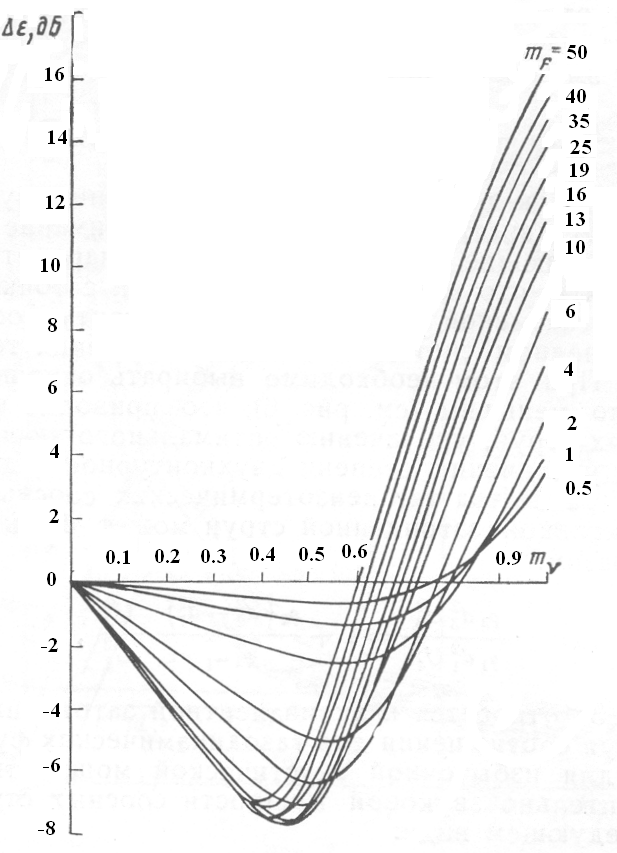
Рисунок 5.23

Значение параметра спутности, соответствующее наименьшему уровню акустической мощности изотермических соосных струй, с достаточной степенью точности может быть определено с помо­щью следующего соотношения:

. (5.40)

Величина максимального снижения шума неизотермических соос­ных струй зависит от параметров m_F , (рисунок 5.24), причем увеличение m_F и приводит к снижению шума струй, а увели­чение отношения - к возрастанию шума. Имеется оптимальное значение отношения , при котором наблюдается наиболь­шее снижение шума струи.

Рисунок 5.24

Для m_F ≤ 6 и 0.25 < < 1 соот­ветствующее эмпирическое соотношение имеет вид:

(5.41)

Возвращаясь к выражению (5.21) для степени двухконтурности газотурбинного двигателя и принимая во внимание соотношения (5.33) и (5.34), определяющие оптимальные значения параметров m_F и можно отметить, что выбор наивыгоднейшей с точки зрения сни­жения шума реактивной струи степени двухконтурности двигателя зависит, в конечном счете, от выбора отношения температур по­токов .

При этом необходимо выбирать отношение темпера­тур возможно меньшим (рисунок 5.24), что приводит к уменьшению шума соосных струй, увеличению оптимального значения парамет­ров и к увеличению степени двухконтурности двигателя.