2. Статично невизначні конструкції

Теоретичні відомості

Статично невизначними називаються конструкції, в елементах яких зусилля не можуть бути визначені тільки з рівнянь статики. Окрім рівнянь статики при вирішенні статично невизначних завдань необхідно використовувати також рівняння, що враховують деформації елементів конструкцій.

Всі статично невизначні конструкції мають так звані зайві зв'язки. «Зайвими» такі зв'язки називаються тому, що вони не є необхідними для забезпечення рівноваги конструкції і її геометричної незмінності, а обумовлені вимогами до міцності і жорсткості конструкції. Кількість зайвих невідомих, або міра статичної невизначності системи являє собою різницю між числом невідомих, що підлягають визначенню, і числом рівнянь статики.

При розрахунку статично невизначних конструкцій на міцність використовується нерівність:

де [σ] - напруга, що допускається, σ_гр - гранична напруга, [n] - нормативний коефіцієнт запасу міцності.

Умова жорсткості, як і в разі розрахунку статично визначних конструкцій, має вигляд

Згідно умовам міцності і жорсткості виділяють задачі трьох типів:

1) підбір параметрів стержня, які забезпечать роботу при заданих навантаженнях; 2) перевірка існуючої конструкції на міцність і жорсткість; 3) визначення допустимих напружень за заданим коефіцієнтом запасу.

Рекомендації до розв’язання задачі №2

1. Знаходять міру статичної невизначності n.

2. Складають рівняння рівноваги відсічених елементів конструкції, що містять невідомі зусилля (статична сторона завдання).

3. Встановлюють зв'язок між деформаціями окремих елементів конструкції, виходячи з умов спільності деформацій. Отримані рівняння називаються рівняннями сумісності деформацій (геометрична сторона завдання).

4. У рівняннях сумісності виражають деформації елементів із закону Гуку через невідомі зусилля, що діють в них (фізична сторона завдання).

5. Вирішують спільно отримані рівняння відносно шуканих невідомих зусиль (задача синтезу).

Приклад розв’язання задачі №2

Для стержня ступінчастого поперечного перерізу, закладеного по кінцях (мал. 2,а), перевірити міцність:

1) з урахуванням силового навантаження силою Р = 6кН;

2) при охолоджуванні стержня на 10ºС за умови, що сила відсутня.

Прийняти F₁ = 10 см², l₁ = 4 м, l₂ = 2 м, l₃ = 2 м, Е = 2∙10⁵ МПа, коефіцієнт теплопровідності α = 10∙10^-6 град^-1, допустиме напруження [σ] = 160 МПа.

1 ). Дана система є один раз статично невизначною: дві реакції в точках А і В і одне рівняння статики.

Мал. 2,а. Статично невизначувана система Мал. 2,б. Основна система

Виберемо основну систему, відкинувши закладення В, замінивши його вплив силою Х (мал. 2,б). Умова еквівалентності систем

З іншого боку

Мал. 3а. Епюра поздовжніх сил Мал. 3б. Епюра нормальних напружень

Підставивши перше рівняння в друге, знаходимо невідому силу

Розбиваємо конструкцію на три ділянки і визначаємо

.

Тепер будуємо епюру поздовжніх сил N (мал. 3,а).

Далі знаходимо напруження в перерізах стержня

,

, .

За отриманими результатами будуємо епюру нормальних напружень (мал. 3,б). Найбільше напруження виявилось менше допустимого [σ] = 160 МПа. Отже, міцність стержня забезпечена.

2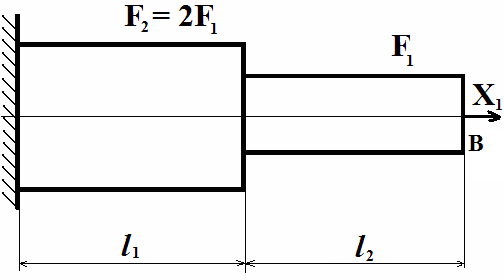 ). При розв’язанні температурної задачі виберемо основну систему, зображену на мал. 4. Умова еквівалентності систем

З іншого боку переміщення точки В повинне складатися з температурного подовження і подовження за рахунок деформації від сили Х₁.

Мал. 4. Основна система

Розбиваємо стержень на дві ділянки в місцях зміни поперечного перерізу. На кожній із ділянок поздовжня сила

М ал. 5а. Епюра поздовжніх сил Мал. 5б. Епюра нормальних напружень

За результатами розрахунків будуємо епюри N і σ (мал. 5,а і б).

Найбільше напруження виявилось менше допустимого [σ] = 160 МПа. Отже, міцність стержня забезпечена.