Модуль 4
10. Стійкість стиснутих стержнів
Теоретичні відомості
При стиску довгого тонкого стержня осьовою силою він може вийти з ладу не через те, що напруження в поперечних перерізах стануть більші за допустимі, а через те , що стержень втратить свою початкову прямолінійну форму. Для таких стержнів, окрім розрахунку на міцність, потрібно виконувати розрахунок на стійкість.
При дії на стержень стискуючої сили можна спостерігати три форми його рівноваги:
1. Стійка рівновага – при будь-якому малому відхиленні від положення рівноваги тіло повертається в початкове положення при усуненні причини, що викликала це відхилення.
2. Нестійка рівновага – після малого відхилення від початкового прямолінійного положення він не тільки не повертається в початкове положення, а й отримує додаткове переміщення.
3. Байдужа рівновага - після малого відхилення від початкового прямолінійного положення він залишається в цьому новому положенні рівноваги.
Розрахунок на стійкість повинен забезпечити роботу елементу конструкції при первинній формі його пружної рівноваги, тобто при навантаженнях, менших критичних.
Стискуюча сила, що фактично діє або допускається, має бути в деяке число разів менше критичною. Це умова стійкості прямолінійної форми рівноваги стержня може бути представлена так:
(10.1)
де Р – допустиме значення сили, що стискує; Ркр – критичне значення стискуючої сили для стержня, що розраховується; пу – заданий коефіцієнт запасу стійкості.
Критична сила обчислюється за формулою Ейлера:
(10.2)
де - коефіцієнт зведеної довжини стержня, що залежить від способу закріплення.
При втраті стійкості згин стержня відбувається в площині найменшої жорсткості. Кожен з поперечних перерізів обертається довкола тієї з головних осей, відносно якої момент інерції мінімальний, тому у формулу Ейлера входить величина Ітіп.
На мал. 35 наведені значення коефіцієнтів зведеної довжини для деяких способів закріплення стержня
М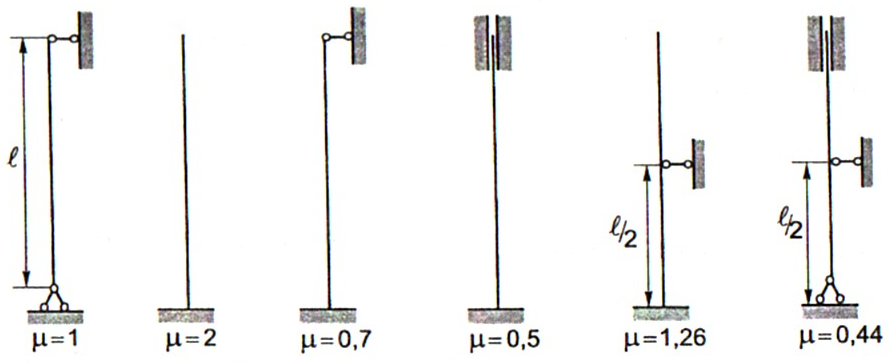
ал.
35. Способи закріплення стержня
Знайдемо критичну напругу σкр з формули Ейлера. За визначенням критичної напруги
(10.3)
З врахуванням радіусу інерції
(10.4)
для нормального напруження маємо
(10.5)
Гнучкість стержня – відношення зведеної довжини стержня до мінімального радіусу інерції його поперечного перерізу. Це безрозмірна геометрична характеристика стиснутого стержня, що характеризує його здатність до втрати стійкості. Згин стержня відбувається в площині найбільшої гнучкості
(10.6)
Максимальна гнучкість залежить лише від фізико-механічних властивостей матеріалу стержня і не залежить від його розмірів. Це постійна величина для даного матеріалу.
Використовуючи поняття гнучкості λ стержня, отримуємо остаточну формулу для критичної напруги:
(10.7)
Формула Ейлера справедлива лише в межах застосування закону Гуку, тобто за умови, що критична напруга не перевищує межі пропорційності матеріалу стержня
(10.8)
Рекомендації до розв’язання задачі №10
1. Після визначення Ітіп, F та ітіп слід перевірити гнучкість стержня і порівняти її з граничною, тобто встановити, чи правильно була застосована формула Ейлера. Якщо виявиться, що при прийнятих розмірах
то необхідно провести перерахунок.
2. Для стержнів великої гнучкості
розрахунок на стійкість ведеться по формулі Ейлера і залежність напруження від гнучкості гіперболічна (так звана гипербола Ейлера).
3. Для стержнів середньої гнучкості
розрахунок на стійкість виконують по емпіричній формулі Ф.С. Ясинського. Для них залежність напруження від гнучкості лінійна:
.
(10.12)
4. Стержні малої гнучкості
розраховуються не на стійкість, а на міцність.
В таблиці 1 Додатку приведені характеристики гнучкості для деяких матеріалів.
5. При розв’язанні задачі необхідно знати коефіцієнт поздовжнього згину. Його значення приведені в таблиці 2 Додатку.
6. Значення необхідного коефіцієнта запасу стійкості залежить в основному від призначення стержня, що розраховується, і його матеріалу. Так, для сталевих стержнів приймають:
- у будівельних конструкціях [пу] = 1,7 – 2;
- для елементів машинобудівних конструкцій, наприклад для ходових гвинтів металоріжучих верстатів [пу] = 3,5 – 5;
- для чавунних стержнів в середньому [пу] = 5;
- для дерев'яних стержнів в середньому [пу] = 3.
Приклад розв’язання задачі №10
Підібрати по сортаменту двотавровий поперечний переріз стержня довжиною 5 м, що знаходиться під дією центрального стискуючого навантаження 320 кН (мал. 36, схема закріплення III). Матеріал – Ст3. Напруга, що допускається [σ] = 160 МПа.
Визначаємо розрахункову довжину стержня:
Підбираємо поперечний переріз шляхом послідовних наближень. Перша спроба: приймаємо коефіцієнт поздовжнього згину
.
Необхідна площа поперечного перерізу
По сортаменту (табл. 3 Додатку) підбираємо двотавр №27 з площею і мінімальним радіусом інерції відповідно
;
.
Гнучкість стержня
По табл. 2 Додатку за допомогою лінійної інтерполяції
Перейдемо до другого наближення, прийнявши
Необхідна площа поперечного перерізу стержня
По сортаменту (табл. 3 Додатку) підбираємо двотавр №24а з площею і мінімальним радіусом інерції відповідно
;
Гнучкість стержня
По табл. 2 Додатку за допомогою лінійної інтерполяції
Перейдемо до третього наближення, прийнявши
Необхідна площа поперечного перерізу стержня
По сортаменту (табл. 3 Додатку) підбираємо двотавр №24 з площею і мінімальним радіусом інерції відповідно
;
Гнучкість стержня
По табл. 2 Додатку за допомогою лінійної інтерполяції остаточно знаходимо
Обчислюємо напруження
Перенапруження складає
Остаточно приймаємо для стержня двотавр №24.