Часть I. Основы измерения и количественного описания данных

ПРИМЕР

П редположим, исследователя в нашем примере (табл. 3.1) интересует, как распре­деляются ответы всех учеников до проведения тренинга. Для этого он подсчитает частоту встречаемости каждого из ответов и составит таблицу распределения час­тот (табл. 3.2). Таблица показывает, что чаще встречаются средние значения выра­женности признака и реже — крайние значения.

Таб л и ца 3.2 Таблица распределения частот

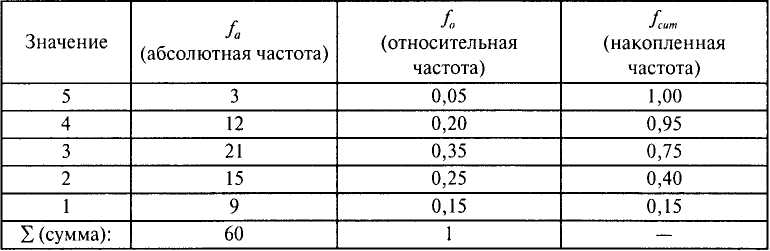
Абсолютная и относительная частоты связаны соотношением:

(3.1)

где f_a — абсолютная частота некоторого значения признака, N — число на­блюдений, /₀ — относительная частота этого значения признака. Очевидно, что сумма всех абсолютных частот равна числу наблюдений — М, а сумма всех относительных частот равна 1. Нередко относительная частота применяется для оценки вероятности встречаемости значения.

Во многих случаях признак может принимать множество различных зна­чений, например, если мы измеряем время решения тестовой задачи. В этом случае о распределении признака позволяет судить таблица сгруппированных частот, в которых частоты группируются по разрядам или интервалам значе­ний признака.

ПРИМЕР

Предположим, в группе испытуемых численностью 40 человек измерено время ре­шения тестовой задачи. Максимальное время составило 67 секунд, минимальное — 32 секунды. Построение таблицы распределения частот в этом случае производит­ся поэтапно. Построение таблицы сгруппированных частот.

1. Определение размаха: 67-32 = 35.

1. Выбор желаемого числа разрядов и интервала разрядов. Определяется произволь­ но. Обычное число разрядов — от 6 до 15. Удобным интервалом разрядов в на­ шем случае может быть 5. 35 делим на 5, получаем число разрядов — 7. Учиты­ вая, что начинать лучше с 30 или с 31 и заканчивать на 69 или 70, уточняем размах (70-30 = 40) и число разрядов (40/5 = 8).

32

ГЛАСА 3. ТАБЛИЦЫ И ГРАФИКИ

3. Определение границ разрядов. Если мы начнем с 30, то первый разряд будете 30 до 34, второй — с 35 до 49 и т. д., до восьмого — с 65 до 69. Границы соседних разрядов не должны совпадать!

4. Подсчет частот встречаемости значений признака для каждого интервала.

Табл. 3.3 содержит результат подсчета сгруппированных таким образом частот по разрядам (интервалам) значений признака — времени решения тестовой задачи.

Таблица 3.3

Таблица частот, сгруппированных по интервалам времени решения тестовой задачи

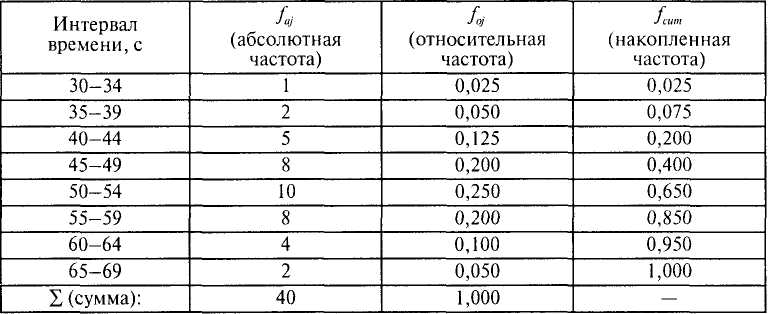
Еще одной разновидностью таблиц распределения являются таблицы рас­пределения накопленных частот. Они показывают, как накапливаются часто­ты по мере возрастания значений признака. Напротив каждого значения (ин­тервала) указывается сумма частот встречаемости всех тех наблюдений, величина признака у которых не превышает данного значения (меньше верх­ней границы данного интервала). Накопленные частоты содержатся в пра­вых столбцах табл. 3.2 и 3.3.

Для более наглядного представления строится график распределения час­тот или график накопленных частот — гистограмма или сглаженная кривая распределения.

Часть I. Основы измерения и количественного описания данных

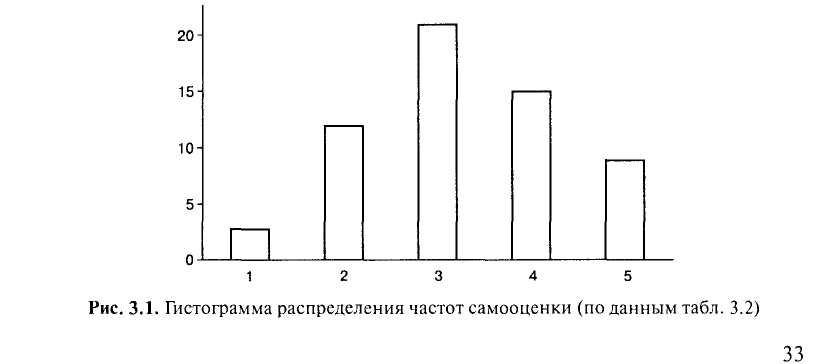
Гистограмма распределения частот — это столбиковая диаграмма, каждый столбец которой опирается на конкретное значение признака или разрядный интервал (для сгруппированных частот). Высота столбика пропорциональна частоте встречаемости соответствующего значения. На рис. 3.1 изображена гистограмма распределения частот для примера из табл. 3.2.

Гистограмма накопленных частот отличается от гистограммы распределе­ния тем, что высота каждого столбика пропорциональна частоте, накоплен­ной к данному значению (интервалу). На рис. 3.2 изображена гистограмма накопленных частот для данных табл. 3.2.

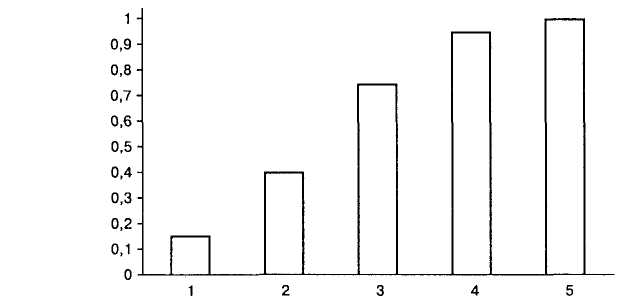
Рис. 3.2. Гистограмма накопленных относительных частот самооценки (по данным табл. 3.2)

Построение полигона распределения частот напоминает построение гис­тограммы. В гистограмме вершина каждого столбца, соответствующая часто­те встречаемости данного значения (интервала) признака, — отрезок прямой. А для полигона отмечается точка, соответствующая середине этого отрезка. Далее все точки соединяются ломаной линией (рис. 3.3).

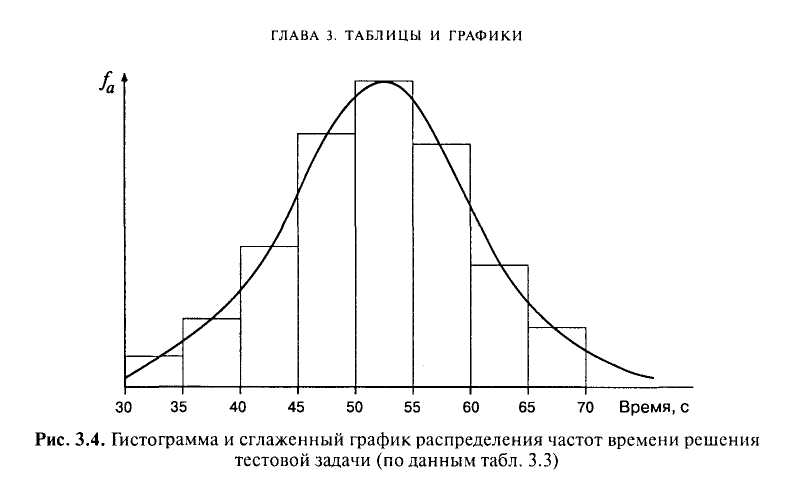
Вместо гистограммы или полигона часто изображают сглаженную кривую распределения частот. На рис. 3.4 изображена гистограмма распределения для примера из табл. 3.3 (столбики) и сглаженная кривая того же распределения частот.

34

ПРИМЕНЕНИЕ ТАБЛИЦ И ГРАФИКОВ РАСПРЕДЕЛЕНИЯ ЧАСТОТ

Таблицы и графики распределения частот дают важную предварительную информацию о форме распределения признака: о том, какие значения встреча­ются реже, а какие чаще, насколько выражена изменчивость признака. Обыч­но выделяют следующие типичные формы распределения. Равномерное распре­деление — когда все значения встречаются одинаково (или почти одинаково) часто. Симметричное распределение — когда одинаково часто встречаются край­ние значения. Нормальное распределение — симметричное распределение, у ко­торого крайние значения встречаются редко и частота постепенно повышается от крайних к серединным значениям признака. Асимметричные распределения — левосторонние (с преобладанием частот малых значений), правосторонние (с пре­обладанием частот больших значений). К понятию формы распределения мы еще не раз вернемся, прежде всего — в связи с использованием в психологии нормального распределения как особого эталона — стандарта.

Уже сами по себе таблицы и графики распределения признака позволяют делать некоторые содержательные выводы при сравнении групп испытуемых между собой. Сравнивая распределения, мы можем не только судить о том, какие значения встречаются чаще в той или иной группе, но и сравнивать группы по степени выраженности индивидуальных различий — изменчивости по данному признаку.

Таблицы и графики накопленных частот позволяют быстро получить до­полнительную информацию о том, сколько испытуемых (или какая их доля) имеют выраженность признака не выше определенного значения.