Часть I. Основы измерения и количественного описания данных

связь оказывается монотонной, то возможен переход к рангам и применение ранговых корреляций.

Довольно часто в исследованиях встречаются немонотонные связи — ког­да связь меняет свое направление (с прямого на обратное, или наоборот) при увеличении или уменьшении значений одной из переменной.

ПРИМЕРЫ

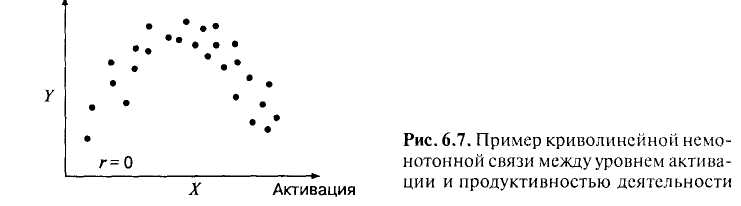
Наиболее типичный пример — это связь тревожности и результатов тестирования, или в общем случае — связь уровня активации (X) и продуктивности деятельности (Y). Связь таких переменных напоминает перевернутую (инвертированную) U (рис. 6.7). Любой из рассмотренных коэффициентов корреляции будет в этом слу­чае иметь значение, близкое к нулю.

Продуктивность

Если наблюдается немонотонная нелинейность связи, то можно поступить двояко. В первом случае сначала надо найти точку перегиба по графику рас­сеивания и разделить выборку на две группы, различающиеся направлением связи между переменными. После этого можно вычислять корреляции от­дельно для каждой группы. Второй способ предполагает отказ от применения коэффициентов корреляции. Необходимо ввести дополнительную номина­тивную переменную, которая делит исследуемую выборку на контрастные группы по одной из переменных. Далее можно изучать различия между эти­ми группами по уровню выраженности (например, по средним значениям) другой переменной.

В приведенном примере (рис. 6.7) можно по переменной «активация» выделить 3 группы (низкий, средний и высокий уровень) и далее изучать различия между этими группами по продуктивности деятельности.

КАКОЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ВЫБРАТЬ

При изучении связей между переменными наиболее предпочтительным является случай применения r-Пирсона непосредственно к исходным данным. В любом случае, обнаружена корреляция или нет, необходим визуальный ана-

88

Глава 6. Коэффициенты корреляции

лиз графиков распределения переменных и графика двумерного рассеивания, если исследователя действительно интересует связь между соответствующи­ми переменными. Применяя /•-Пирсона, необходимо убедиться, что: П обе переменные не имеют выраженной асимметрии;

• отсутствуют выбросы;

• связь между переменными прямолинейная.

Если хотя бы одно из условий не выполняется, можно попытаться приме­нить ранговые коэффициенты корреляции: r-Спирмена или х-Кендалла. Но и ранговые корреляции имеют свои ограничения. Они применимы, если:

• обе переменные представлены в количественной шкале (метрической или ранговой);

• связь между переменными является монотонной (не меняет свой знак с изменением величины одной из переменных).

Применение ранговых коэффициентов корреляции при расчете «вручную» требует предварительного ранжирования переменных. Если при этом встре­чаются одинаковые значения признаков (связи в рангах), применяется фор­мула r-Пирсона для предварительно ранжированных переменных (в случае с r-Спирмена) либо вводятся поправки на связанные ранги (в случае с т-Кен-далла).

Если есть предположение, что корреляция обусловлена влиянием третьей переменной, и все три переменные допускают применение r-Пирсона для вычисления корреляции между ними, возможна проверка этого предположе­ния путем вычисления коэффициента частной корреляции этих переменных (при фиксированных значениях третьей переменной). Если значение част­ной корреляции двух переменных по абсолютной величине заметно меньше, чем их парная корреляция, то парная корреляция обусловлена влиянием тре­тьей переменной.

Применяя коэффициенты корреляции, особое внимание следует уделять графикам двумерного рассеивания. Они позволяют выявить случаи, когда кор­реляция обусловлена неоднородностью выборки по той и другой перемен­ной. Кроме того, эти графики позволяют определить характер связи: ее линейность и монотонность. Если связь является криволинейной и не моно­тонной (например, имеет форму U), то коэффициенты корреляции не подхо­дят. 13 этом случае можно разделить выборку на группы по одной из перемен­ных, для сравнения этих групп по выраженности другой переменной.

Если обе переменные представлены в бинарной шкале (0,1), для изучения связи между ними можно применять ф-коэффициент сопряженности, если для каждой переменной количество 0 и 1 приблизительно одинаковое.

Во всех случаях, когда исследователя интересует связь между переменными, а коэффициенты корреляции для этого не подходят, изучение этой связи воз­можно при помощи сравнения групп, выделяемых по одной из переменных. Если другая переменная метрическая или ранговая, то группы сравниваются по уров­ню ее выраженности, если номинативная — то по ее распределению.

89