Часть I. Основы измерения и количественного описания данных

Часто такая «чистка» совершенно необходима. Например, при исследовании вре­мени реакции, когда основная масса наблюдений находится в диапазоне 250-700 мс, исключение нескольких «странных» значений меньше 50 мс и больше 1000 мс мо­жет существенно изменить общую картину.

По сути, наличие выбросов означает отклонение распределений одной или обеих переменных от нормального вида. В общем случае, если распределения переменных сильно скошены (асимметричны), это может существенно сни­жать значение корреляции даже при сильной связи между соответствующими свойствами или, наоборот, обусловить появление «ложной» корреляции. Осо­бенно сильно асимметричность распределений влияет на г-Пирсона. Поэто­му при существенном отклонении формы распределения хотя бы одной пере­менной от нормального вида желательно перейти к рангам и воспользоваться ранговым коэффициентом корреляции.

Влияние «третьей» переменной

Иногда корреляция между двумя переменными обусловлена не связью между соответствующими свойствами, а влиянием некоторой общей причи­ны совместной изменчивости этих переменных, которая зачастую выпадает из поля зрения исследователя. Эта общая причина может быть измерена как некоторая «третья» переменная, представленная либо в номинативной шка­ле, либо в количественной (ранговой или метрической) шкале.

Если истинная причина корреляции представляет собой номинативную пе­ременную, то это проявляется в характерной неоднородности выборки: в ней можно обнаружить различные группы, для которых согласованно меняются средние двух переменных, в то время как внутри групп эти переменные не кор­релируют. Если подобное явление возможно и существует способ содержательно интерпретируемого деления выборки на группы, необходимо вычислить кор­реляцию не только для всей выборки, но и для каждой группы в отдельности.

ПРИМЕР

Если мы возьмем достаточно большую группу людей — мужчин и женщин, то об­наружим существенную отрицательную корреляцию роста и длины волос: чем боль­ше рост, тем короче волосы. Однако, рассматривая график рассеивания роста и длины волос с выделением групп мужчин и женщин, мы обнаружим истинную при­чину этой корреляции — пол (рис. 6.6). Корреляции роста и длины волос отдельно для мужчин и отдельно для женщин будут близки к нулю.

Другой случай «ложной» корреляции — когда «третья» переменная может быть представлена в числовой шкале.

ПРИМЕР

Число церквей и количество увеселительных заведений в городах, как известно, сильно коррелируют, так же, впрочем, как рост и навык чтения у детей. Нетрудно

86

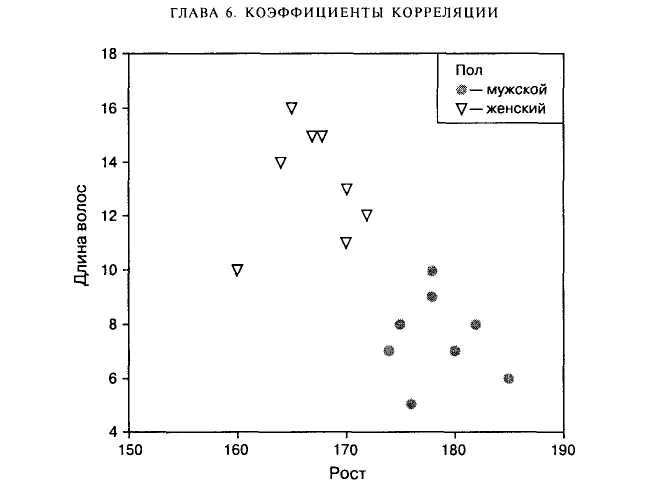
Рис. 6.6. График рассеивания для роста и длины волос. Темные точки — мужчины, светлые треугольники — женщины

догадаться, что в первом случае «третьей» переменной является численность го­родского населения, а во втором — возраст детей. (См. также пример 6.3 из раздела «Частная корреляция».)

Если истинная причина корреляции между двумя переменными Хп YИз­мерена как количественная переменная Z, то предположение о том, что имен­но она является причиной корреляции, можно проверить, вычислив частную корреляцию r_xy__z по формуле 6.5. Если частная корреляция Хп Ус учетом Z (^rxy-_z) существенно меньше г^, то весьма вероятно, что именно Zявляeтcя ис­тинной причиной корреляции Хп Y.

Следует отметить, что за редким исключением факт наличия или отсутствия корреляции может быть объяснен влиянием некоторой «третьей» переменной, упущенной из поля зрения исследователя. Таким образом, всегда остается воз­можность альтернативной интерпретации обнаруженной корреляции.

\

Нелинейные связи

Еще одним источником низкой эффективности корреляций являются воз­можный нелинейный характер связи между переменными. То, какой характер имеет связь между переменными, можно заметить, рассматривая график дву­мерного рассеивания. Это свидетельствует о важности визуального анализа свя­зи с помощью таких графиков во всех случаях применения корреляций.

К отклонениям от прямолинейной зависимости любого рода наиболее чув­ствителен коэффициент корреляции r-Пирсона. Однако если нелинейная

87