Глава 6. Коэффициенты корреляции

2. Изучается различие в агрессивности 2-х или более групп подростков, отличаю­щихся длительностью просмотра телепередач с демонстрацией сцен насилия.

Во втором примере изучение различий может быть представлено как исследование взаимосвязи 2-х переменных, одна из которых — номинативная (длительность про­смотра телепередач). И для этой ситуации также разработаны свои коэффициенты корреляции.

Любое исследование можно свести к изучению корреляций, благо изобре­тены самые различные коэффициенты корреляции для практически любой исследовательской ситуации. Но в дальнейшем изложении мы будем разли­чать два класса задач:

П исследование корреляций — когда две переменные представлены в чис­ловой шкале;

□ исследование различий — когда хотя бы одна из двух переменных пред­ставлена в номинативной шкале.

Такое деление соответствует и логике построения популярных компьютер­ных статистических программ, в которых в меню Корреляции предлагаются три коэффициента (/--Пирсона, r-Спирмена и х-Кендалла), а для решения других исследовательских задач предлагаются методы сравнения групп.

ПОНЯТИЕ КОРРЕЛЯЦИИ

Взаимосвязи на языке математики обычно описываются при помощи фун­кций, которые графически изображаются в виде линий. На рис. 6.1 изобра­жено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная. Если увеличение одной перемен­ной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функ­ция — монотонная; в противном случае функцию называют немонотонной.

Функциональные связи, подобные изображенным на рис. 6.1, являются иде-ализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погреш­ностей измерения и пр.

65

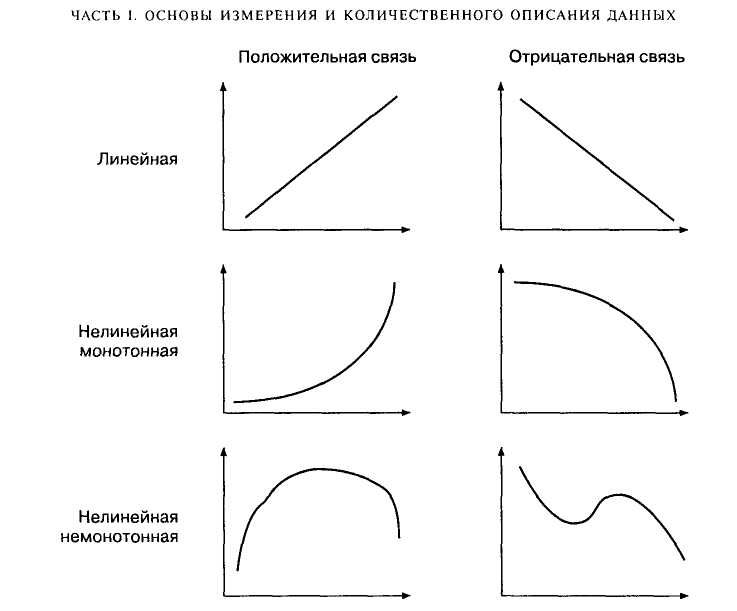
Рис. 6.1. Примеры графиков часто встречающихся функций

В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество воз­можных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значе­ний другой переменной (и наоборот). Простейшим примером является соотно­шение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной — идеальной математической функции, даже при всех ухищрениях исследова­теля по учету стройности или полноты испытуемых. (Вряд ли на этом основа­нии кому-то придет в голову отрицать факт наличия строгой функциональ­ной связи между длиной и весом тела.)

Итак, в психологии, как и во многих других науках, функциональная вза­имосвязь явлений эмпирически может быть выявлена только как вероятно­стная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания — график, оси которого со­ответствуют значениям двух переменных, а каждый испытуемый представля­ет собой точку (рис. 6.2). В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.

66

X

Рис. 6.2. Примеры диаграмм рассеивания и соответствующих коэффициентов корреляции

Коэффициент корреляции — это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапа­зоне от-1 до +1.

Сила связи достигает максимума при условии взаимно однозначного соот­ветствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью. Показателем силы связи явля­ется абсолютная (без учета знака) величина коэффициента корреляции.

Направление связи определяется прямым или обратным соотношением зна­чений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь на­зывается прямой (положительной); если возрастанию значений одной пере­менной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи являет­ся знак коэффициента корреляции.

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ г-ПИРСОНА

r-Пирсона (Pearson r) применяется для изучения взаимосвязи двух метричес­ких переменных, измеренных на одной и той же выборке. Существует множество ситуаций, в которых уместно его применение. Влияет ли интеллект на успе­ваемость на старших курсах университета? Связан ли размер заработной пла­ты работника с его доброжелательностью к коллегам? Влияет ли настроение

67