Глава 5. Нормальный закон распределения и его применение

Табл ица 5.1 Тестовые нормы — таблица пересчета «сырых» баллов в стены

Стены	1	2	3	4	5	6	7	8	9	10
«Сырые» баллы	<11	11-13	14-16	17-19	20-22	23-25	26-28	29-31	32-34	>34

Пользуясь этой таблицей тестовых норм индивидуальный результат («сырой» балл) переводят в шкалу стенов, что позволяет интерпретировать выраженность измеря­емого свойства.

В общем случае границы интервалов определяются по формуле г-преоб-разования:

K/f с/ .— A/f /т

о\

z = -

о\

где Xj — искомая граница интервала «сырых» оценок, st_t — граница интервала в стандартной тестовой шкале, М_х, о_х, M_sh o_sl — средние и стандартные откло­нения «сырых» оценок (х) и стандартной шкалы (st).

Эмпирическая нормализация применяется, когда распределение «сырых» баллов отличается от нормального. Она заключается в изменении содер­жания тестовых заданий. Например, если «сырая» оценка — это количе­ство задач, решенных испытуемыми за отведенное время, и получено рас­пределение с правосторонней асимметрией, то это значит, что слишком большая доля испытуемых решает больше половины заданий. В этом случае необходимо либо добавить более трудные задания, либо сократить время решения.

Нелинейная нормализация применяется, если эмпирическая нормализа­ция невозможна или нежелательна, например, с точки зрения затрат вре­мени и ресурсов. В этом случае перевод «сырых» оценок в стандартные про­изводится через нахождение процентильных границ групп в исходном распределении, соответствующих процентильным границам групп в нор­мальном распределении стандартной шкалы. Каждому интервалу стандарт­ной шкалы ставится в соответствие такой интервал шкалы «сырых» оценок, который содержит ту же процентную долю выборки стандартизации. Вели­чины долей определяются по площади под единичной нормальной кривой, заключенной между соответствующими данному интервалу стандартной шкалы г-оценками.

Например, для того чтобы определить, какой «сырой» балл должен соот­ветствовать нижней границе стена 10, необходимо сначала выяснить, какому г-значению соответствует эта граница (z = 2). Затем по таблице нормального распределения (приложение 1) надо определить, какая доля площади под нормальной кривой находится правее этого значения (0,023). После этого определяется, какое значение отсекает 2,3% наибольших значений «сырых» баллов выборки стандартизации. Найденное значение и будет соответство­вать границе 9 и 10 стена.

57

Часть I. Основы измерения и количественного описания данных

ПРИМЕР

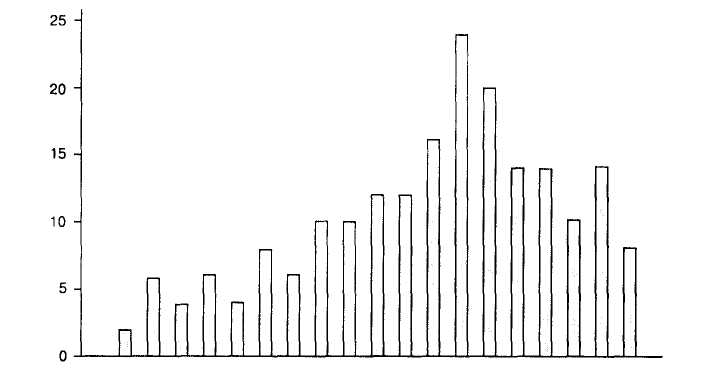
Р ассмотрим пример нелинейной нормализации. Допустим, разрабатываемый тест предполагает решение 20 заданий. Объем выборки стандартизации N= 200 чело­век. Сначала строится таблица распределения частот «сырых» оценок (табл. 5.2).

Таб л и ца 5.2

			Таблица распределения частот								«сырыхх		» оценок
Оценка	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Частота	2	6	4	6	4	8	6	10	10	12	12	16	24	20	14	14	10	14	8

Исходное распределение заметно отличается от нормального — оно имеет право­стороннюю асимметрию (рис. 5.6). В качестве стандартной выберем шкалу стенай-нов, для каждой градации которой известны процентные доли (см. рис. 5.5). Исхо­дя из этих процентных долей и таблицы распределения «сырых» оценок строится таблица тестовых норм (табл. 5.3). Сначала отбираются 4% испытуемых, решив­ших наименьшее количество заданий. У нас 8 испытуемых (4%) решили менее 4 за­даний. Это число заданий будет соответствовать 1 -му стенайну. Второму стенайну будет соответствовать результат следующих 7% (14) испытуемых: от 4 до 6 заданий, и т. д. Итог нелинейной стандартизации — таблица перевода «сырых» оценок в шкальные, стенайны (табл. 5.3).

Табл и ца 5.3 Пример нелинейной нормализации: пересчет «сырых» оценок в шкалу стенайнов

Стенайны	1	2	3	4	5	6	7	8	9
%	4	7	12	17	20	17	12	7	4
«Сырые» оценки	<4	4-6	7-9	10-12	13-14	15-16	17-18	19	20

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Рис. 5.6. Распределение «сырых» оценок (по данным табл. 5.2)

Изложенные основы психодиагностики позволяют сформулировать мате­матически обоснованные требования к тесту. Тестовая методика должна со­держать:

58