Глава 5. Нормальный закон распределения и его применение
ляется метрической — точнее, равных интервалов. Если это не так, то свойство удалось отразить в лучшем случае — в шкале порядка. Естественно, что большинство стандартных тестовых шкал являются метрическими, что позволяет более детально интерпретировать результаты тестирования — с учетом свойств нормального распределения — и корректно применять любые методы статистического анализа. Таким образом, основная проблема стандартизации теста заключается в разработке такой шкалы, в которой распределение тестовых показателей на выборке стандартизации соответствовало бы нормальному распределению.
Исходные тестовые оценки — это количество ответов на те или иные вопросы теста, время или количество решенных задач и т. д. Они еще называются первичными, или «сырыми» оценками. Итогом стандартизации являются тестовые нормы — таблица пересчета «сырых» оценок в стандартные тестовые шкалы.
55
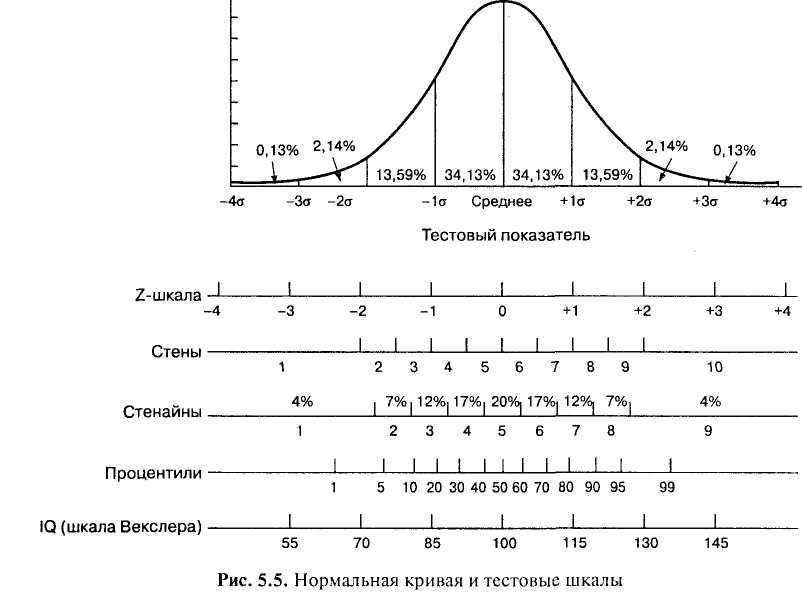
Существует множество стандартных тестовых шкал, основное назначение которых — представление индивидуальных результатов тестирования в удобном для интерпретации виде. Некоторые из этих шкал представлены на рис. 5.5. Общим для них является соответствие нормальному распределению, а различаются они только двумя показателями: средним значением и масштабом (стандартным отклонением — о), определяющим дробность шкалы.
Часть I. Основы измерения и количественного описания данных
Общая последовательность стандартизации (разработки тестовых норм — таблицы пересчета «сырых» оценок в стандартные тестовые) состоит в следующем:
определяется генеральная совокупность, для которой разрабатывается методика и формируется репрезентативная выборка стандартизации;
по результатам применения первичного варианта теста строится рас пределение «сырых» оценок;
проверяют соответствие полученного распределения нормальному за кону;
если распределение «сырых» оценок соответствует нормальному, про изводится линейная стандартизация;
если распределение «сырых» оценок не соответствует нормальному, то возможны два варианта:
перед линейной стандартизацией производят эмпирическую норма лизацию;
проводят нелинейную нормализацию.
Проверка распределения «сырых» оценок на соответствие нормальному закону производится при помощи специальных критериев, которые мы рассмотрим далее в этой главе.
Линейная стандартизация заключается в том, что определяются границы интервалов «сырых» оценок, соответствующие стандартным тестовым показателям. Эти границы вычисляются путем прибавления к среднему «сырых» оценок (или вычитания из него) долей стандартных отклонений, соответствующих тестовой шкале. Пример, приведенный ниже, демонстрирует процедуру линейной стандартизации.
ПРИМЕР
Предположим, получено распределение «сырых» оценок, соответствующее нормальному, со средним Мх = 22 и стандартным отклонением ох= 6. В качестве стандартной тестовой шкалы выбрана 10-балльная шкала стенов, предложенная Р. Кет-телом {Mst = 5,5; osl = 2). Результатом линейной стандартизации должна являться таблица пересчета из шкалы «сырых» оценок в шкалу стенов. Для этого каждому стандартному значению ставится в соответствие интервал «сырых» оценок. Границы интервалов определяются следующим образом. Среднее «сырых» оценок должно делить шкалу стенов ровно пополам (1—5 — ниже среднего, 6—10 — выше среднего). Следовательно, среднее «сырых» оценок Мх = 22 — это граница стенов 5 и 6. Следующая граница справа — отделяющая стены 6 и 7 — отстоит от среднего на as,/2. Этой границе должна соответствовать граница «сырых» оценок Мх + ох/2 = 22 + 3 = 25. Так же определяются границы всех оставшихся интервалов, а границы крайних интервалов остаются открытыми. Результатом являются тестовые нормы — таблица пересчета «сырых» баллов в стандартные тестовые оценки (табл. 5.1)1.
1 Обратите внимание, что левая граница каждого диапазона «сырых» оценок исключает границу интервалов, а правая — включает ее. Можно было бы сделать и наоборот, но главное, чтобы границы соседних диапазонов не совпадали, во избежание недоразумений при попадании индивидуального значения на границу интервалов.
56