Часть I. Основы измерения и количественного описания данных

Л

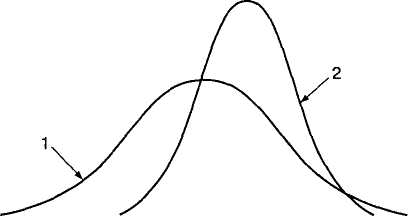
Общительность

Рис. 4.3. Графики распределения относительных частот общительности юношей (1) и девушек (2)

ОБРАБОТКА НА КОМПЬЮТЕРЕ

Способ 1. Выбираем Analyze > Descriptive Statistics > Frequencies... В открыв­шемся диалоговом окне (Frequencies) переносим из левой в правую часть ин­тересующие нас переменные. Если таблица распределения частот нас не ин­тересует, снимаем флажок Display frequency tables (Показывать таблицы частот). Нажимаем кнопку Statistics... Выбираем интересующие нас статистики и от­мечаем их флажком: центральной тенденции (Central Tendency) — среднее (Mean), моду (Mode), медиану (Median); изменчивости (Dispersion) — стан­дартное отклонение (Std. deviation), дисперсию (Variance); распределения — асимметрию (Skewness) и эксцесс (Kurtosis). После этого нажимаем Continue, затем ОК и получаем результат.

Способ 2. Выбираем Analyze > Descriptive Statistics > Descriptives... В от­крывшемся диалоговом окне переносим из левой в правую часть интересую­щие нас переменные. Нажимаем кнопку Options... и отмечаем флажком те статистики, которые нас интересуют (см. выше). Нажимаем Continue, затем ОК и получаем результат.

Глава 5

НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ

Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.

История применения закона нормального распределения в социальных и биоло­гических науках начинается, по-видимому, с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как про­должительность жизни, возраст вступления в брак и появления первого ребенка и т. д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встре­чаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые от­клонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. Эту закономерность он назвал «законом уклонения от средней величины». В его исследованиях, и позднее — в исследованиях англичанина Ф. Галь-тона, было доказано, что распределение частот встречаемости любого демографиче­ского (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большой выборке людей, имеет одну и ту же «колоколо-

Частота

1250

152 165 178 191 РОСТ, CM

Рис. 5.1. Полигон частот для роста 8585 взрослых людей, родившихся в Англии в XIX в.¹

' Гласе Дж., Стенли Дж. Статистические методы в педагогике и психологии. М., 1976. С. 98.

49

Часть I. Основы измерения и количественного описания данных

образную» форму (см. рис. 5.1). Форма таких распределений может быть описана ма­тематической формулой, которую предложил еще в XVIII веке математик де Муавр.

Де Муавр решал следующую задачу. Предположим, монета в азартной игре подбра­сывается 10 раз, и каждый раз она может с равным успехом выпасть «орлом» или «реш­кой». Какова вероятность того, что в результате этой игры выпадет 0 «орлов», или 1 «орел», ..., 10 «орлов»? Сложные вычисления дают математически точное решение такой задачи (рис. 5.2). А если игра состоит из 100 подбрасываний монеты, или 1000? Де Муавру удалось доказать, что уравнение кривой, соединяющей вершины отрезков на рис. 5.2, для данного случая или для любой другой подобной задачи имеет следую­щую формулу:

(5.1)

где/(х,) — высота подъема кривой, е — основание натурального логарифма (пример­но 2,718), л — число «пи» (примерно 3,14), Ми а — среднее и стандартное отклонения для переменной х„ которые определяют положение кривой на числовой оси и задают ее размах. Эта формула и соответствующая ей кривая (см. рис. 5.2) впоследствии по­лучили название закона нормального распределения.

Итак, исход азартной игры, и продолжительность жизни, и рост человека — все это случайные события, частота (или вероятность) встречаемости которых подчинена закону нормального распределения. А. Кетле объяснял это существованием «идеала» человеческой природы, которому соответствуют средние значения различных пока-

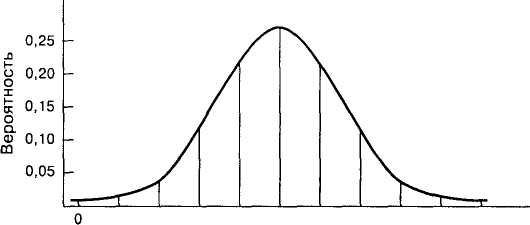
8

10

1 2 3 4 5 6:

Число «орлов»

Рис. 5.2. График распределения вероятностей выпадения «орлов» в игре с 10 подбрасываниями монеты и кривая нормального распределения

50