Лекция №4

4.1.1 Изотермический процесс

Изотермический процесс – это процесс подвода или отвода теплоты от рабочего тела при постоянной температуре рабочего тела ( ).

Запишем уравнение состояния идеального газа для начального и конечного состояний газа:

(4.1)

(4.2)

Выразим из первого и второго уравнений:

(4.3)

(4.4)

Левые части этих уравнений равны. Соответственно равны и правые части этих уравнений:

(4.5)

Поскольку мы рассматриваем изотермический процесс, при котором , то зависимость между начальными и конечными параметрами в изотермическом процессе следующая:

(4.6)

Формулу (3.33) можно переписать в другом виде:

(4.7)

Запишем первый закон термодинамики:

(4.8)

Поскольку в изотермическом процессе , то изменение внутренней энергии идеального газа равно и вся теплота, подводимая к газу, расходуется на совершение работы газом:

(4.9)

Механическая работа определяется по формуле (35):

(4.10)

Интегрирование этой формулы при условии дает следующее выражение для работы:

(4.11)

Однако не совсем ясно, какое давление следует подставлять в формулу (4.11) - или .

Поэтому, вычислить механическую работу идеального газа по формуле (4.11) не представляется возможным.

Для определения механической работы в формуле (4.10) необходимо заменить Р на его выражение из уравнения состояния идеального газа:

(4.12)

Подставим формулу (61) в выражение (36):

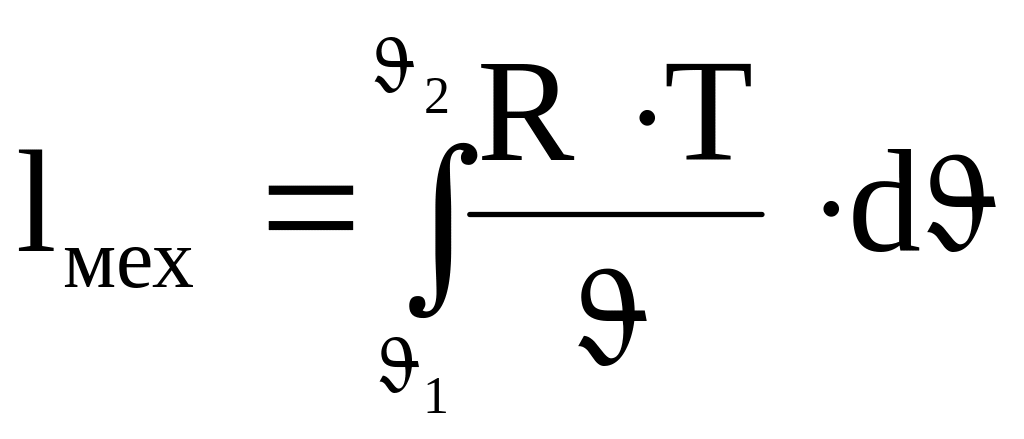(4.13)

В выражении (4.13) газовая постоянная R и температура Т- константы (поскольку рассматривается изотермический процесс) и их можно вынести за интеграл:

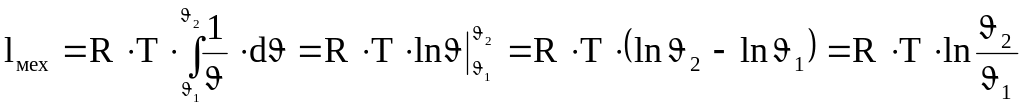(4.14)

Поскольку для изотермического процесса справедливо соотношение:

(4.15)

то:

(4.16)

В формулах (63) и (65) в соответствии с уравнением состояния идеального газа выражение можно заменить на либо .

4.1.2 Адиабатный процесс

Адиабатный процесс – это процесс, происходящий без теплообмена рабочего тела с окружающей средой или, другими словами, без подвода или отвода теплоты от рабочего тела ( ).

Зависимости между начальными и конечными параметрами в адиабатном процессе следующие:

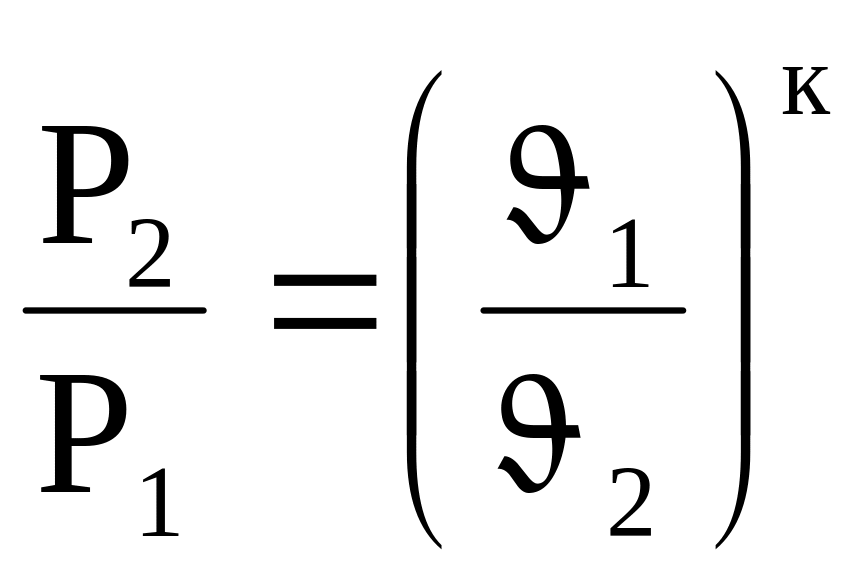(4.17)

(4.18)

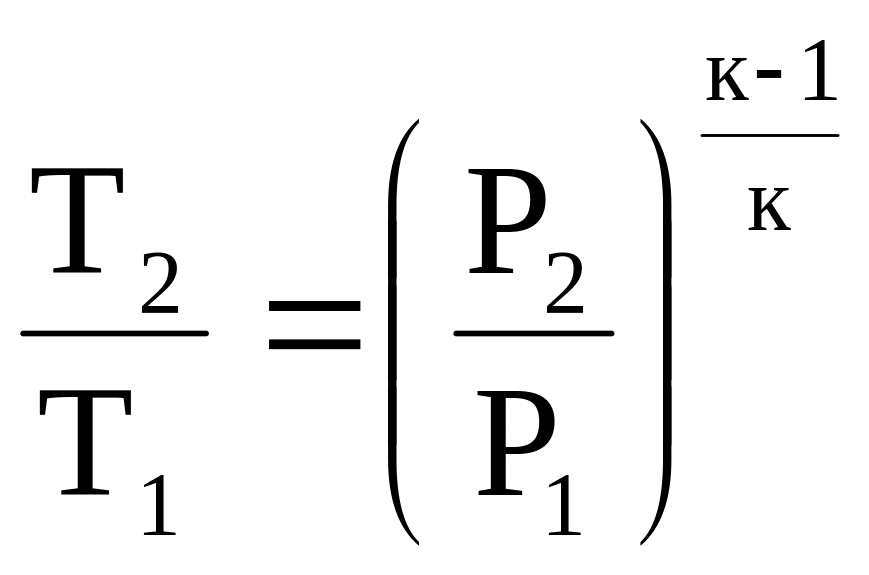(4.19)

где к- показатель адиабаты:

(4.20)

Одноатомный газ
Двухатомный газ
Трехатомный газ

Запишем первый закон термодинамики:

(4.21)

Поскольку в адиабатном процессе , то первый закон термодинамики для адиабатного процесса имеет следующий вид:

(4.22)

или:

(4.23)

Механическую работу газа в адиабатном процессе можно определить по формулам:

(4.24)

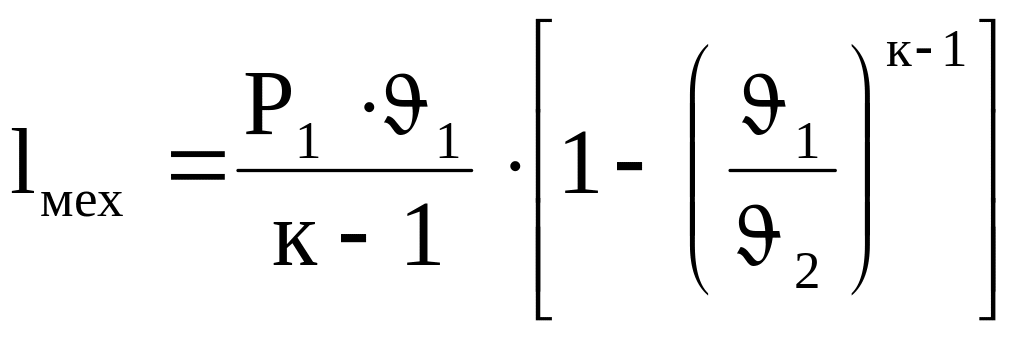(4.25)

(4.26)

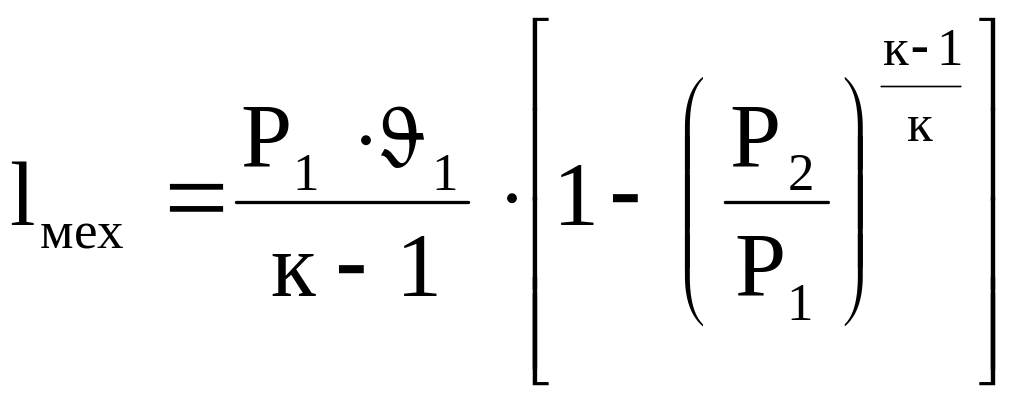(4.27)

Таким образом, в адиабатном процессе рабочее тело может совершать работу только за счет уменьшения своей внутренней энергии.

4.2 Второй закон термодинамики

Первый закон термодинамики утверждает, что теплота может превращаться в работу.

Первый закон термодинамики “позволяет” превратить всю подведенную к рабочему телу теплоту в работу , что может быть осуществлено в изотермическом процессе:

(4.28)

Второй закон накладывает более жесткие ограничения и утверждает, что работа должна быть меньше подведенной теплоты:

(4.29)

на величину отведенной теплоты :

(4.30)

Таким образом, для полного анализа термодинамических процессов необходимо иметь кроме первого закона термодинамики еще дополнительную закономерность. Этим законом является второй закон термодинамики.

Одна из формулировок второго закона термодинамики:

Д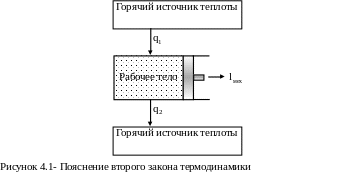 ля существования теплового двигателя необходимы 2 источника - горячий источник (теплота от сгорания топлива) и холодный источник (окружающая среда).

На первый взгляд кажется, что между первым и вторым законами термодинамики существует противоречие: первый закон термодинамики позволяет превратить всю подведенную к газу теплоту в работу, второй закон термодинамики- не позволяет этого сделать.

Однако, в действительности, противоречия между первым и вторым законами термодинамики не существует, потому что первый закон термодинамики говорит о термодинамическом процессе, а второй закон термодинамики говорит о термодинамическом цикле.

Для работы теплового двигателя необходимо, чтобы рабочее тело (газ), к которому подводится теплота и с помощью которого совершается работа, совершало замкнутый процесс и возвращалось в свое п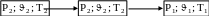 ервоначальное состояние, т.е.:

Этот замкнутый процесс называется круговым процессом или циклом.

Работа, как цикла, так и процесса, изображается в координатах.

1-а-2- кривая процесса расширения рабочего тела; 2-б-1- кривая процесса сжатия рабочего тела.

Площадь под кривой 1-а-2 равна работе расширения газа, площадь под кривой 2-б-1 равна работе сжатия газа, а площадь, ограниченная замкнутой кривой (кривой цикла) 1-а-2-б-1 представляет собой работу, совершаемую газом в циклическом процессе. Отсюда следует, что для того, чтобы работа, совершаемая газом в циклическом процессе, была положительной и вообще существовала, необходимо, чтобы кривая процесса сжатия газа 2-б-1 в координатах была расположена ниже кривой расширения 1-а-2.

4.3 Энтропия идеального газа

Энтропия представляет собой функцию состояния термодинамической системы, т.е. энтропия зависит от параметров состояния системы, а именно от абсолютного давления ( ), плотности ( ) и абсолютной температуры ( ).

Основным уравнением для определения изменения энтропии в обратимом процессе является выражение:

(4.31)

Обратимыми называются процессы, в результате протекания которых в прямом и обратном направлениях в прямом и обратном направлениях термодинамическая система возвращается в исходное состояние, не вызывая при этом никаких изменений в окружающей среде (например, изменения температуры окружающей среды).

Привести пример с перемещением металлического шарика между двумя плоскостями.

Формула (4.31) показывает, что и имеют одинаковые знаки, следовательно, по характеру изменения энтропии в обратимом процессе можно судить о том, в каком направлении протекает процесс. При подводе теплоты к рабочему телу его энтропия возрастает ( ), а при отводе теплоты энтропия рабочего тела убывает.

Поскольку в теплотехнических расчетах в основном приходится рассчитывать не саму величину энтропии термодинамической системы (рабочего тела), а ее изменение, то отсчет значений энтропии можно вести от любого состояния рабочего тела. Для газов принято считать значение энтропии равным нулю при нормальных условиях.

Определение энтропии при постоянной теплоемкости (т.е. в расчетах полагается, что теплоемкость не зависит от температуры) осуществляется по следующим формулам:

(4.32)

(4.33)

(4.34)

Изменение энтропии при переходе газа из состояния 1 в состояние 2, т.е. при осуществлении термодинамического процесса определяется по следующим формулам:

(4.35)

(4.36)

(4.37)