Диал или триз? о законах развития технических систем (для продвинутых читателей)
Сколько законов технических систем вообще может быть? Сколько их должно быть вообще? Для геометрии, например, оказалось достаточно всего пяти постулатов. Для механики – трёх законов Ньютона оказалось недостаточно. А сколько нужно? Пока полной ясности нет.
Как правило, законы вначале появляются на основе экспериментальных данных. Это так называемые эмпирические законы. При построении теории предмета (критерий «аксиоматичности») она включает эмпирические законы в качестве частных случаев.
Яркий пример тому – эмпирические законы Фарадея, «растворившиеся» в дальнейшем в электродинамической теории Максвелла. Знаменитый продолжатель его дела американский физик Ричард Фейнман выразился так: «В истории человечества (если посмотреть на нее, скажем, через десять тысяч лет) самым значительным событием XIX столетия, несомненно, будет открытие Максвеллом законов электродинамики. На фоне этого важного научного открытия гражданская война в Америке в том же десятилетии будет выглядеть провинциальным происшествием».
А наш выдающийся соотечественник Генрих Саулович Альтшуллер чисто эмпирически, на основе анализа патентного фонда, нашёл следующие законы развития технических систем (Альтшуллер, 1979):
✓ полноты частей системы;
✓ «энергетической проводимости» системы;
✓ согласования ритмики системы;
✓ повышения идеальности системы;
✓ неравномерности развития частей системы;
✓ перехода в надсистему;
✓ перехода с макроуровня на микроуровень;
✓ повышения степени вепольности.
Однако поиск законов может осуществляться не только эмпирически (хотя это очень распространённый способ), но и из базовых принципов (универсалий) с проверкой в эксперименте (на практике). В нашем случае – имея мощный инструментарий Диала (сплав теории симметрии и диалектики) – более естествен второй подход. Универсалии, на которых построен язык Диал, имеют более общий характер, нежели законы и закономерности более или менее узких предметных областей, в том числе ТРИЗ. Например, операторы рождения и уничтожения применяются во множестве приложений: в квантовой механике они обеспечивают механизм вторичного квантования, в арифметике (Д. Гильберт) отвечают за порождение чисел. Оператор жизни встречается в экономике в виде жизненного цикла товара, в квантовой механике он порождает число частиц в микросистеме.
В ТРИЗ оператор жизни соответствует «4 возрастам» системы. И вот здесь необходимо остановиться подробнее. В экономике жизненный цикл товара обычно изображают в виде функции, похожей на нормальное распределение (колоколообразной).
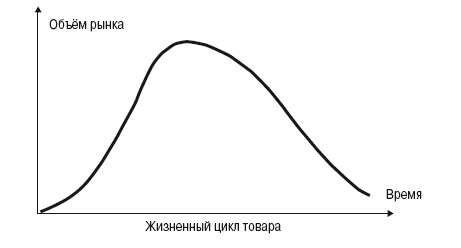
Однако такой вид жизненный цикл товара имеет только приблизительно в 20 % случаев. В остальных же случаях кривая может получить неожиданное продолжение – типа изображённого на рисунке. В результате усовершенствования товара рынок может получить второе дыхание.
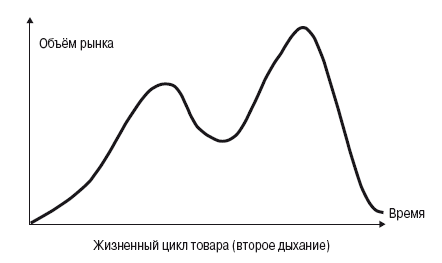
Возможны и другие варианты. Для многих товаров жизненный цикл до сих пор не окончился – например, лопата, ложка, кружка, бритва и т. д. И возможно, окончится только вместе с жизненным циклом человечества. Некоторые товары в процессе эволюции видоизменяются столь сильно, что трудно однозначно сказать: это прежний товар или уже другой. Поскольку технические системы – одновременно и товары, то сказанное справедливо и относительно них. Легко увидеть, что простые системы развиваются медленно – и чем сложнее система, тем быстрее она развивается. Например, та же вилка или ложка остаются неизменными веками. А компьютер развивается с такой скоростью, что потребитель с трудом успевает за его эволюцией.
Справедливости ради надо заметить, что появились современные ложки, интегрирующие в себя градусники, изготовленные из новых материалов (пластмасс, керамик, стекла), но это всё – просто влияние массовых технологий, заставляющих технико‑экономическую среду изменяться.
Можно и нужно сформулировать новый закон : « Чем сложнее техническая (или технико‑экономическая) система, тем быстрее она развивается». Объяснение этого закона довольно просто. Чем сложнее система, тем больше положительных обратных связей её охватывает. А именно положительные обратные связи в технико‑экономических системах ответственны за ускорение научно‑технического прогресса.
После приведенных рассуждений закон неравномерности развития частей системы становится банальностью. Ведь ясно, что некоторые части системы более важны для потребителя, нежели другие, и поэтому интенсивность попыток их усовершенствования гораздо выше, чем для тех, которые менее важны или более‑менее устраивают потребителя. К тому же часть элементов системы может быть охвачена более сильными обратными связями, что в совокупности и приводит к увеличению скорости изменений. Например, персональный компьютер. Скорость совершенствования его центрального процессора несравнима со скоростью совершенствования корпуса, функциональных кнопок, дизайна, системы охлаждения и т. д., ибо процессор охвачен сильнейшими обратными связями, чьё действие обеспечивает выполнение закона Мура [47] . Суть этих обратных связей (в упрощённом виде) проявляется по цепочке. Улучшение процессора обеспечивает создание более мощного программного обеспечения, позволяющего проектировать всё более мощные процессоры и технологии их производства.
Закон полноты частей системы, открытый Г.С. Альтшуллером и воспринимавшийся как откровение, ныне воспринимается как нечто само собой разумеющееся. Было бы странно представить себе жизнеспособной систему, у которой какая‑либо важная для функционирования часть не работает. А именно так осуществляется у Альтшуллера сравнение самолёта Можайского (использовавшего паровой двигатель) и самолёта братьев Райт (разработавших первый бензиновый авиационный мотор) [48] .
Закон «энергетической проводимости» системы, на наш взгляд, является частным случаем закона «полноты частей системы». Трудно представить себе инженера, который, нарушая этот закон, надеется на то, что получит работоспособную техническую систему. И этот факт не зависит от того, знает ли инженер о существовании этого закона или нет, как эффективность мышления не зависит по большому счёту от знания строения мозга.
Считать этот «закон» законом или не считать – вопрос спорный. Например, третий закон Ньютона тоже имеет тривиальный характер, но в системе механики могут встретиться задачи, в которых его применение может быть нетривиальным [49] .
Вернёмся к операторам Диала. Оператор перехода одно‑многое в проекции на техническую систему или технический объект производит закон «перехода моно системы в би– и полисистему», являющийся частным случаем закона «перехода в надсистему». Собственно последовательное применение операторов одно‑много и много‑одно, осуществляющих в Диале порождение количества и его жизненный цикл, в ТРИЗ сопоставимо с переходом моно‑би‑поли‑моно, то есть свертыванием системы.
Закон перехода «макросистемы в микросистему» соответствует изменению масштаба, в процессе которого существенно меняются свойства самой системы. В настоящее время происходит полномасштабный переход технологий в область нано. Как известно, в области наноразмеров свойства наночастиц могут измениться до неузнаваемости, так как на таких масштабах характерный размер объектов сравним с длиной пробега электрона, что и оказывает решающее влияние в наномире.
В Диале имеется мощный оператор меры (прорыва меры), в частных случаях представляемый как оператор изменения масштаба, фазового перехода или состояния. Операторы Диала гораздо богаче по содержанию именно потому, что они строятся из первопринципов. Здесь у нас нет ни малейшего желания умалить заслуги великого учёного Генриха Альтшуллера, получившего выдающиеся для своего времени результаты, когда авторы эти строк ещё «под стол пешком не ходили». Но оператор меры в своих частных проявлениях применим к спектру задач, далеко превосходящему задачи поиска новых технических решений.
Закон повышения «степени вепольности», из которого вырастает важная составная часть ТРИЗ – вепольный анализ, соответствует операторам Диала: вещество‑поле, поле‑вещество и поле‑вещество‑поле, вещество‑поле‑вещество и т. д. Закон «вепольности» обладает большой эвристической силой, для решения изобретательских задач. Операторы Диала, соответствующие ему, не так конкретны. Зато имеют гораздо большую – практически неограниченную – сферу применения. Следует заметить, что использование абстрактных операторов само по себе требует ещё дополнительной работы по конкретизации и адаптации их в предметную область.
Ни для кого не секрет, что в процессе эволюции удельные характеристики технических систем улучшаются: мощность двигателя по отношению к его массе растёт, удельный расход топлива на единицу мощности уменьшается, растёт прочность материалов на единицу массы, увеличивается дальность связи при уменьшении мощности излучателей и т. д. Этот факт отражает важный закон повышения «степени идеальности» системы в ТРИЗ. Превращение этого положения в максиму или принцип: «система стремится к полюсу идеальности» превращает его в мощный эвристический инструмент. Этот мощный принцип ТРИЗ заставляет исследователя правильно сориентировать направление своих поисков и даже подсказывает лучшее решение.
Однако, как замечал сам Альтшуллер, закон повышения степени вепольности входит в некое противоречие с законом «повышения степени идеальности», так как, по словам автора ТРИЗ, введение веполя есть шаг назад (или в сторону) от главного направления, задаваемого полюсом идеальности (Альтшуллер, 2003).
На самом деле в этом нет ничего необыкновенного, так как главный закон любой технической системы или её цель – не попасть на «полюс идеальности», а выжить в условиях жёсткой конкуренции и занять свою экотехнологическую нишу.
Б.И. Кудрин выделяет закон «технобиологического подобия» [50] . Это проявление одного из случаев так называемых ранговых распределений, возникающих в условиях борьбы за ограниченные ресурсы, что наблюдается в дикой природе, в эволюции технических и даже социальных систем (Ёлкин, Журова, 2010). В математической форме ранговое распределение описывается законом Ципфа – Мандельброта и является одним из фундаментальных, универсальных распределений [51] .
Природные объекты подчиняются действию многих законов. Например, по закону всемирного тяготения тело должно было бы падать на землю, если оно не имеет опоры или подвеса, однако это не мешает птицам и самолётам летать, опираясь на воздух, а сильным магнитам висеть в воздухе или вакууме без видимой опоры. Другой пример: гравитационное поле на ядерных масштабах несравнимо мало по сравнению с сильным взаимодействием [52] . Однако именно оно, гравитационное, определяет движение планет, звёзд и галактик. То же происходит и в технических системах. Задача инженера, выявить, какой закон развития в данных условиях может оказать существенное воздействие на техническую систему, и найти именно то техническое решение, которое наилучшим образом соответствует этому закону. Скорее всего, это будет то решение, которое либо не разрушает согласованность технической системы, либо ещё больше повышает её.
Закон «согласования ритмики системы». Замечательная находка Г.С. Альтшуллера, однако совершенно непонятно, почему согласована должна быть только ритмика системы. В любой технической или живой, или вообще какой‑либо системе для жизнеспособности должно быть согласовано как можно больше частей и процессов. Трудно представить себе какой‑либо механизм, у которого не согласованы хотя бы крепёжные элементы (например, диаметры болтов и гаек). В Диале согласование ритмики также имеет важное значение – как в речи и составлении сложных слов, так и в порождении операторов. Почему – становится понятным при работе с контекстом.
Но сначала несколько примеров в тему – на родном языке.