Основные свойства Гауссовых случайных процессов.

1) Гауссовский случайный процесс исчерпывающим образом определяется средним значением и ковариационной функцией

m(t)=<x(t)>;

B(t₁,t₂)=<x(t₁)x(t₂)> - <x(t₁)><x(t₂)>=K[t₁,t₂] - <x(t₁)><x(t₂)>

2) Для гауссова случайного процесса некоррелированность тождественна стат. независимости

В=0K[t₁,t₂]= <x(t₁)><x(t₂)>

;

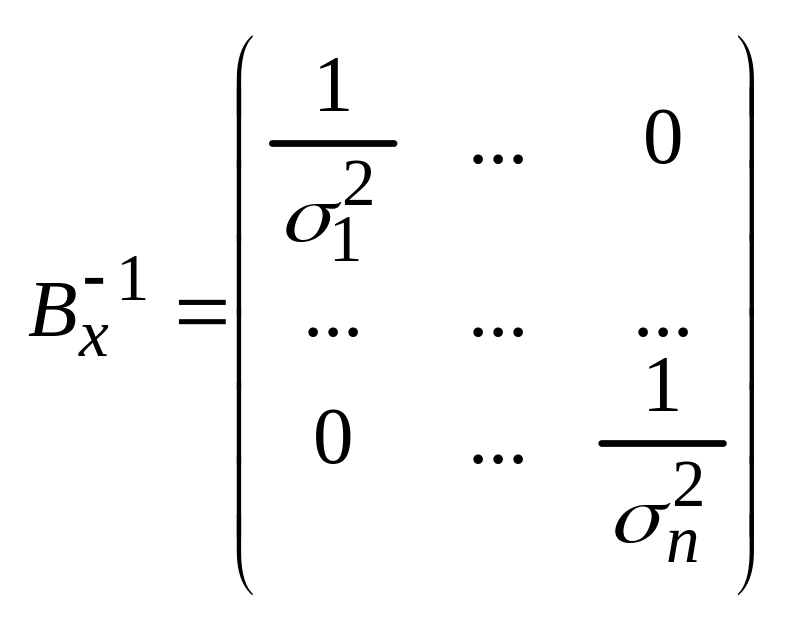
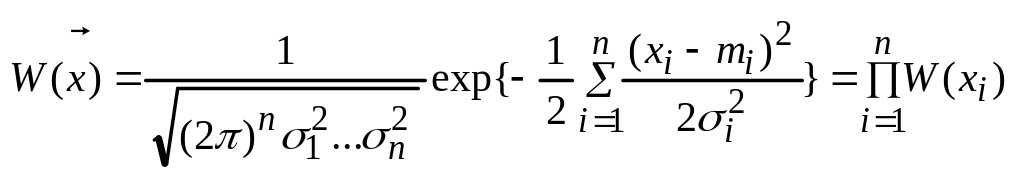
3. В результате любого линейного преобразования гауссовых случайных процессов получаются гауссовы случайные процессы.

4. любая лин. комбинация с.г.п. есть с.г.п.

z(t)=αx(t)+βy(t)

5. любая усл. плотность вер-ти с.г.п. имеет гаусовск. форму

6. с помощью лин. преобразований корр.(завис.) значений с.г.п x(t) можно преобразовать в систему стат. незав.(некорр.) г.с.величин

7. x(t)- с.г.п.

Любые моментные функции гауссовых случайных процессов выражаются через его m(t_k) и B(t_k,t_l)

предположим <x(t)>=m_x(t)=0

<x(t₁),x(t₂)>=α₂(t₁,t₂)=B_x[t₁,t₂]

α₄(t₁,t₂,t₃,t₄)= B_x[t₁,t₂] B_x[t₃,t₄]+ B_x[t₁,t₃] B_x[t₂,t₄]+ B_x[t₁,t₄] B_x[t₂,t₃]

α_2m(t₁,…,t_2m)=(2m-1)!!{ B_x[t₁,t₂] B_x[t₃,t₄]… B_x[t_2m-1,t_2m]}

№13 Стационарные случайные процессы. Понятия стационарности в узком и широком смысле, их взаимоотношение

Опр. 1(стационарность в узком смысле(строгая)):

Случайный процесс x(t) стационарен в узком смысле, если все его n-мерные плотности вероятности инвариантны относительно сдвига во времени, т.е.

W(x₁,t₁;…;x_n,t_n)= W(x₁,t₁+;…;x_n,t_n+)

для стац. процесса

n=1 W(x,t) = W(x,t+) ,   W(x,t) = W(x)

n=2 W(x₁,t₁;x₂,t₂) = W(x₁,t₁- t₁;x₂,t₂- t₁)= W(x₁,0;x₂,t₂- t₁)= W(x₁,x₂,t₂- t₁),

т.е. зависит только от разностей моментов времени.

Основные характеристики:

Среднее значение равно константе

<x(t)>=

Дисперсия равна константе

Корреляционная функция

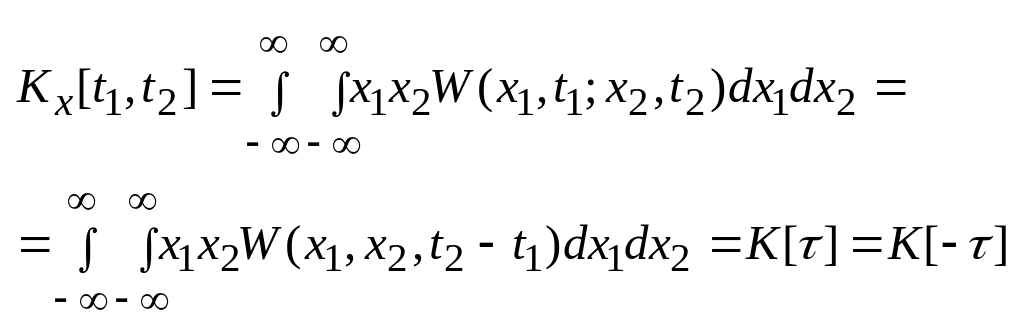
Ковариационная функция

Нормированная ковариационная функция

Опр. 2: (стационарность в широком смысле)

Случайный процесс x(t) стационарен в широком смысле, если

<x(t)>=const, а K_x[t₁,t₂]= K_x[t1-t2]=K_x[]

Для с.г.п. стац. в шир. и в узк. смысле совпадают т.к у них определены только ср. знач. и ковар. ф-ция.

№14. Стационарность квазидетерминированных случайных процессов (рассмотреть на примерах X(t) = A₀cos(₀t + ); X(t) = S(t +₀), где  и ₀ - случайные величины, S(t) - периодическая детерминированная функция).

Квазидетерминированный случайный процесс

x(t)=A₀cos(₀t+) ,  - случайная величина

Среднее значение

<x(t)>= < A₀cos(₀t+)>= A₀<cos(₀t+)>=

=A₀<cos(₀t)cos - sin(₀t)sin>=A₀[cos(₀t)<cos> - sin(₀t)<sin>]

=0

Следовательно, <x(t)>=0, т.е. не зависит от времени

Корреляционная функция

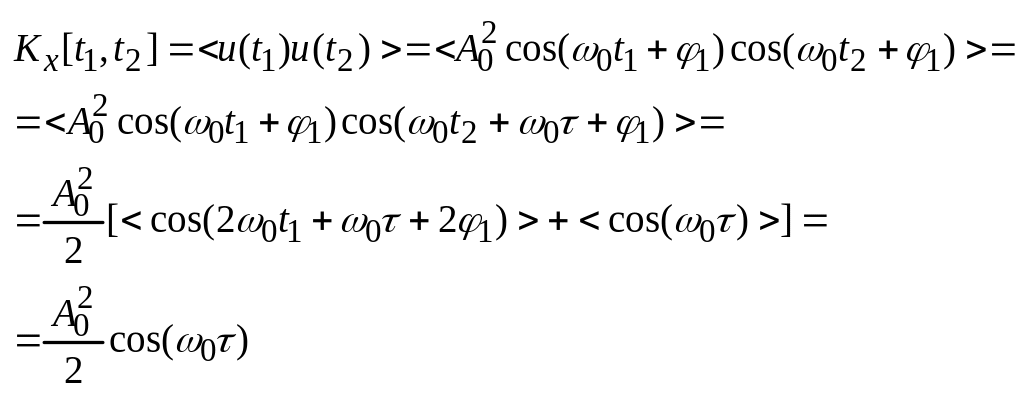
зависит только от t₂-t₁=

_n(…) инвариантны по времени, т.е. можно доказать инвариантность в широком смысле.

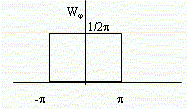
Квазидетерминированный случайный процесс со случайной начальной величиной ₀. x(t)=S(t+₀), S(t)- детерминированная функция с периодом Т

W (₀)=

Среднее значение

<x(t)>=<S(t+₀)>= ,

т.е. не зависит от времени

Корреляционная функция

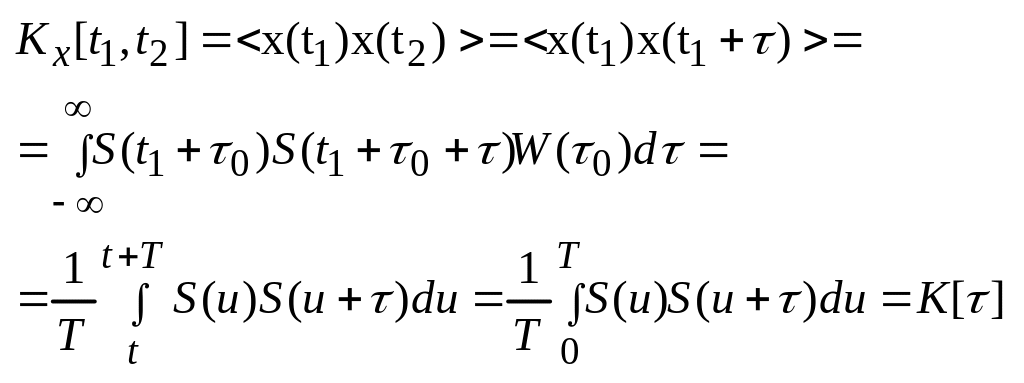
т.е. зависит только от t₂-t₁=

Вывод: Все квазидетерминированные случайные процессы порожденные периодическими функциями с равномерно распределенным по периоду началом, стационарны, по крайней мере, в широком смысле.

№15 Эргодичность случайных процессов. Вывод необходимых и достаточных условий эргодичности по отношению к среднему значению .

Эргодичность по отношению к среднему значению случайного процесса.

x(t) – стационарный случайный процесс.

Вопрос: как найти среднее значение по одной реализации?

- среднее по времени от "к"-й реализации.

, или нет? (<x> - средний по стат. ансамблю.) (*)

Для гарантии сходимости (*) для всех "к" к значению <x>, рассмотрим случайную величину

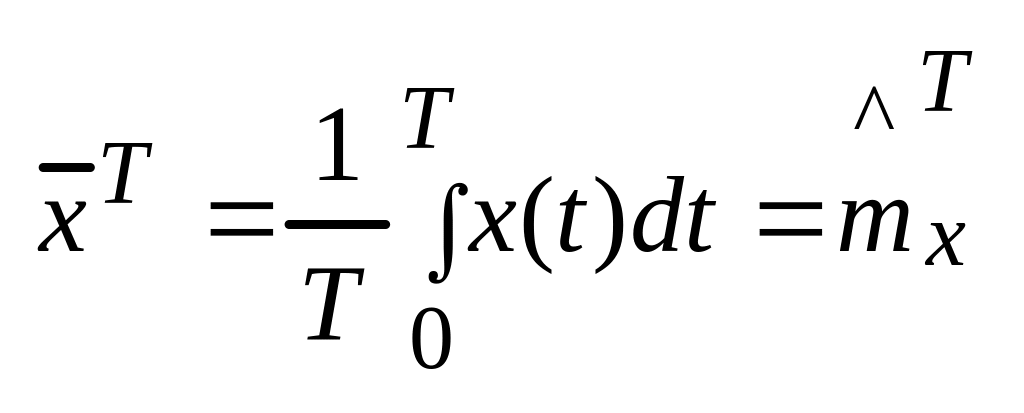(2.6.3)

Определение: Говорят, что случайный процесс x(t) обладает эргодическим свойством относительно среднего значения, если среднее по времени (2.6.3) при T → ∞ сходится к среднему по стат. ансамблю.

- оценка среднего статистического значения.

(2.6.4)

Сам процесс называется эргодическим.

Вопрос: Каким дополнительным условиям должен удовлетворять стационарный случайный процесс, чтобы быть эргодическим по отношению к среднему в среднеквадратическом смысле.

;

={ }=

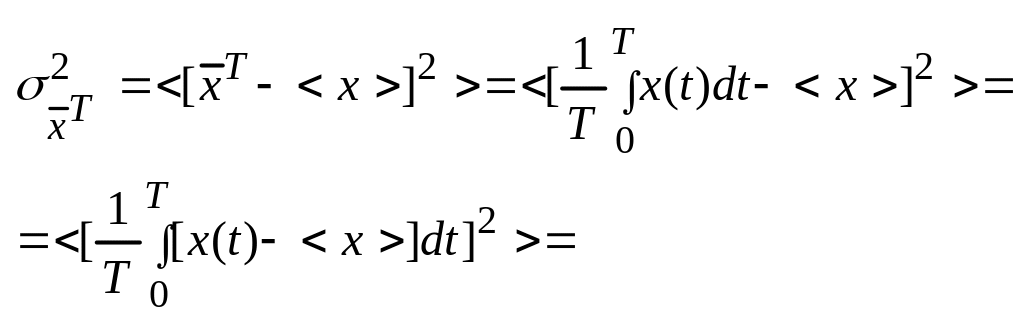
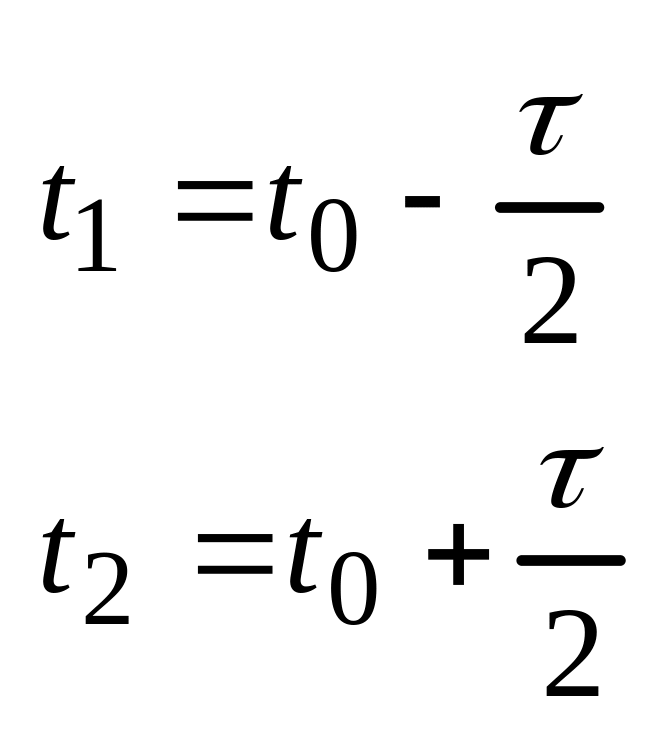={ } {якобиан обратных преобразований равен 1}=

(2.6.5) (дисперсиная оценка функции ),

- симметричная функция.

Из (2.6.5) следует: