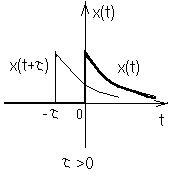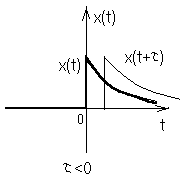29. Преобразование спектральной плотности энергии и функции корреляции случайных сигналов I-ой группы при прохождении их через линейные сист.

Усредним формулу (3.3.10)

Будем считать, что линейная система детерминирована, тогда

(3.3.16)

Возьмем обратное преобразование Фурье от формулы (3.3.16), при этом по теореме о свертке обратное Фурье-преобразование от произведения превратиться в свертку:

(3.3.17)

где - функция корреляции первого рода импульсной характеристики (3.3.18)

Значит, квадрат модуля переходной характеристики – это прямое преобразование Фурье от функции корреляции первого рода импульсной характеристики:

(3.3.18’)

Зарисуем схему взаимосвязи импульсной характеристики, переходной характеристики, функции корреляции первого рода импульсной характеристики и

квадрата модуля переходной характеристики (Рис.2).

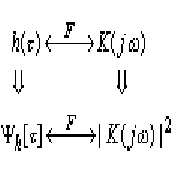
Обратные переходы между импульсной характеристикой и функцией корреляции, между переходной характеристикой и ее квадратом невозможны, т.к. происходит потеря информации о фазе.

Пример 1. Дан детерминированный импульс . Найдем функцию корреляции первого рода

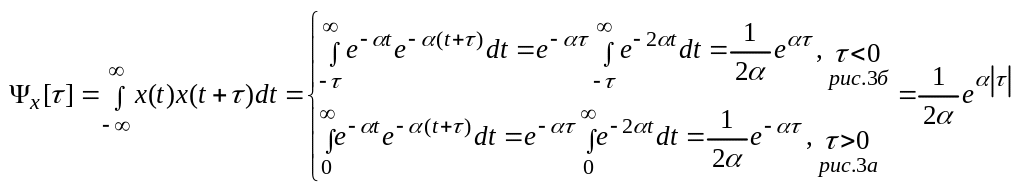
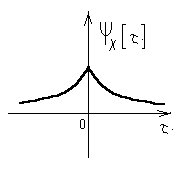
Полученная функция корреляции первого рода изображена на рис.4.

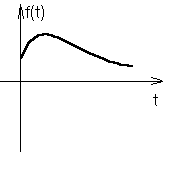
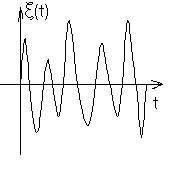
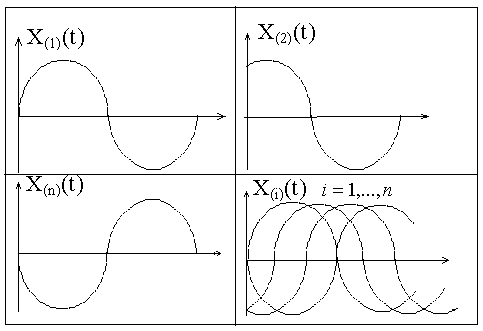
Пример 2. Рассмотрим сигнал x(t)=f(t)ξ(t) , изображенный на Рис.5в, где f(t) – некоторый детерминированный импульс первой группы (Рис.5а), а ξ(t) – стационарный случайный процесс (Рис.5б). Пусть задано K_ξ[τ], а <ξ(t)>=0. Найдем функцию корреляции первого рода сигнала x(t).

Возьмем прямое преобразование Фурье от этой функции:

- получили формулу обратной свертки. Здесь - спектральная плотность мощности сигнала ξ(t), а - средняя спектральная плотность сигнала f(t)

№5 Квазигармонический процесс X(t) = A₀cos(₀t + ) со случайной начальной фазой, равномерно распределенной в интервале [-,]. Его одномерная плотность вероятности.

,  - случайная фаза.

З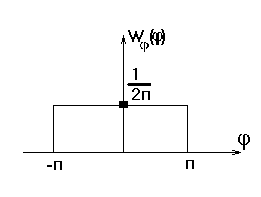 афиксируем , тогда процесс будет детерминированным.

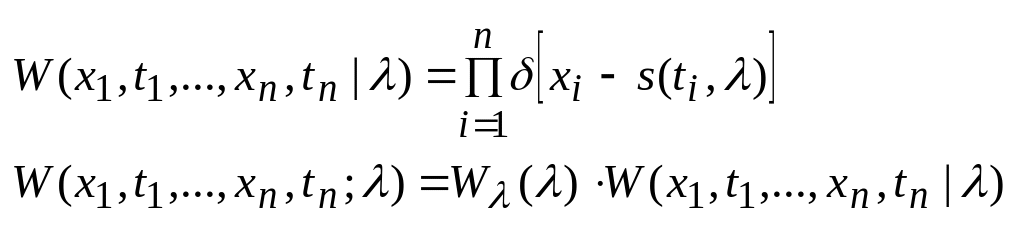
Свойство согласованности:

№9 Ковариационная функция случайного процесса. Дисперсия. Понятия некоррелированности и статистической независимости двух значений случайного процесса. Коэффициент корреляции.

B[t₁,t₂] = χ₂(t₁,t₂) – ковариационная ф-ция

B[t₁,t₂] = <x(t₁),x(t₂)> – <x(t₁)><x(t₂)> = K_x[t₁,t₂] – <x(t₁)><x(t₂)> =

= [x(t₁) – <x(t₁)>]•[x(t₂) – <x(t₂)>]

Опр. Если значение ковариационной ф-ции равно 0 для t₁, t₂, то говорят, что значения сл.пр. в эти моменты времени не коррелируют.

B[t,t] = <x(t)²)> – <x(t₁)>² = σ_x²(t) – дисперсия (она может меняться во времени)

Из стат. независимости → некоррелируемость (обр. неверно)

Стат. независимость:

Нормированная корреляционная ф-ция (коэф. корреляции)

№10. Гаусовские случайные процессы, их n-мерная характеристическая функция и плотность вероятности. Информация, необходимая для полного описания гауссовского случайного процесса.

– Гаусовским сл. пр. называется сл. пр. у которого n-мерная характеристическая ф-ция (для любого n и t) будет иметь вид

– Гаусовским сл. пр. называется сл. пр. у которого все кумулянтные ф-ции, начиная с 3-его порядка равны 0.

;

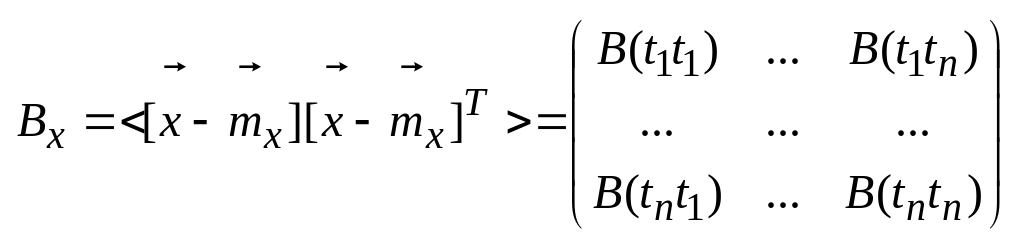
Плотность вероятности выглядит следующим образом:

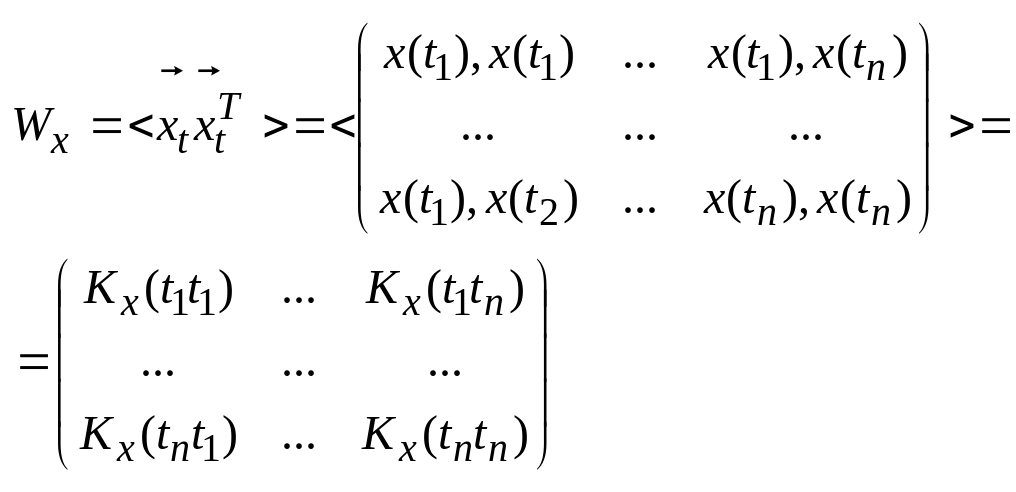
Если n=1 , то

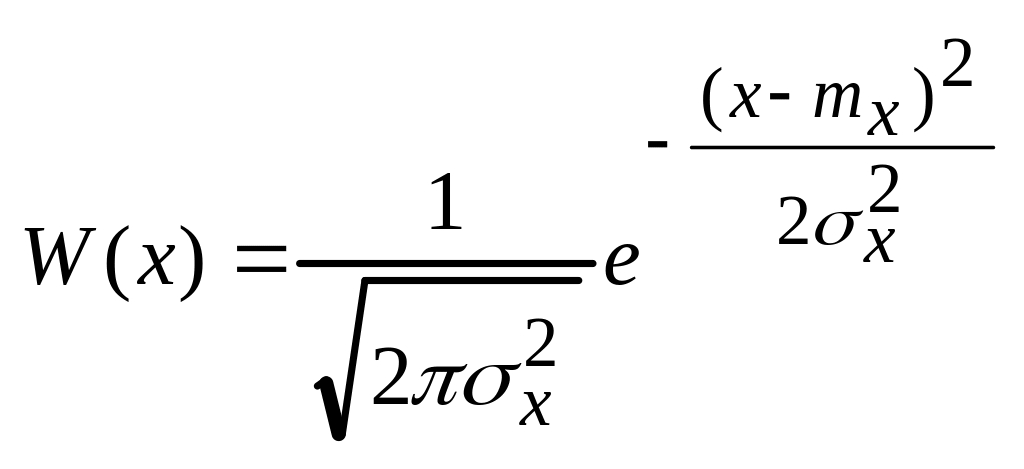
№11 Ковариационная матрица n отсчетов случайного процесса и ее основные свойства.

1. Симметричность B_x^T=B_x следует из симметричности ковариационных ф-ций B(t_n,t_s)= B(t_s,t_n)

2. Свойств полож. опред.

(корр. матрица тоже обладает этим свойством )

Доказательство:

Свойства симметр. матриц:

1. собственные числа вещественные

2. собственные векторы, соотв. разл. собств. значениям, ортогональны

3. Вещественная симметричная матрица А может быть приведена к диагональной форме с помощью ортогонального преобразования Q

|Q|=|Q^T|=1

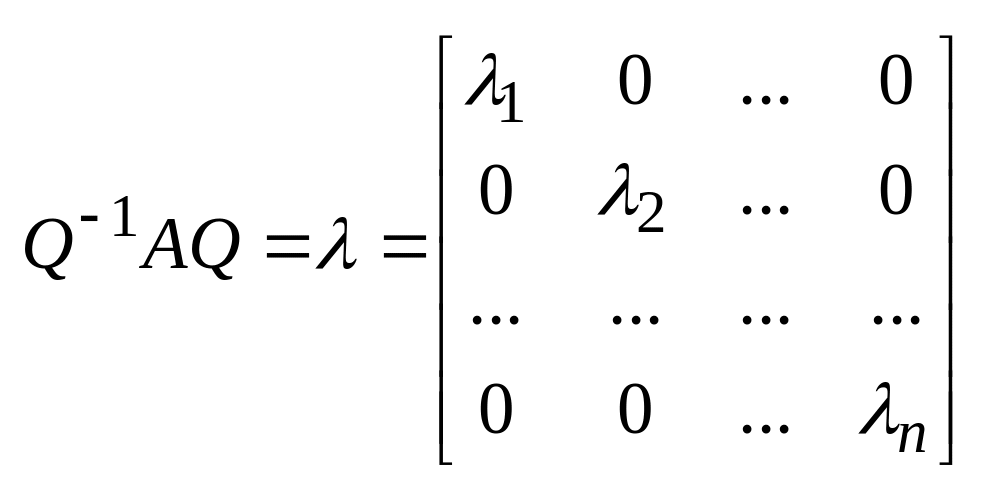
4. необх. и дост. условием полож. определенности веществ. симметр. матрицы А явл. положительность собств. значений.

5. для вещественной полож. матрицы можно ввести

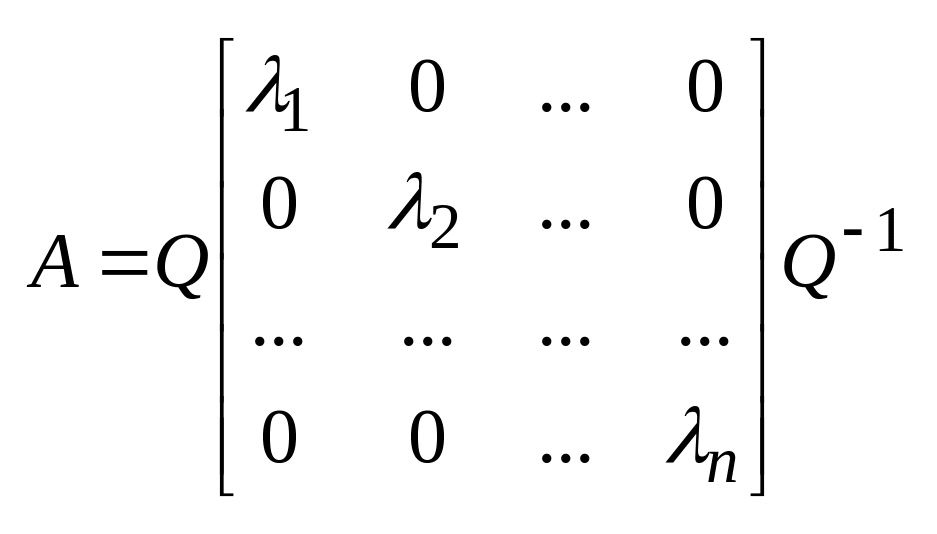
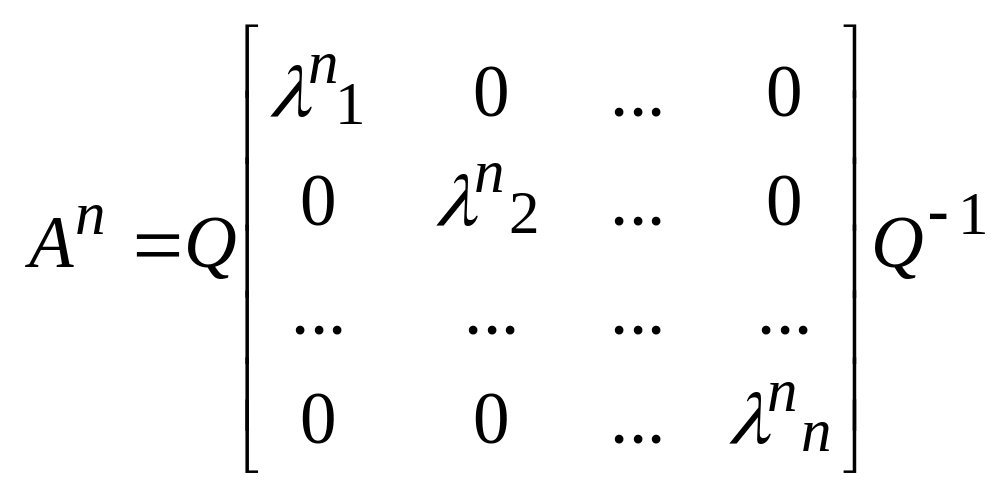
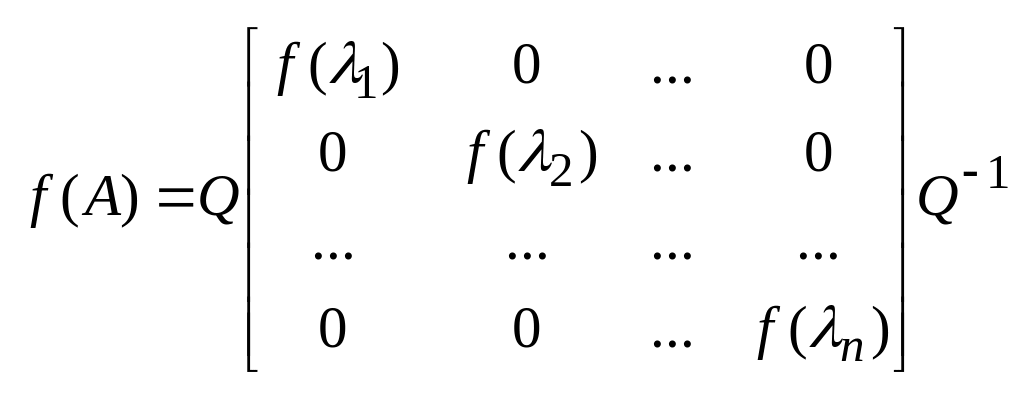
положительно определенная симметр. матрица имеет квадратный корень

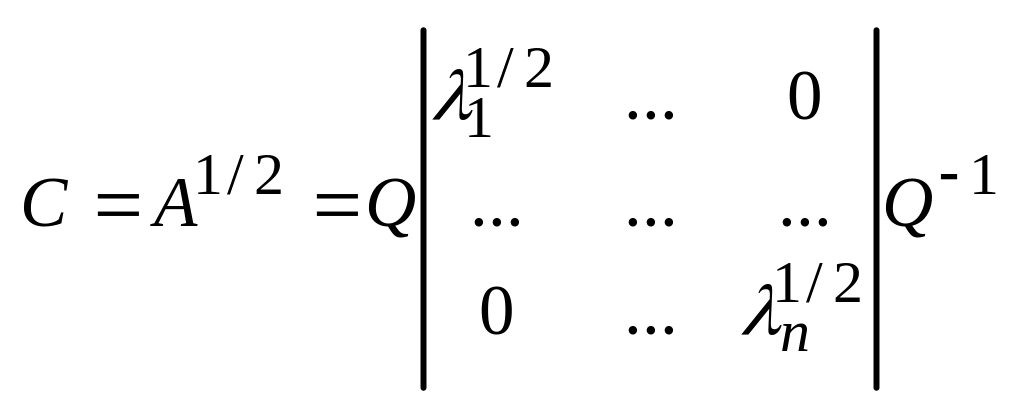
С²=А

№12 Основные свойства гауссовских случайных процессов. Выражение n-мерных моментных функций гауссовского случайного процесса с нулевым средним значением через ковариационную функцию.