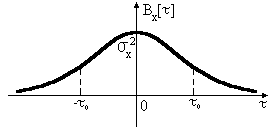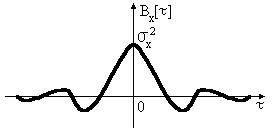2) Положительная определенность:

Для любого момента времени t₁,t₂,...,t_n и любых чисел U_1,U₂ ,...,U_n

справедливо неравенство:

берем X(t) и домножаем на :

можно получить обобщение; U –может быть комплексное значение, тогда

еще случай: X(t)-комплексный случайный процесс и U – комплексный

тогда

Рассмотрим как скалярную случайную величину:

причем считаем U(t) – детерминированной

Все приведенные свойства справедливы и для ковариационной функции, в частности

Ограниченнность по модулю:

(3.1.2’)

(3.1.2’’)

справедливо следующее неравенство:

Знак равенства выполняется во всех формулах 2 имеет место тогда и только тогда, когда между значениями случайных процессов x(t₁),y(t₂) имеет место «жесткая» (детерминированная) линейная зависимость.

y(t₂)=a(t₁,t₂)x(t₁)+b(t₁,t₂)

Д-во:

пусть имеет место линейная детерминированная связь, воспользуемся

_y(t₂)=|a|_x(t₁),

тогда

Обратное утверждение: если

то существует линейная детерминированная связь.

Рассмотрим нормированный центрированный процесс ( Y – такой же )

тогда

22. Свойства корреляционной функции стационарного случайного процесса.

Симметричность

для автокорреляционной функции

для совместной корреляционной функции

2)Ограниченность

3)Положительная определенность

4)А также для большинства случайных процессов с конечной линейной статистической памятью выполняется

Свойства с 1 по 4 будем называть К-свойствами (свойства корреляционной функции для стационарных случайных процессов)

7. Моментные функции случайного процесса. Среднее значение и корреляционная функция. Связь моментных функций с характеристической функцией.

Случайный процесс можно описывать с помощью n-мерной плотности вероятности или n-мерной характеристической функции, но это описание не всегда удобно. Введем моментные функции случайного процесса:

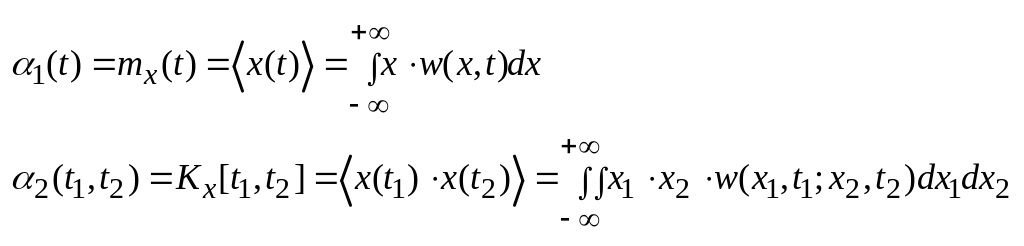
(2.4.2)

Здесь ₁(t) – моментная функция первого порядка, совпадающая со средним значением m_x(t) случайного процесса; ₂ - моментная функция второго порядка, совпадающая с корреляционной функцией K_x[t₁,t₂] случайного процесса; _s - моментная функция порядка s.

Некоторые моменты времени могут совпадать, тогда моментную функцию записывают в виде

и называют n-мерная моментная функция порядка s.

 _i – количество моментов времени, равных t_i

s=₁+...+_n – порядок моментной функции (s  n)

n – мерность моментной функции

Видно, что для нахождения n-мерной моментной функции порядка s нужно знать n-мерную плотность вероятности случайного процесса. В частном случае, при n=1, моментная функция порядка s выглядит так:

Найдем связь моментных функций и характеристической функции случайного процесса. Для этого разложим характеристическую функцию (u₁,t₁;...;u_n,t_n) в ряд Маклорена по аргументам u_i в окрестности u₁ = 0,..., u_n = 0 :

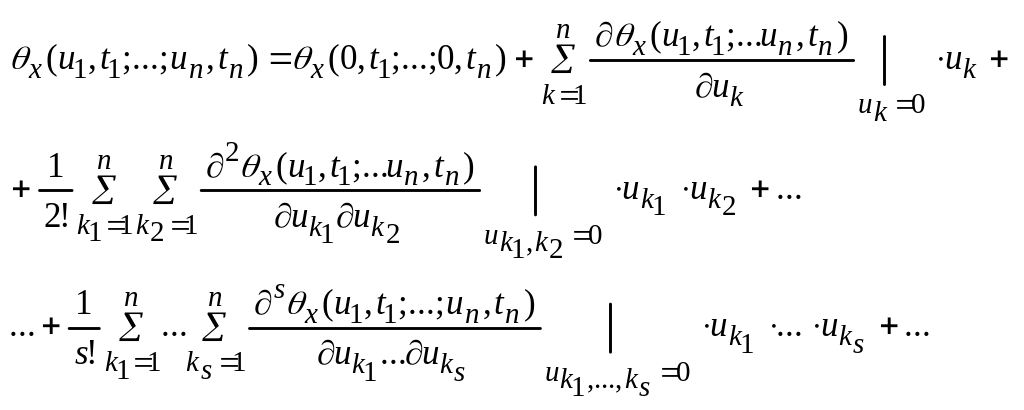(2.4.3)

Рассмотрим частные производные. С учетом условия нормировки характеристической функции получим:

(2.4.4)

С учетом (2.4.4) формула (2.4.3) примет вид:

(2.4.5)

Формула (2.4.5) дает связь моментных функций случайного процесса с его характеристической функцией. Таким образом, задание характеристической функции случайного процесса эквивалентно заданию всех его моментных функций.

Итак, случайный процесс можно описывать n-мерной плотностью вероятности, n-мерной характеристической функцией или n-мерными моментными функциями порядка s. И любой из этих способов полностью характеризует случайный процесс.

Далее рассмотрим еще один способ описания случайных процессов.

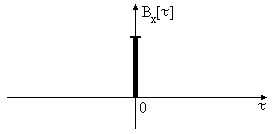
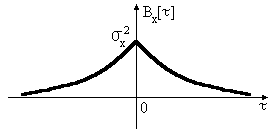
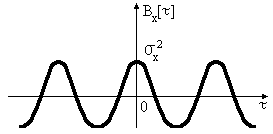
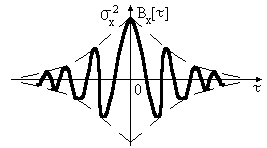
23. Типичные примеры корреляционных функций стационарных случайных процессов. Понятие времени корреляции.

Bx[]=Dx() - удовлетворяет всем K-свойствам Для данного примера дисперсия:	Bx[]=
Bx[]=	Bx[]= - удовлетворяет всем К-свойствам
Bx[]=	Bx[]= , при условии:

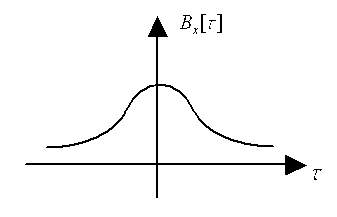
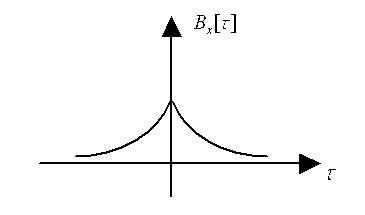
Рассмотрим стационарный случайный процесс:

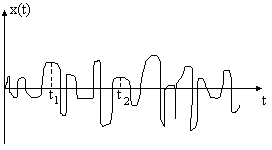
₀ – время, при котором можно пренебречь корреляцией, т.е. время корреляции (будем обозначать его как _корр).

B_x[]/_x²=R_x[]

Время корреляции вычисляется по формуле:

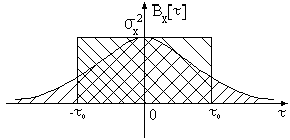Построим на нашем графике прямоугольник (рис. 9).

Тогда площадь прямоугольника будет равна площади под кривой.

Если процесс с заполнением, то интеграл берут по огибающей, т.е.

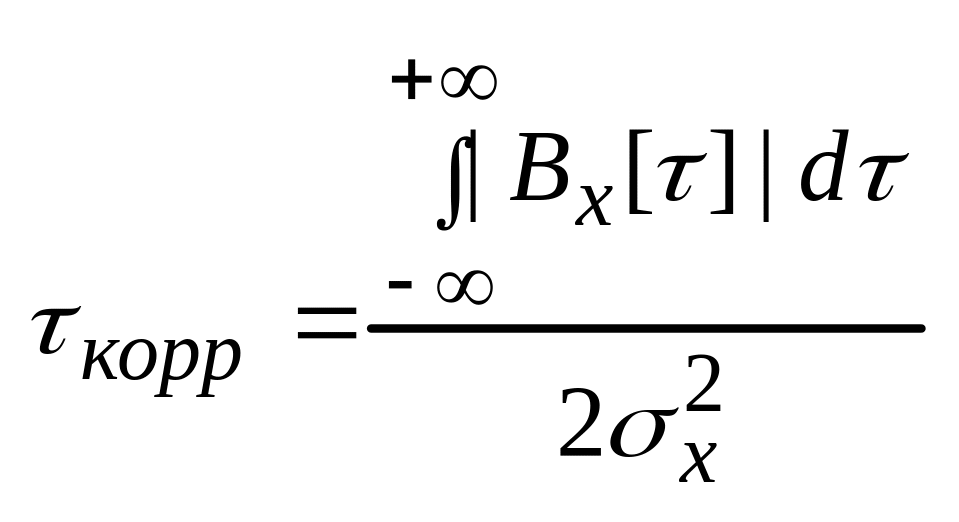
26. Среднее значение и корреляционная функция интегрального преобразования случайного процесса.

,

где -случайный процесс, -детерменированная функция(ядро).

В каком смысле мы понимаем определенный интеграл в среднеквадратичном смысле - пишем сумму Римана , предельный переход в среднеквадратичном смысле.

Найдем среднее значение,

,

, (1)

и кореляционную функцию

= ,

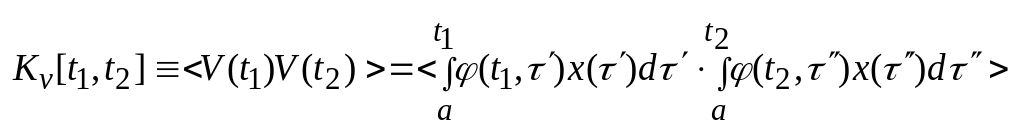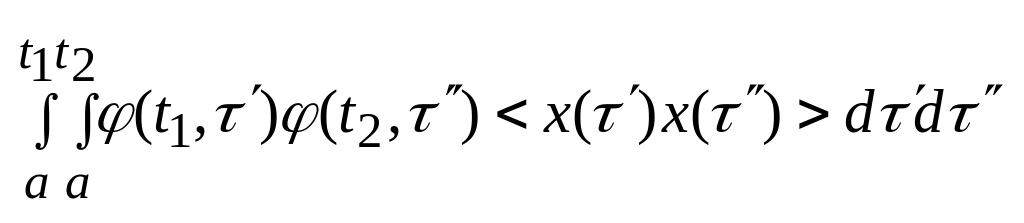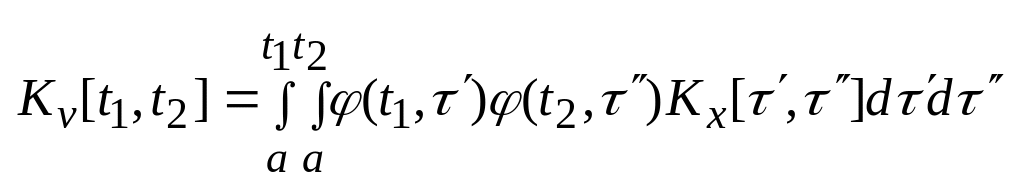, (2)

Имели ли право это делать : Можно строго доказать, что интеграл (1) существует в среднеквадратичном смысле , если существует двойной интеграл (2).

24. Дифференцирование случайного процесса. Корреляционная функция и среднее значение производной от нестационарного случайного процесса.

Пусть у нас имеется случайный процесс x(t) со средним значением m_x(t)=<x(t)> и функцией корреляции K_x[t₁,t₂]=<x(t₁),x(t₂)>. Нам надо найти среднее значение m_z(t) и корреляционную функцию K_z[t₁,t₂] процесса

z(t)=(x(t))’=

m_z(t)=<z(t)>=< >= =

K_z[t₁,t₂]=<z(t₁),z(t₂)>=< , >= = , т.е

K_z[t₁,t₂]=

Рассмотрим случай n-й производной:

=< >= =

=< , >= =

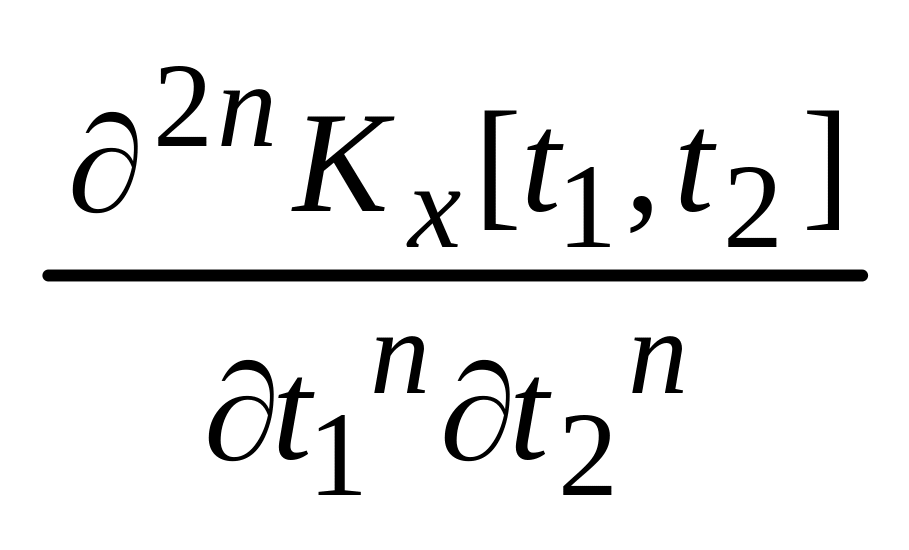
В частном случае:

и .

В общем случае:

28. Спектральная плотность энергии случайных сигналов I-ой группы, функция корреляции I-го рода, ее свойства.

По определению средняя полная энергия сигнала:

(3.3.11)

А средняя спектральная плотность энергии:

(3.3.11’)

Усредняя формулы (3.3.1), (3.3.4), (3.3.5) по статистическому ансамблю, получим

(3.3.12)

Усредняя (3.3.6) по статистическому ансамблю, получим

(3.3.13)

где (3.3.14)

Ψ_x[τ] - функция корреляции первого рода. Она связана со средней спектральной плотностью энергии обратным преобразованием Фурье, т.е.

(3.3.15)

Функция корреляции первого рода обладает всеми К- свойствами корреляционной функции стационарного случайного процесса:

Свойство симметричности:

Ограниченность по модулю:

Свойство положительной определенности: для всех значений ω выполняется .

, т.к. импульсы ограниченны во времени

Спектральная плотность энергии Э_x(ω) обладает свойствами:

для всех значений ω.

Спектральная плотность энергии – четная функция (симметричная), т.е.

, т.к.

Смысл введения функции корреляции первого рода Ψ_x[τ] – найти способ вычисления спектральной плотности энергии Э_x(ω)

25. Производная от стационарного случайного процесса, ее среднее значение и корреляционная функция

x(t) –стационарный, <x(t)>=m_x=<x>.

K_x[t₁,t₂]=K_x[t₂-t₁]=K_x[];

, т.е.

, т.е.

Корреляция и :

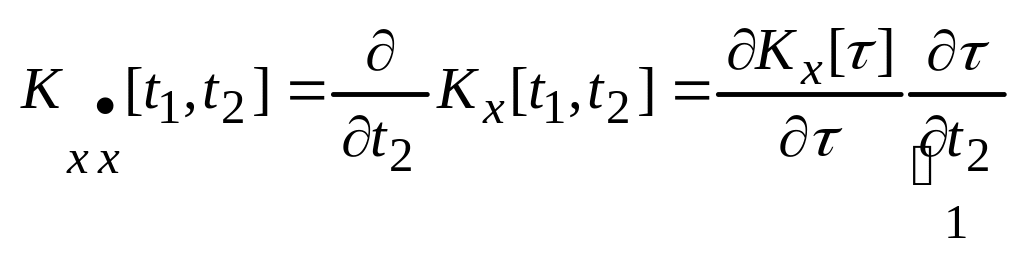
Обобщение на случай производной более высокого порядка:

Пример 1. Стационарный случайный процесс , причем:

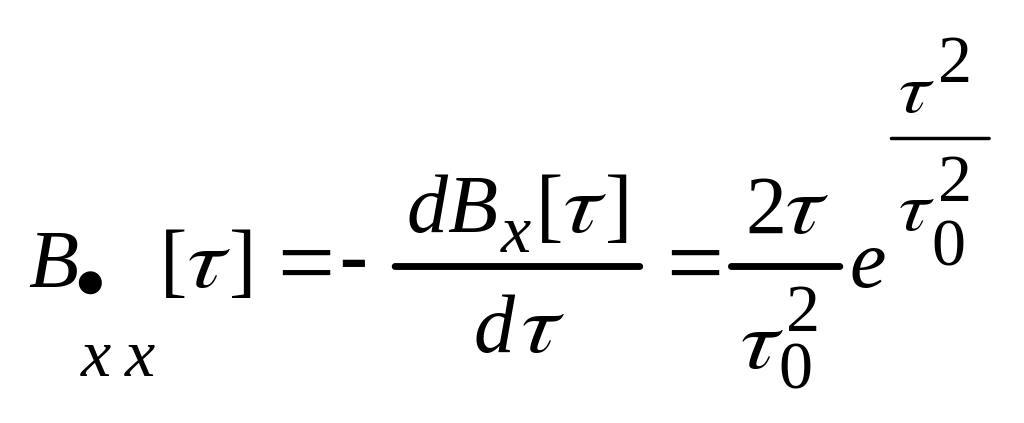
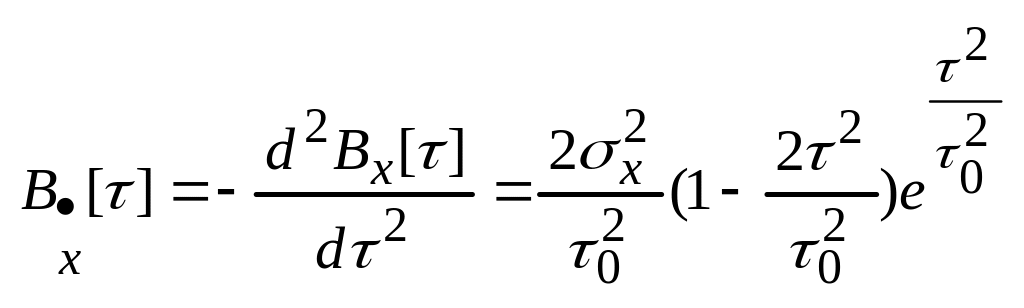
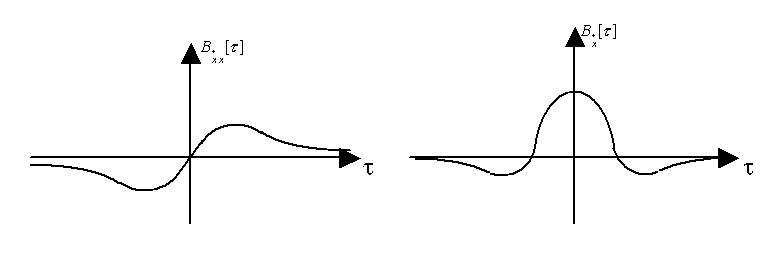
Максимум соответствует нулю .

Вывод: для любого стационарного процесса, его значение и значение его производной в совпадающие моменты времени не коррелированны.

Пример 2. - случайный процесс, причем:

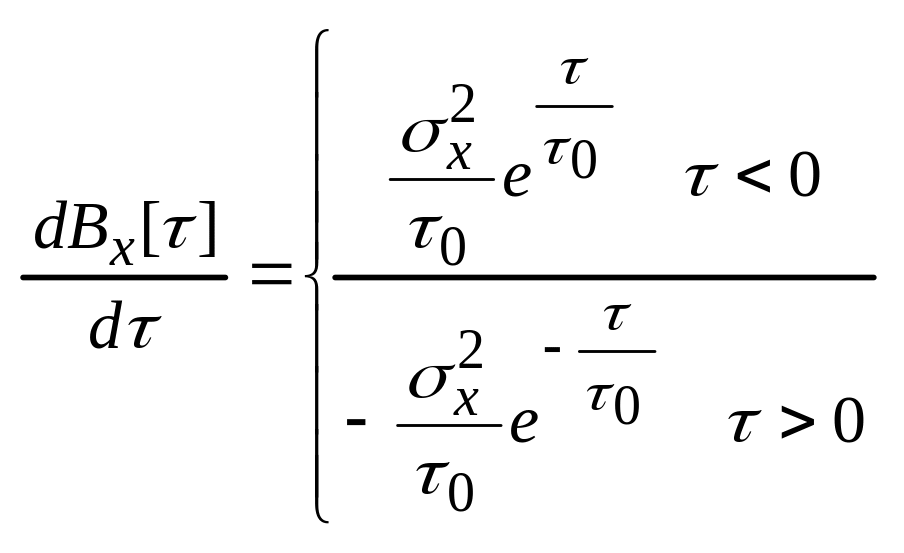
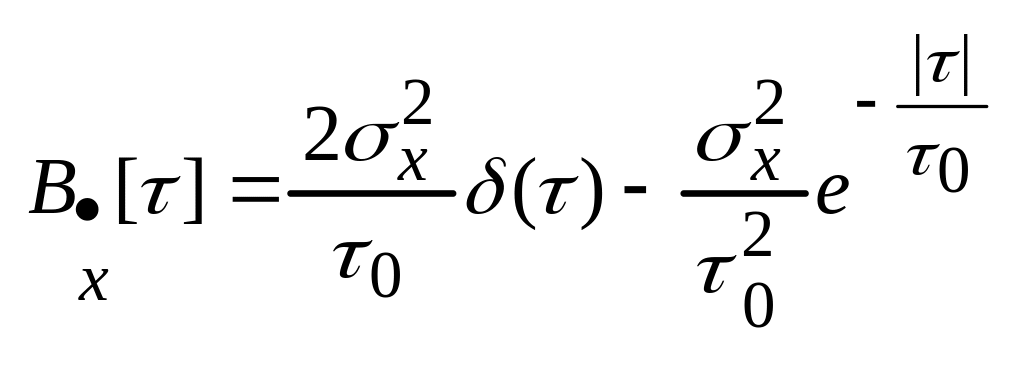
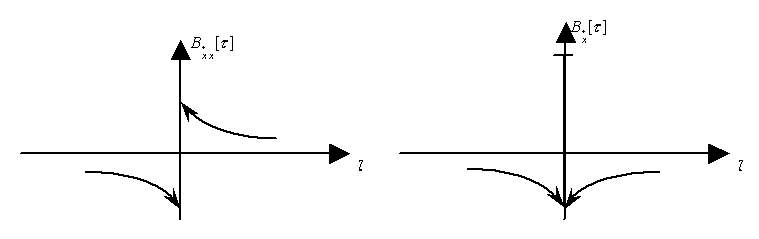
Такой процесс не дифференцируем в среднеквадратическом смысле, т.к. вторая производная

не ограничена

27. Сигналы I-ой группы. Спектральная плотность энергии детерминированного сигнала I-ой группы. Преобразование спектральной плотности энергии детерминированных сигналов I-ой группы при прохождении через линейные системы.

Будем говорить, что принадлежит к сигналам первой группы, если его полная энергия является ограниченной величиной:

(1)

- случайная величина, характеризующая распределение энергии по реализациям случайного процесса.

К сигналам первой группы относятся детерминированные сигналы конечной длительности; бесконечные, но достаточно быстро убывающие; все случайные импульсы. Относится ли стационарный сигнал к сигналам первой группы? У стационарного случайного процесса:

Следовательно интеграл (1) неограничен, т.е. стационарный случайный процесс не является сигналом первой группы.

Спектральная плотность энергии детерминированных сигналов первой группы.

- детерминированный процесс и

Запишем интеграл Фурье:

- спектральные составляющие сигнала.

Выражение энергии сигнала через спектральные компоненты:

Т.к. - действительный процесс

Спектральная плотность энергии не содержит информации о фазовом соотношении между спектральными компонентами.

Спектральная плотность энергии при прохождении через линейную систему.

При прохождении случайного процесса x(t)-сигнала первой группы через линейную систему (см рис.1) процесс на выходе рассматриваемой линейной системы можно записать при помощи интеграла Дюамеля:

(3.3.7)

где h(τ) – импульсная характеристика.

Свойства импульсной характеристики:

Если на вход поступает δ-импульс x(t)=δ(t), то y(t)=h(τ) – отклик системы.

Свойство физической реализуемости: при τ<0 h(τ)=0.

Свойство устойчивости:

Формула (3.3.7) не учитывает начальных условий и описывает отклик системы без учета собственных решений.

(3.3.7)=

Кроме импульсной характеристики для описания линейных систем используется переходный коэффициент передачи K(jω)

Переходный коэффициент передачи K(jω) связан с импульсной характеристикой Фурье-преобразованием , т.е.

(3.3.8)

(3.3.8’)

Как преобразуются спектральные компоненты сигнала?

Если задана функция - свёртка двух функций, то спектральная компонента сигнала преобразуется как

(3.3.9)

Помножаем на комплексно-сопряженную спектральную компоненту сигнала и получаем выражение для средней спектральной плотности энергии сигнала

(3.3.10)