- •4. Детерминированные и квазидетерминированные процессы, их описание в рамках теории случайных процессов, выражения для n-мерных плотностей вероятности.
- •1)Постановка задачи
- •41. Формулировка задачи оптимального обнаружения сигнала на фоне шума при дискретных наблюдениях. Отношение правдоподобия. Понятие достаточной статистики.
- •1)Постановка задачи
- •6.Многомерная характеристическая функция случайного процесса и ее основные свойства.
- •2)Статистическая независимость
- •3)Характеристики совокупности случайных процессов
- •4)Определение некоррелированности случайных процессов
- •20 Понятия стационарности, эргодичности, гауссовости совокупности двух случайных процессов. Разобрать пример двух стационарных, но нестационарно связанных случайных процессов
- •1) Симметричность
- •Ограниченность по модулю:
- •2) Положительная определенность:
- •Ограниченнность по модулю:
- •22. Свойства корреляционной функции стационарного случайного процесса.
- •29. Преобразование спектральной плотности энергии и функции корреляции случайных сигналов I-ой группы при прохождении их через линейные сист.
- •Основные свойства Гауссовых случайных процессов.
- •Опр. 1(стационарность в узком смысле(строгая)):
- •Основные характеристики:
- •Опр. 2: (стационарность в широком смысле)
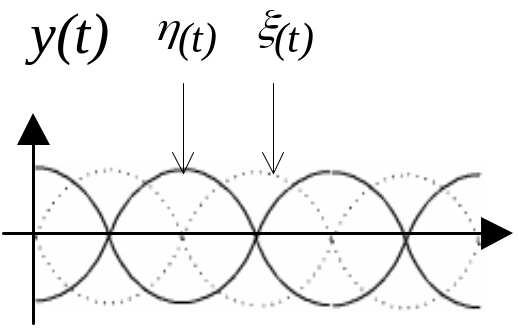
- •Вывод: Все квазидетерминированные случайные процессы порожденные периодическими функциями с равномерно распределенным по периоду началом, стационарны, по крайней мере, в широком смысле.
- •Эргодичность по отношению к среднему значению случайного процесса.
- •Необходимое и достаточное условие эргодичности:
- •Достаточное условие эргодичности Слуцкого:
4)Определение некоррелированности случайных процессов
Два случайных процесса называют взаимно некоррелированными, если их взаимная ковариационная функция тождественно равна нулю для любых моментов времени t1, t2 . Тогда взаимная корреляционная функция «разваливается» на произведение средних, это видно из определения взаимной ковариационной функции. Из статистической независимости случайных процессов следует их некоррелированность, обратное в общем случае неверно, поясним:
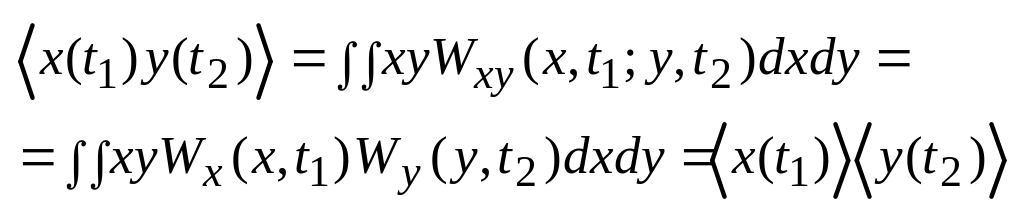 ,
,
однако из утверждения
![]()
не следует утверждение Wxy(x,t1;y, t2)= Wx(x,t1) Wy(y, t2).
20 Понятия стационарности, эргодичности, гауссовости совокупности двух случайных процессов. Разобрать пример двух стационарных, но нестационарно связанных случайных процессов
Свойство стационарности и эргодичности легко распространяется и на совокупности случайных процессов.
Определение: Совокупность случайных процессов {x(t), y(t)} называется стационарной в строгом смысле, если их совместная плотность вероятности любого n+n-го порядка инвариантна к сдвигу во времени.
Определение: Совокупность случайных процессов {x(t), y(t)} называется стационарной в широком смысле, если их средние значения постоянны и все совместные корреляционные и автокорреляционные функции зависят только от разности времён, например:
Автокорреляционная функция в этом случае является чётной относительно , покажем:
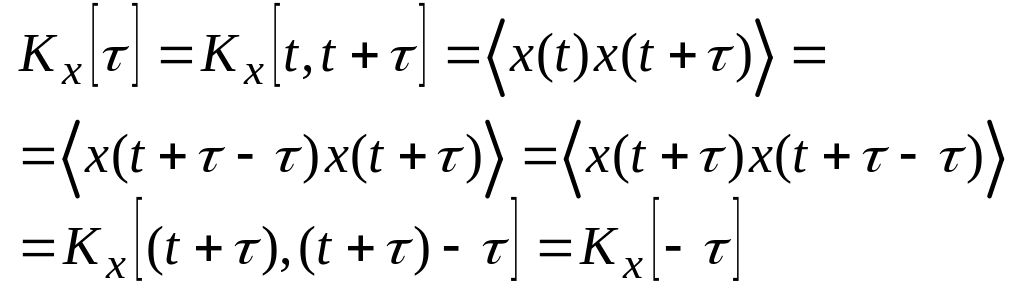 , (2.7.7)
, (2.7.7)
совместная корреляционная функция обладает похожим свойством:
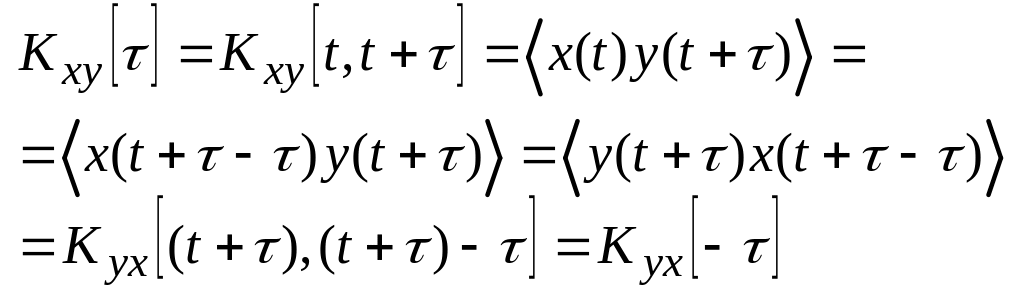 . (2.7.8)
. (2.7.8)
Совокупность {X(t),Y(t)} называется гауссовой, если случайные процессы X(t),Y(t) имеют совместное гауссовское распределение. Вспомним, что вектор есть матрица-столбец :
![]()
![]()
У нас есть вектора наблюдения, составим объедененный вектор:
![]()
О бъеденный вектор имеет гауссовское распределение если вектора X(t),Y(t)– образуют совместное гауссовское распределениеВообще говоря: по отдельности они могут быть гауссовыми, а совокупность не гауссовское распределение:
для n=1, n’=1
задано
W(x,y)
для
![]()
Далее, по умолчанию стационарность будет пониматься, как стационарность в широком смысле.
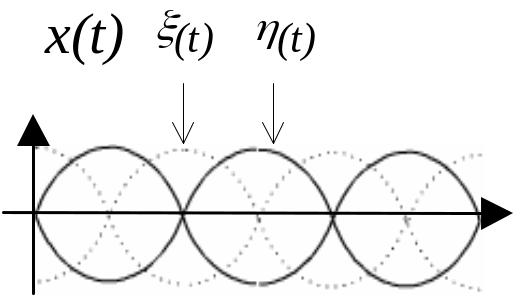
Вообще говоря, если два случайных процесса стационарны по отдельности, то они могут и не образовывать взаимно стационарную совокупность. Рассмотрим частный случай: пусть даны два случайных процесса {x(t), y(t)} такие, что:
![]() ,
,
где (t),(t) – два стационарных случайных процесса с нулевыми средними, причём они некоррелированные между собой и выполняется: K []=K []=K[]. Покажем, что x(t), y(t) – стационарны по отдельности, но образуют взаимно нестационарную совокупность:
![]() ,
,
аналогично:
![]() ,
,
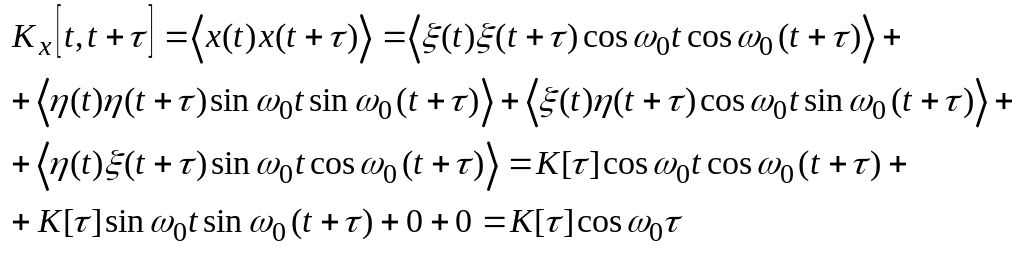 ,
,
для Ky[t, t+] получается такое же выражение, покажем что для взаимной корреляционной функции зависимость от t устранить не удастся:
 ,
,
из чего следует взаимная не стационарность совокупности процессов {x(t), y(t)}.
|
|
|
|
|
|
21.Свойства корреляционной функции произвольного нестационарного случайного процесса.
1) Симметричность
Kx[t1,t2] Kx[t2,t1] (3.1.1)
Kxy[t1,t2] Kyx[t2,t1]
Ограниченность по модулю:
/
Kxy[t1,t2]
/![]() (3.1.2)
(3.1.2)
Д-во:
рассмотрим
![]()
![]()
![]() (3.1.2)
(3.1.2)
при =1, получаем впомагательное неравенство: Kxy[x,y] Kx+Ky