6.Многомерная характеристическая функция случайного процесса и ее основные свойства.

Определение: n-мерной характеристической функцией от n-мерного случайного процесса - n-кратное Фурье преобразование от n-мерной плотности вероятности.

(2.4.1)

n-мерная характеристическая функция дает такое же полное описание случайного процесса как и n-мерная плотность вероятности.

Основные свойства характеристической функции

1. Значение характеристической функции в нуле равно единице

(Условие нормировки плотности вероятности)

2. Условие ограниченности по модулю

3. Свойство симметрии

4. Свойство согласованности

Характеристическая функция для совершенно случайного процесса, также разваливается на произведение n-мерных характеристических функций случайного процесса.

19.Общее описание совокупности двух случайных процессов. Понятие статистической независимости двух случайных процессов. Взаимные корреляционная и ковариа-ционная функции. Понятие некоррелированности двух случайных процессов.

Пусть дана упорядоченная пара случайных процессов {x(t),y(t)}, например x(t) – процесс на входе линейной системы, а y(t) – на выходе линейной системы. В общем случае нас интересует связь этих процессов в любые моменты времени. Полное описание данной совокупности возможно введением совместной плотности вероятности, например если из процесса x(t) берётся n точек, а из процесса y(t) – n точек, то нужно ввести n + n мерную плотности вероятности:

. (2.7.1)

Она обладает всеми свойствами n – мерной плотности вероятности случайного процесса, кроме свойства симметрии, свойство симметрии выполняется не полностью, возможна перестановка аргументов по следующему правилу:

.

2)Статистическая независимость

Два случайных процесса называются статистически независимыми, если их n+ n – мерная плотность вероятности для любых n и n «разваливается» на произведение n – мерной плотности вероятности процесса y(t) и n – мерной процесса x(t):

, (2.7.2)

в противном случае эти процессы статистически зависимы.

3)Характеристики совокупности случайных процессов

Совершенно аналогичным образом можно ввести все те характеристики, которые были введены для одного случайного процесса, например совместная характеристическая функция:

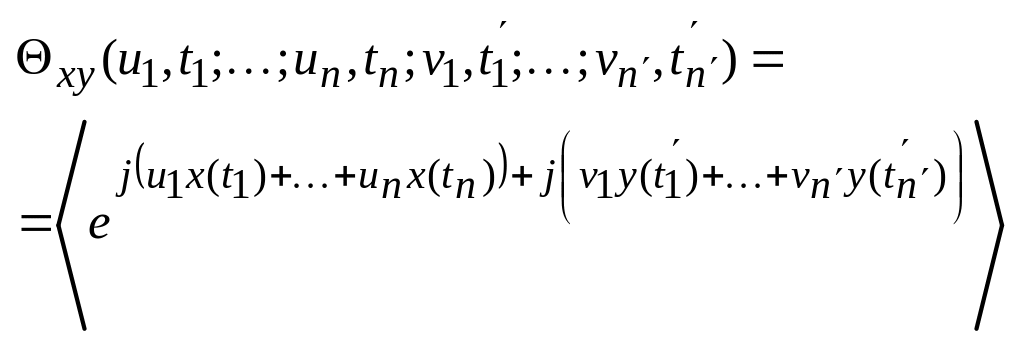, (2.7.3)

здесь усреднение ведётся по всем случайным величинам x и y.

Аналогично введём совместную моментную функцию 2-х случайных процессов s+p-го порядка, как среднее от произведения:

. (2.7.4)

Если процессы статистически независимы, то любая совместная моментная или характеристическая функция «разваливается» на произведение соответствующих функций для каждого процесса по отдельности. (это утверждение 2.7.4)

Наиболее важными статистическими характеристиками случайных процессов являются моментные функции 1-х и 2-х порядков, например пусть x(t), y(t) – два случайных процесса тогда:

,

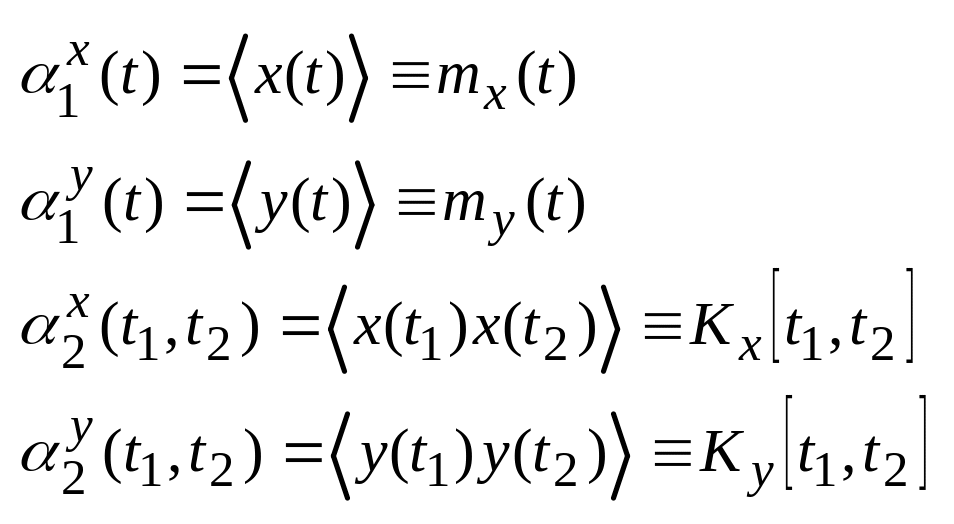где m_x(t), m_y(t) – средние значения, а K_x[t₁, t₂], K_y[t₁, t₂] – корреляционные функции соответствующих случайных процессов. Возникает также смешанный момент 2-го порядка или взаимная корреляционная функция:

. (2.7.5)

Значит можно ввести взаимную ковариационную функцию:

,

и взаимный коэффициент корреляции:

.

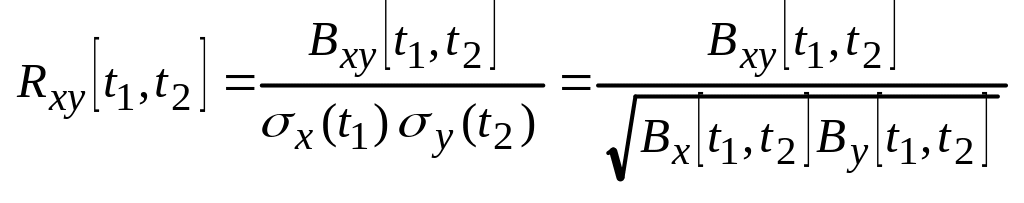Из формулы для взаимной корреляционной функции видно, что она обладает своеобразным свойством симметрии:

, (2.7.6)

из этой формулы видно, что для автокорреляционной функции свойство симметрии будет выполняться в чистом виде:

,

аналогичное утверждению (2.7.6) справедливо также для B_xy[t₁, t₂] и R_xy[t₁, t₂].