1)Постановка задачи

Случайный процесс x(t) называется эргодическим по отношению к какой-то стат. характеристике, если определение этой характеристики путём усреднения по времени по одной реализации совпадает с результатом полученным путём усреднения по стат. ансамблю.

Случайный процесс называется эргодическим в узком смысле, если он эргодический относительно всех своих вероятностных характеристик.

2)Проиллюстрируем вывод условия эргодичности по отношению к корреляционной функции.

Пусть x(t)-стационарный процесс.

-среднее по стат. ансамблю.

Временной аналог:

Что будет, когда ?

Эргодичность процесса по отношению к корр. Функции.

в средне-квадр. смысле.

Введём вспомогательный случайный процесс: y(t)=x(t)x(t+)

Временной аналог представляет из себя среднее по времени от вспомогательного случайного процесса.

в ср.кв. смысле

Условие эргодичности исходного случайного процесса по отношению к корр. функции, это есть условие эргодичности для вспомогательного процесса y(t) по отношению к среднему значению.

(2.6.7)

-условие эргодичности исходного сл.процесса x(t) по отношению к корр. функции.

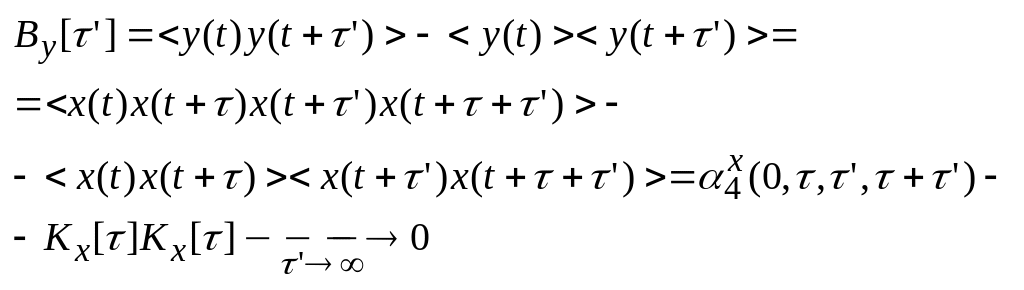
-достаточное условие эргодичности.

Есть зависимость от 4^й моментной функции (0, т.к. инвариантна по отношению к сдвигу вовремени).

Для того чтобы исследовать эргодичность процесса x(t) по отношению к его корр. функции, необходимо знать его 4^ю моментную функцию.

Пусть x(t) -стацонарный гауссовский сл.пр., <x(t)>=0

Пусть

Аналогичным образом можно записать условие эргодичности для любой стат. характеристики.

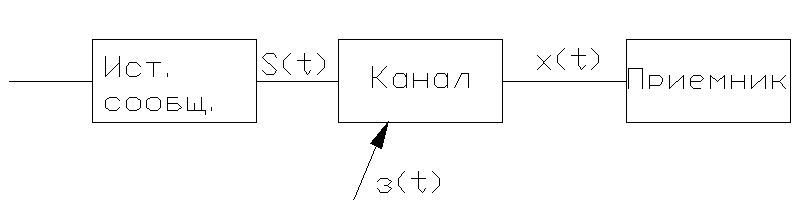
41. Формулировка задачи оптимального обнаружения сигнала на фоне шума при дискретных наблюдениях. Отношение правдоподобия. Понятие достаточной статистики.

1)Постановка задачи

- функции правдоподобия

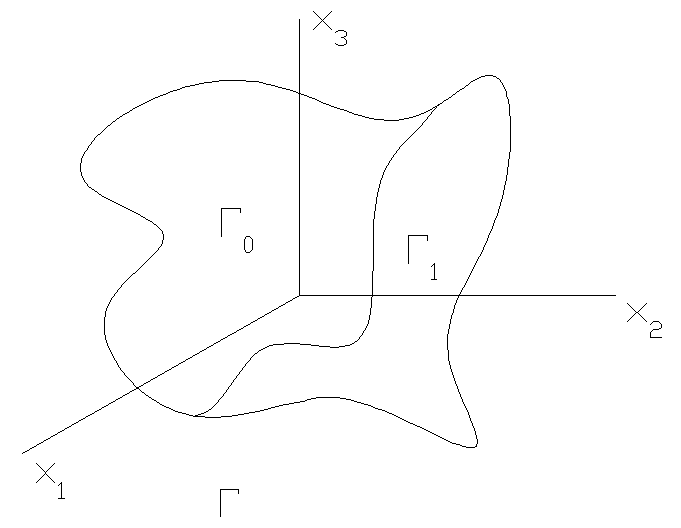
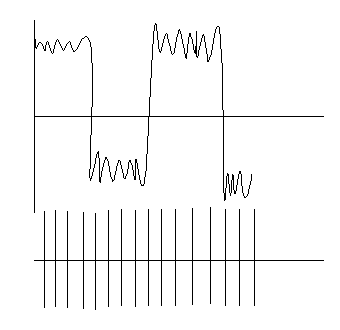
Задача – оптимально разбить область Г на две области - Г₁ и Г₀. (м. разбивать и на 3 области). Г₁ – «да», Г₀ – «нет» (области) => h₁ – «да», h₀ – «нет» (ответы). Ошибки при принятии решения:

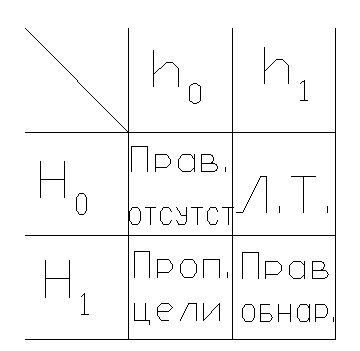(Л.Т. – ложная тревога)

Критерий идеального наблюдателя (Котельников) – P_ошиб = min

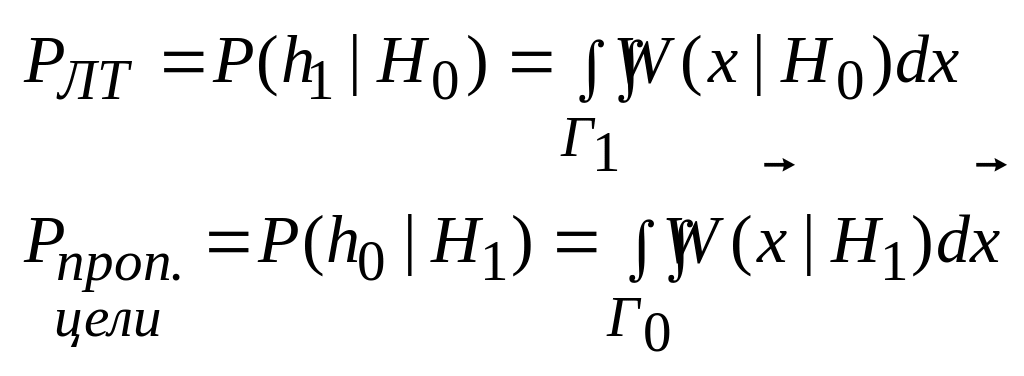
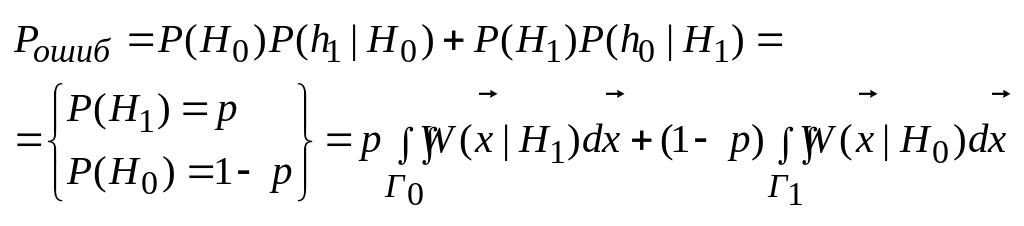
для Г₁ выбираем те x, где подынтегральная функция меньше нуля, -> делаем определённый интеграл отрицательным.

- отношение правдоподобия

сделали разбиение пространства, т.е. если теперь влево поставим конкретный и он принадлежит Г₀ –> то H₀, иначе наоборот. Но для этого мы должны заранее знать . Это есть самое главное условие решение задачи – знание функции правдоподобия: либо знаем, либо нам сказали!

1) z = l(x) – смотрим как на скалярную величину.

Def.: Скалярная величина, в которой находится вся информация для принятия решения называется достаточной статистикой. Z и есть таковая статистика.

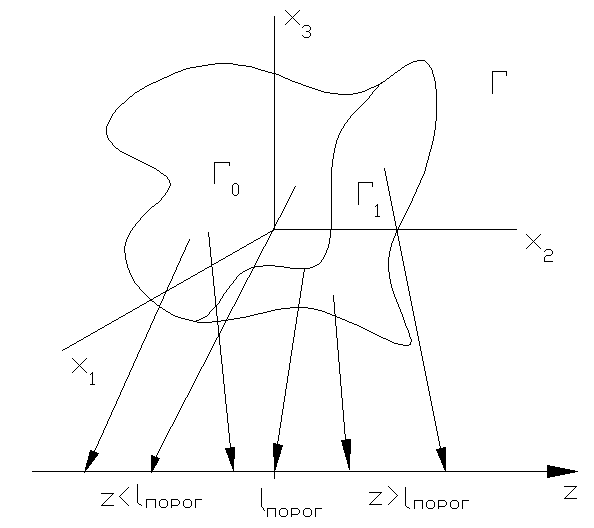
На отношение правдоподобия м. смотреть как на некий алгоритм обработки сигнала.

18. Достаточное условие эргодичности случайного процесса по отношению к одномерной плотности вероятности. Экспериментальное определение одномерной плотности вероятности эргодического случайного процесса.

Пусть x(t) стационарный процесс.

W|(x,t)=W(x)

Что нужно усреднять, когда одна реализация? Как ввести вспомогательный сл. процесс?

Aside: “ формализм ”

Рис. 3

,где x-параметр, x(t)-сл.величина

y(t)=[x-x(t)]

Для детерменированного процесса :

y(t)=[x-x(t)]

W(Х)=<[x-x(t)]>

-ковариационная функция вспомогательного процесса y(t)

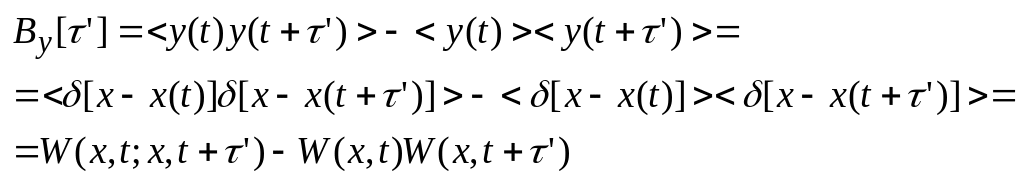
Достаточное условие эргодичности по отношению к плотности вероятности:

Стат. независимые далеко стоящие значения – достаточное условие эргодичности.

Чтобы проверить условие эргодичности сл. пр. по отношению к одномерной плотности вероятности, нужно знать ,как себя ведёт двумерная пл. вероятности.

Экспереметальное определение одномерной пл. вероятности

.

Пусть x(t) эргодичный по отншению к W(Х)

|x(t)[x]

W`-временной аналог.

- реальный сл.пр. в x окрестности.

- относительное время.

W`