1. Определение случайного процесса. Понятие статистического ансамбля. Вероятностное описание случайного процесса с помощью многомерных плотностей вероятности. Основные свойства многомерных плотностей вероятности случайного процесса.

Def. Если для произвольного момента времени t x представляет собой случайную величину, то говорят, что x(t) есть случайный процесс или случайная функция времени.

Def. Случайная функция (процесс) есть множество заданных детерминированных функций (реализаций) случайного процесса, на котором задана вероятностная мера, т.е. вероятность появления каждой из реализаций.

1 случайный генератор – 1 реализация.

Def. Стат. ансамбль – бесконечный набор генераторов (реализаций).

Def. Случайный процесс есть полный набор всех генераторов.

Одномерная плотность вероятности помогает найти вероятность попадание величины в интервал [x,x+dx]: .

- по трм. Чебышева

Для двух моментов времени получаем:

Для n моментов времени:

Будем считать, что случ. Процесс полностью задан, если известно его n-мерное вероятностное распределение для  n и для  моментов времени t₁…t_n.

Свойства:

1.

2.

3. Симметрия: (относительно перестановки любой пары аргументов)

4. Согласованность:

2. Двумерная условная плотность вероятности случайного процесса и ее основные свойства. Зависимость условной плотности вероятности от разности времен для процесса с конечным вероятностным последействием. Многомерные условные плотности вероятности, их свойства и связь с многомерными безусловными плотностями вероятности.

. Отсюда получаем:

Двумерная условная плотность вероятности случайного процесса:

P(AB)=P(A)*P(B|A).

Свойства: (аналогичны безусловной относительно своего истинного аргумента)

1.

2.

Рассмотрим реализацию случайного стационарного процесса. Возьмём два момента времени t₁ и t₂, пусть =t₂-t₁. Тогда:

- события становятся стат. независимы.

Аналогично вводим большую плотность вероятности с большей размерностью:

. Повторяя много раз, получаем формулу:

№31. Спектральная плотность мощности нестационарных процессов II-ой группы. Функция корреляции II-го рода.

x(t) – нестационарный случайный процесс

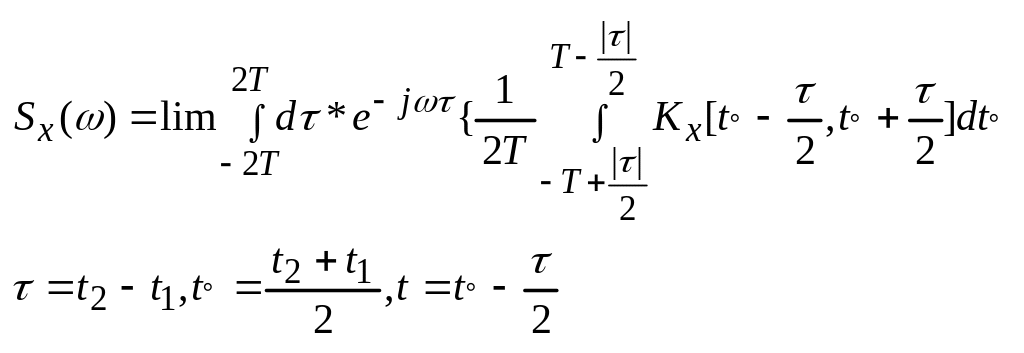
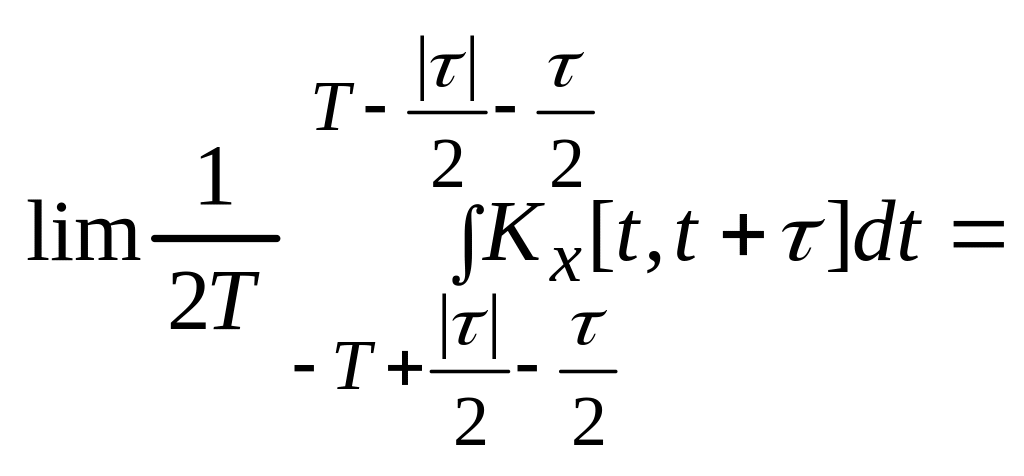|для сигналов II-ой группы этот предел существует |=

= - функция корреляции 2-го рода

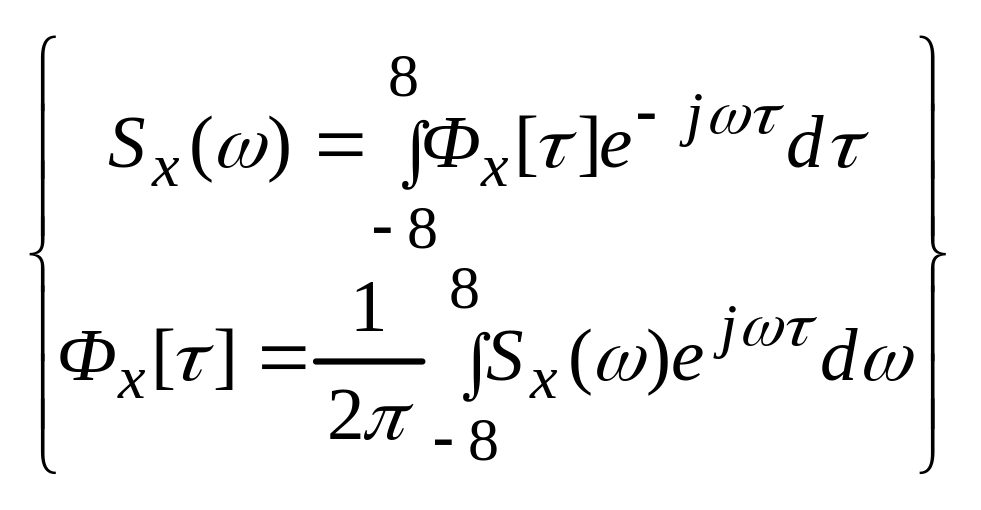
Если сигнал стационарный, то

обладает всеми «К» свойствами.

3. Классификация случайных процессов по их вероятностному последействию. Совершенно случайные процессы и марковские процессы, их описание. Уравнение Смолуховского для условной плотности вероятности марковского процесса.

1. Def. Совершенно случайный процесс (ССП) – процесс, значения которого в несовпадающие моменты времени стат. независимы, т.е.

Т.е. для полного описания нужно знать только одномерную плотность вероятности W(x,t).

Пусть _сист – реакция какой-либо системы на  функцию, а _изм – характерное время изменения сигнала. Тогда если процесс меняется гораздо быстрее, чем может реагировать на то система (_сист >>_изм), то считаем процесс ССП.

2. Def. Случайный процесс x(t) называется марковским (МСП), если для  упорядоченных n моментов времени t₁<t₂<….<t_n условные плотности вероятности данного СП зависят только от последнего условия:

Тогда связь безусловных и условных плотностей вероятности, учитывая условие марковости, принимает вид:

Т.е. для полного описания МСП надо знать W(x₁t₁) и W(x₂t₂| x₁t₁) – вероятность перехода.

МПС – на будущее влияет только настоящее У МСП нет производной – это ССП, т.е. производная меняется случайно.

Уравнение Смолуховского

Пусть есть два момента времени – t₀ и t. Вероятность перехода x₀x: .

Теперь возьмём третий момент времени t₁, лежащий между t₀ и t. Тогда

событие А: x₀x₁:

событие B: x₁x: /

В силу условия марковости события A и В стат. независимы, тогда

. Подсчитаем переход с учётом :

событие С: x₀x: .

Получаем интегральное уравнение:

- ур-ие Смолуховского

1. справедливо для  МСП

2. это ур-ие не решается

3. из него получаются все остальные уравнения для МСП.

4. Детерминированные и квазидетерминированные процессы, их описание в рамках теории случайных процессов, выражения для n-мерных плотностей вероятности.

x(t) = S(t) – детерминированная функций времени.

Замечание: описывать детерминированный процесс с помощью аппарата обобщённых функций нет смысла, он полностью задаётся s(t).

Def. Квазидетерминированным СП назовём процесс, реализации которого задаются детерминированной функцией времени, содержащей один или несколько случайных параметров.

x(t)=S(t,), где S(t,) – заданная детерминированная функция. Вся квазидетерминированность сидит в параметре . W_ () – плотность вероятности случайной непрерывной величины .

Зафиксируем  и найдём условную плотность вероятности (уже для полностью детерминированного процесса).

Тогда по свойству согласованности:

№35. Преобразование спектральной плотности мощности, функции корреляции II-го рода при прохождении случайного процесса через линейную систему.

|

|F^-1

л.с.

Пример:

x(t)=e^jωt

№8. Кумулянтные функции случайного процесса, их связь с характеристической функцией. Связь между кумулянтными и моментными функциями (на примере функций 1-го и 2-го порядка).

Кумулянтные функции вводятся как коэффициенты разложения в ряд Тейлора

Таким образом, задание всех кумулянтных функций эквивалентно заданию n-мерной характеристической функции.

Связь между кумулянтными и моментными функциями произвольного случайного процесса:

S=1

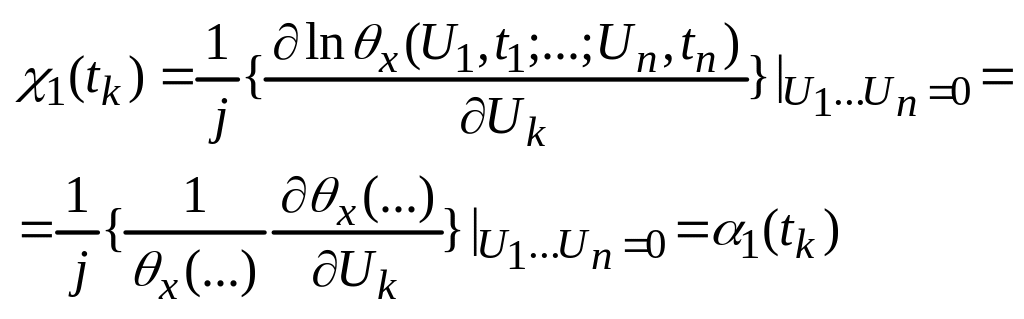
, где и

S=2

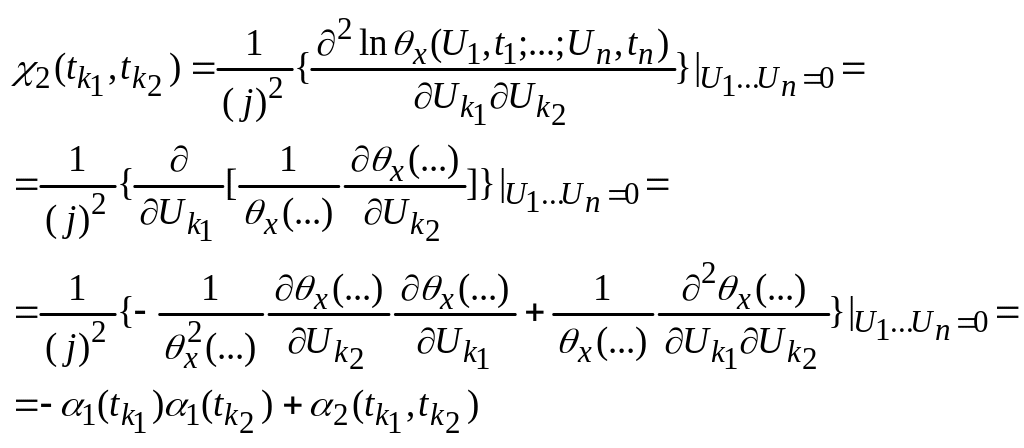, где

, , , ,

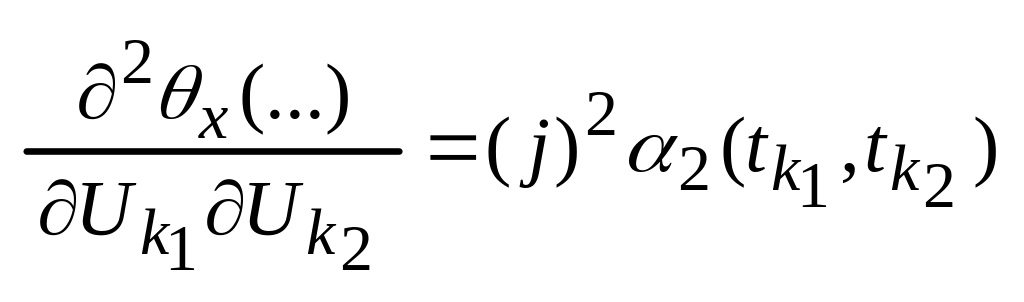Кумулянтная функция S-порядка выражается через моментную функцию S-порядка и моментные функции низших порядков.

№30. Сигналы II-ой группы. Спектральная плотность мощности. Соответствие между спектральной плотностью мощности и корреляционной функцией для стационарных случайных процессов (формула Винера-Хинчина).

x(t) – сигнал II-ой группы, если для него средняя энергия бесконечная, а средняя мощность конечна.

при T→8

x_T(t) – сигнал I-ой группы

при T→8

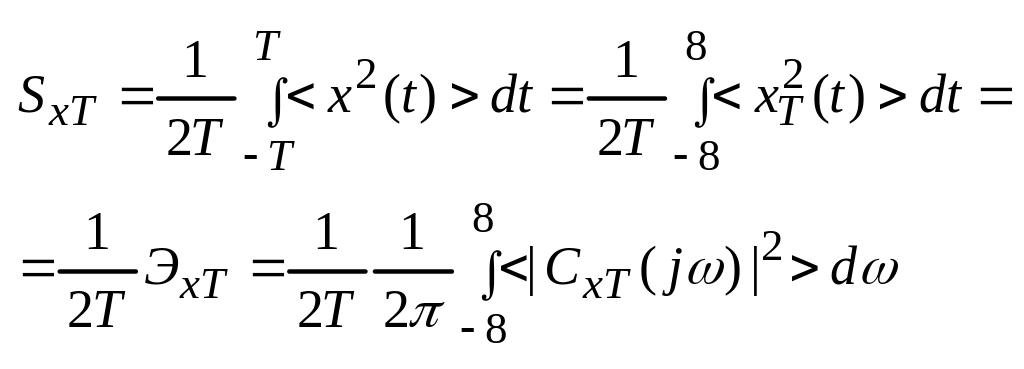
Спектральной плотностью мощности сигнала II-ой группы будем называть предел

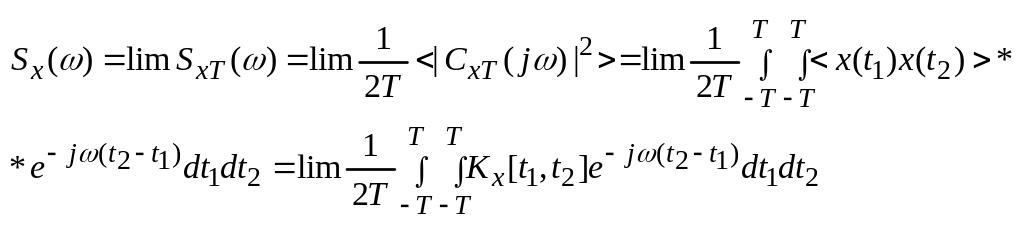
x(t) – стационарный случайный процесс

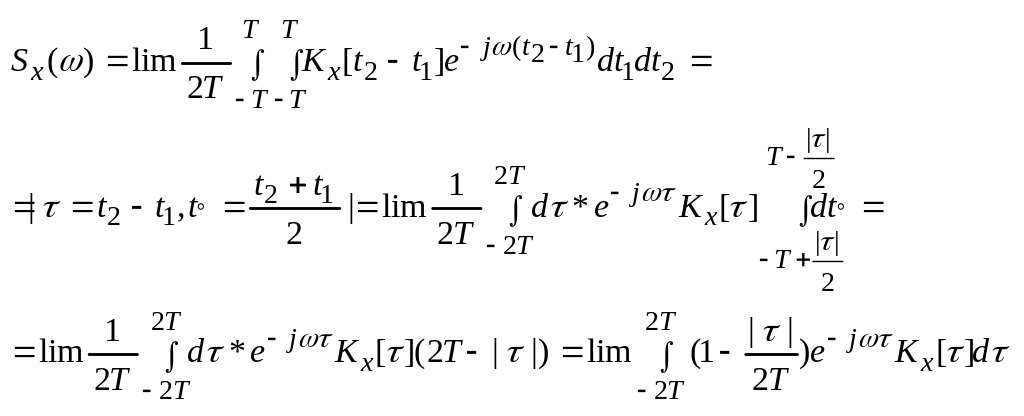
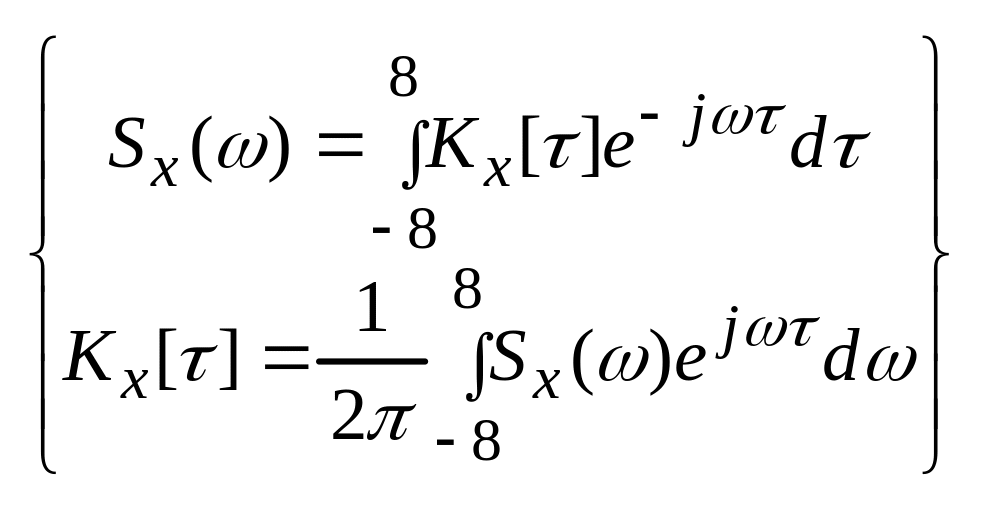- формула Винера-Хинчина

№32. Привести примеры стационарных сигналов II-ой группы (типичных пар: корреляционная функция - спектральная плотность мощности). Как влияет постоянное смещение на вид спектральной плотности мощности случайного процесса.

1)«δ» - дельта корреляционный случайный процесс

2)экспонициальный корреляционный случайный процесс

3)гауссова корреляционная функция

4)

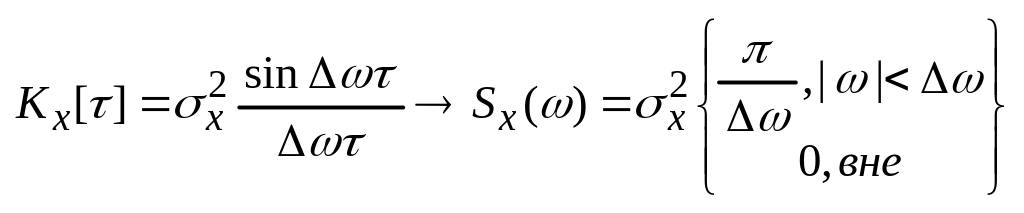
5)

6) ,

,

Влияние среднего значения (постоянного смещения) на вид спектральной плотности мощности случайного процесса

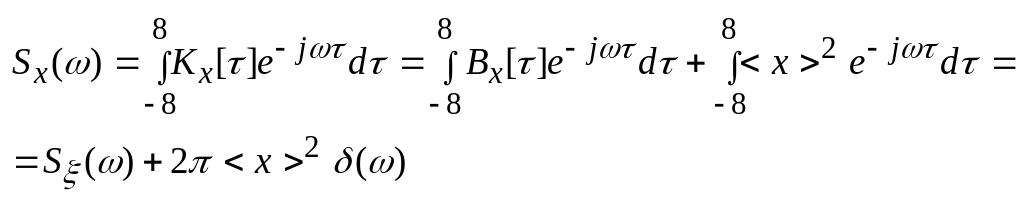
Корреляционная функция смещается вверх по оси y на величину <x>², а на графике спектральной плотности мощности случайного процесса появляется ещё одна составляющая:

№33. Спектральная плотность мощности детерминированного гармонического сигнала, квазигармонического сигнала со случайной фазой и гармонического сигнала, модулированного по амплитуде стационарным случайным процессом.

1) , φ – случайная величина

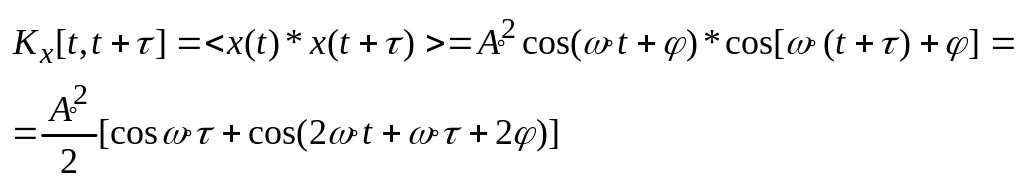
S_x не зависит от φ, поэтому разные случайные детерминированные процессы могут иметь одинаковую спектральную плотность мощности.

2) , ξ(t) – стационарный случайный процесс

время корреляции

№34. Ширина спектра случайного процесса, ее связь со временем корреляции. Узкополосные случайные процессы.

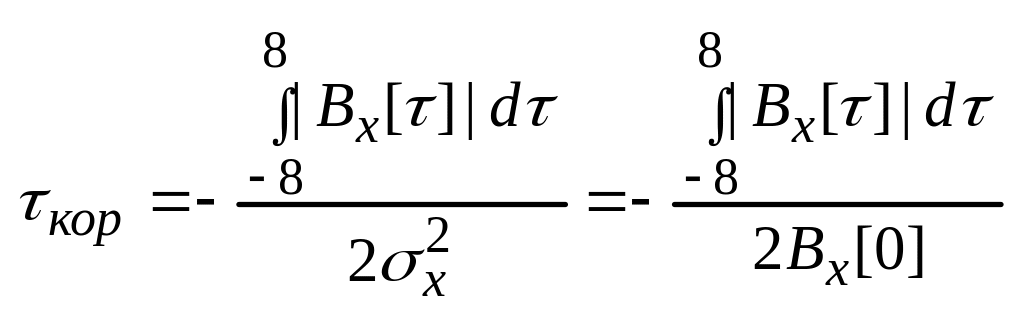
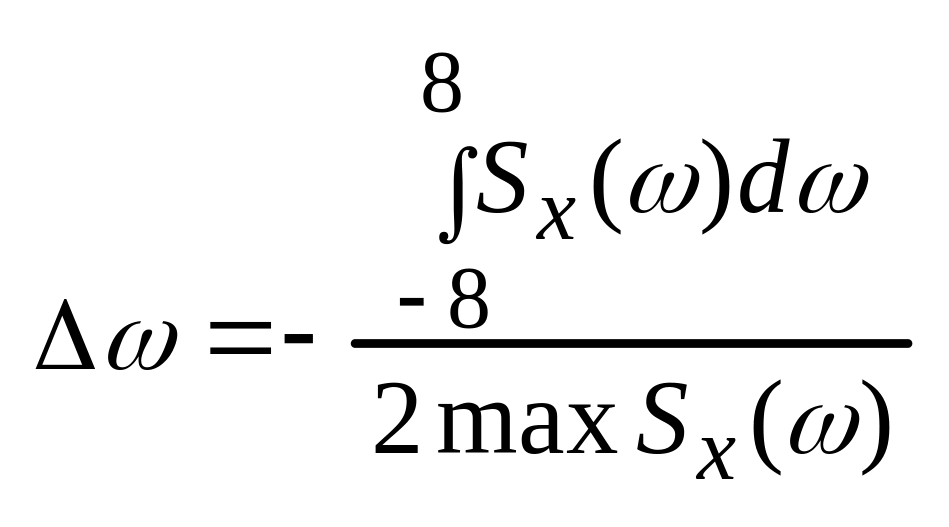
- max достигается в нуле

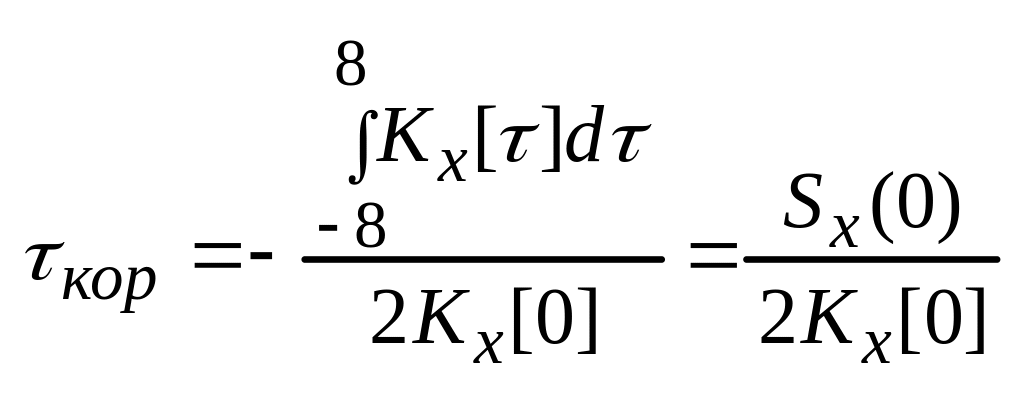
- узкополосные сигналы

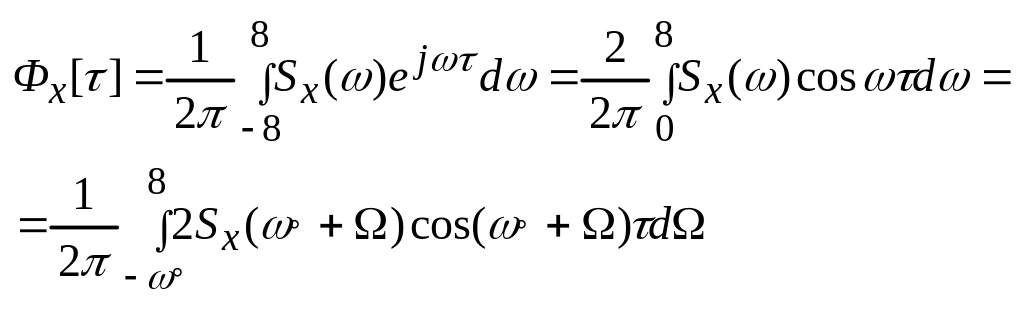
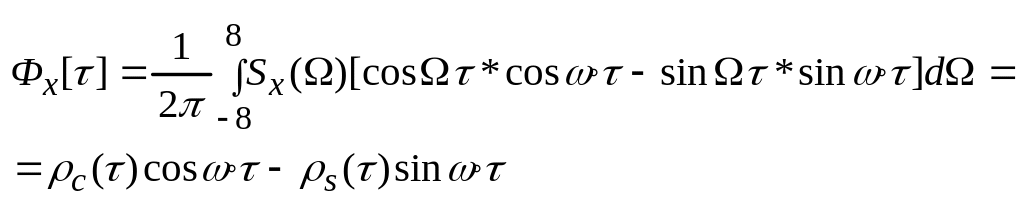
- всегда чётная; если спектр симметричен относительно , то

Рассмотрим узкополосный сигнал , где A(t) и φ(t) – медленные процессы

Данный сигнал можно представить в виде:

, где

- квадратурные компоненты узкополосного случайного процесса

№36. Приближение “белого шума”. Квазистатистическое приближение.

а)

, где - широкая, а - узкая, поэтому

Приближение «белого шума» можно использовать для узкополосной системы

б)

№37. Совместные функции корреляции (I и II-го рода) и спектральные плотности (энергии и мощности). Спектральная плотность мощности на выходе суммирующей цепочки.

{x(t),y(t)}

1) x(t) & y(t) – сигналы первой группы

- взаимная функция корреляции первого рода

а)

б)

(*)

- чётная составляющая взаимной спектральной плотности энергии

- нечётная -//-

2)Сигналы 2-ой группы

x(t) и y(t) – стац. совокупности:

Пример (спектральная плотность мощности на выходе сумматора):

а)x(t)=y(t)

б) x(t)=-y(t)

39. Корреляционная функция спектральных компонент случайного процесса и ее свойства.

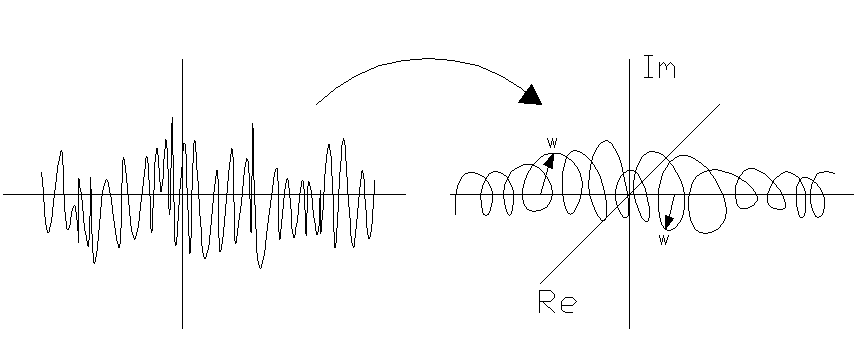
- корр. функция спектральных компонент

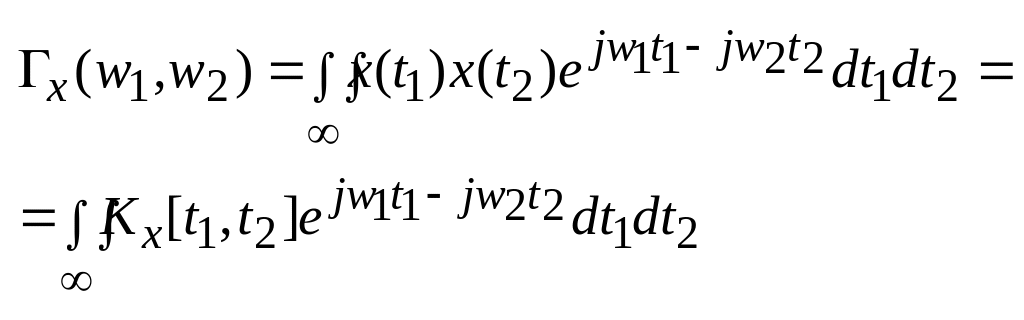
Св-ва:

1)

2)

3)

16.Привести пример стационарного, но неэргодического случайного процесса (статистического ансамбля) с доказательством и обсуждением причин не эргодичности.

x(t)=(t)+A

(t) – стационарный эргодический процесс <(t)> = 0

задана K_ []=B_ []

А – случайная величина с некоторым законом распределения <A>=0

<(t)A> = 0  некоррелированы

является ли x(t) эргодическим ?

B_x []=K_x []=<x(t)x(t+)>=<(t)(t+)>+<A²>+<(t)A>+<(t+)A>= B_ []+<A²>

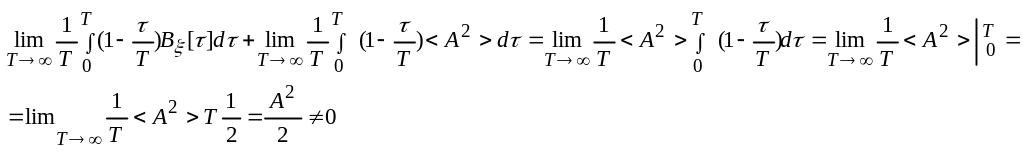
Проверим:  x(t) стационран, неэргод. процесс

= 0, т,к () – эргод.

38. Взаимная спектральная плотность мощности (СПМ) и функция когерентности. Их практическое использование для решения задач технической диагностики.

{x(t),y(t)}

1) x(t) & y(t) – сигналы первой группы

- взаимная функция корреляции первого рода

а)

б)

(*)

- чётная составляющая взаимной спектральной плотности энергии

- нечётная -//-

2)Сигналы 2-ой группы

x(t) и y(t) – стац. совокупности:

(далее аналогично пункту 1 с (*), только заменяй ).

3) , =>

Пример:

=>

в)

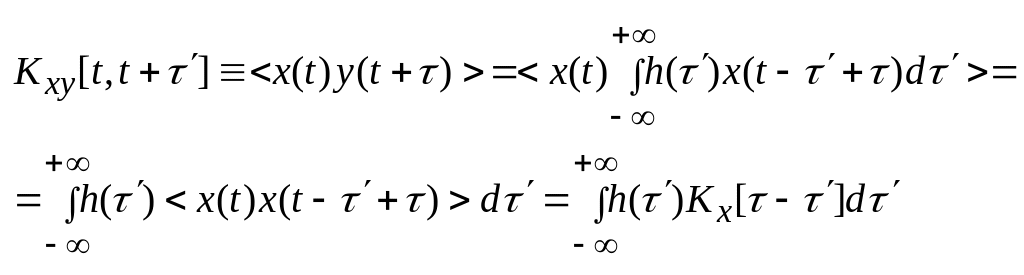
=> - взаимная СПМ входа и выхода.

Обратная задача:

г) св-во ограниченности по модулю

- функция когерентности (коэффициент корреляции спектральных компонент).

- не когерентны на w₀;

- некоррелирующие процессы;

- x(t) и y(t) полностью когерентны;

Пример:

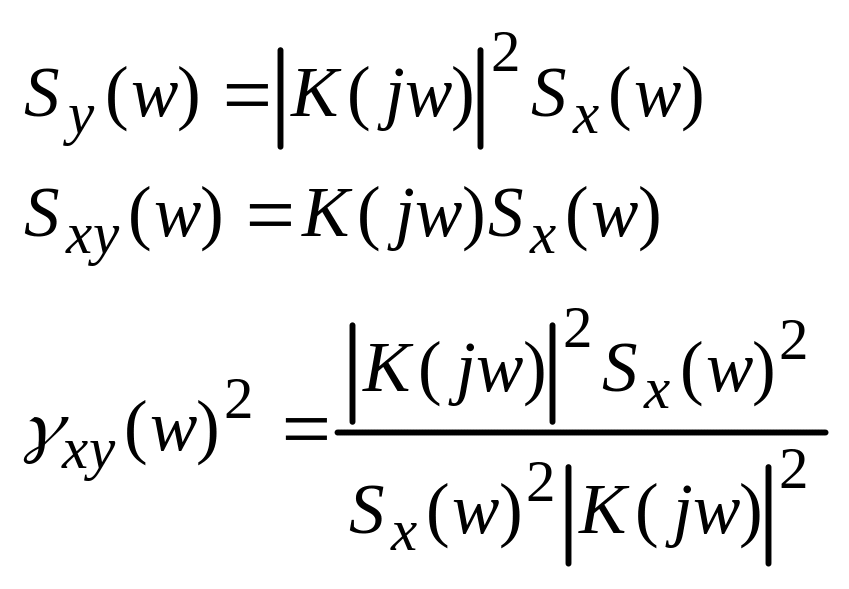
Т.е. для любой ЛС ф-ия когерентности =1. Иначе:

1) система НЛ

2) существует дополнительный источник шума между x(t) и y(t).

40. Корреляционная функция спектральных компонент стационарного случайного процесса, ее выражение через спектральную плотность мощности, взаимная корреляционная функция на выходе двух линейных фильтров, на вход которых подается один и тот же случайный процесс.

x(t) – стац. случайный процесс.

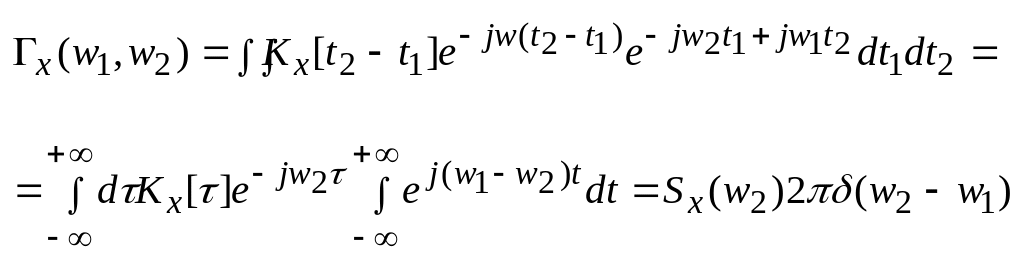
- бесконечный набор дельта-функций огибающая к которым – СПМ.

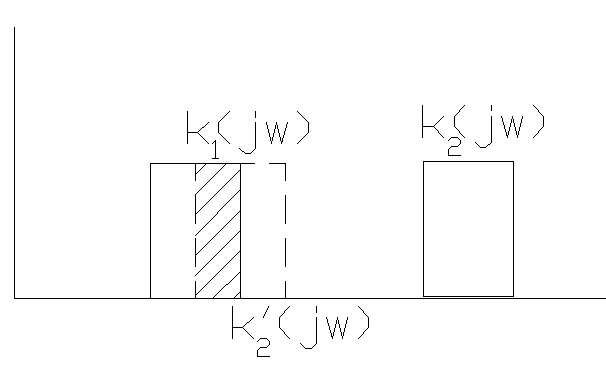
Доказано: . Из формул видно, что если k₁ и k₂ не перекрываются, то взаимная корреляция этих процессов равна нулю. Фильтры вырезают в спектре определённые компоненты. Поэтому если при перекрытии есть одинаковые – получаем ненулевую корреляцию.

17.Необходимые и достаточные условия эргодичности по отношению к корреляционной функции случайного процесса (для произвольного и гауссовского процессов).