2.1.5. Метод электрических изображений

Пусть имеется бесконечная эквипотенциальная плоскость (проводник), над которой задано некоторое распределение зарядов (рисунок 2.2). Требуется определить поле, созданное этими зарядами над плоскостью. Непосредственное определение поля суммированием полей от отдельных зарядов, очевидно, невозможно, так как для этого необходимо знать распределение индуцированных зарядов на самой плоскости.

И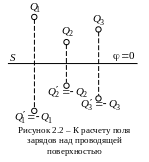 скомое поле должно удовлетворять уравнению Лапласа для всего свободного от зарядов пространства над плоскостью и удовлетворять граничным условиям, а именно: заданным значениям зарядов или потенциалов на заряженных телах и постоянству потенциала на плоскости. Значение потенциала на плоскости можно, не нарушая общности решения, положить равным нулю. Теперь легко видеть, что если взамен индуцированных зарядов, расположенных на плоскости, ввести фиктивные (зеркальные) заряды , , , равные и обратные по знаку

зарядам , , и расположенные симметрично относительно плоскости, то поле, созданное зарядами , , , и фиктивными зарядами , , , будет удовлетворять в верхнем полупространстве тем же граничным условиям, что и поле зарядов , , над проводящей поверхностью, а граничные условия на плоскости удовлетворяются вследствие симметричного расположения относительно плоскости равных по величине и противоположных по знаку зарядов. Введенные фиктивные заряды, позволяющие удовлетворить граничным условиям на плоскости, называются электрическими изображениями истинных зарядов.

Таким образом, метод электрических изображений основан на идее проведения сложной задачи электростатики к более простой задаче с теми же граничными условиями.

2.2. Магнитное поле постоянных токов

Магнитное поле постоянного тока определяется уравнениями:

, , . (2.16)

Для их решения вводится вспомогательная величина – векторный потенциал магнитного поля. В силу тождества

в уравнении полагаем

. (2.17)

Таким образом, задача о нахождении вектора сводится к задаче о нахождении вспомогательного вектора . Однако равенство (2.17) не определяет вектор однозначно, так как для того, чтобы задать поле вектора, надо задать не только его вихрь, но и истоки. Поскольку вектор имеет для нас вспомогательное значение и нам необходимо лишь знание его вихрей, то истоки вектора можно задать произвольно. Нам удобно будет положить, что

. (2.18)

Из (2.17) имеем

.

Подставляя в уравнение

,

получаем

.

На основании тождества

и учитывая (2.18) получаем

. (2.19)

Уравнение (2.19) является уравнением Пуассона в векторной форме.

Решение уравнения Пуассона для скалярного потенциала

имеет вид

.

По аналогии с ним решение уравнения (2.19) будут подобным

. (2.20)

Объем охватывает все области, где плотность токов отлична от нуля.

Если ток протекает по проводнику, диаметр которого мал по сравнению с расстоянием в выражении (2.20), ток можно считать линейным, протекающем по тонкой нити. Тогда в результате интегрирования по поперечному сечению получаем , и формула для векторного потенциала принимает вид

, (2.21)

где – элемент контура с током.

Определив вектор , с помощью формулы

находят напряженность магнитного поля. Если магнитное поле создается контуром с током , то индуктивность этого контура будет равно отношению собственного магнитного потока , пронизывающего контур, к току

.

Для второго контура с током его собственная индуктивность рассчитывается аналогично

.

Отношение магнитного потока , пронизывающего контур , к вызвавшему его току в контуре , называется взаимной индуктивностью между контурами 1 и 2

,

аналогично

.

Взаимные индуктивности равны между собой. Сосредоточенные параметры и определяют связь электрических цепей с созданным ими в окружающем пространстве магнитным полем и рассчитываются методами теории стационарных полей.