28

02129 Статистика вариант 026

Содержание

Задание 1 3

Задание 2 16

Задание 3 21

Задание 4 23

Задание 5 25

Задание 6 26

Задание 1

Определить значения признаков, используя цифры номера зачетной книжки. Результаты определения исходных данных приведены в таблице 1.

Таблица 1 – Исходные данные по выборочной совокупности

Предприятие	факторный Х	результативный У
1	76	6337
2	54	4899
3	58	6736
4	42	3918
5	72	7520
6	86	8585
7	96	8486
8	56	5152
9	117	9999
10	64	5509
11	62	7155
12	32	3675
13	40	3803
14	914	9990
15	74	6076
16	42	4640
17	776	6835
18	59	5327
19	66	7676
20	42	4453
21	74	8167
22	87	9007
23	93	8363
24	60	5702
25	102	9896
26	72	6161
27	66	7093
28	37	4269
29	47	4221
30	90	9995

1. Провести статистическую группировку 30 предприятий по двум признакам и в соответствии с вариантом.

Проведем ранжирование данных таблицы 1 по факторному признаку Х. Результат ранжирования по Х приведен в табл. 2. Здесь же определим минимальные и максимальные значения факторного и результативного признаков. Результат ранжирования по У приведен в табл. 3.

Рассчитываем длины интервалов для факторного и результативного признаков и выделяем группы фирм. Длина интервала для каждого признака определяется по формуле Стерджесса

n = 1 + 3,322 lg N = 1 + 3,322 lg 30 = 5,907,

где n и N - число групп и единиц в статистической совокупности соответственно.

Округляя, принимаем n = 6. Тогда

i_x = = = = 147, i_y = = = = 1054.

Таблица 2 – Ранжирование по Х Таблица 3 – Ранжирование по У

Таблица 3

Факторный, X	Резултативный, Y		Фирма		Факторный, X	Резкльтативный, Y		Фирма
32	3675		12		32	3675		12
37	4269		28		40	3803		13
40	3803		13		42	3918		4
42	3918		4		47	4221		29
42	4640		16		37	4269		28
42	4453		20		42	4453		20
47	4221		29		42	4640		16
54	4899		2		54	4899		2
56	5152		8		56	5152		8
58	6736		3		59	5327		18
59	5327		18		64	5509		10
60	5702		24		60	5702		24
62	7155		11		74	6076		15
64	5509		10		72	6161		26
66	7676		19		76	6337		1
66	7093		27		58	6736		3
72	7520		5		776	6835		17
72	6161		26		66	7093		27
74	6076		15		62	7155		11
74	8167		21		72	7520		5
76	6337		1		66	7676		19
86	8585		6		74	8167		21
87	9007		22		93	8363		23
90	9995		30		96	8486		7
93	8363		23		86	8585		6
96	8486		7		87	9007		22
102	9896		25		102	9896		25
117	9999		9		914	9990		14
776	6835		17		90	9995		30
914	9990		14		117	9999		9
32	3675	минимумы по столбцу
914	9999	максимумы по столбцу
118,53	6654,83	общие средние по столбцу

По найденным значениям длин интервалов рассчитываем границы интервалов. Нижняя граница первого интервала должна быть равна минимальному значению соответствующего признака. Верхняя граница первого интервала факторного признака равна сумме его нижней границы и длины интервала i_x , а верхняя граница первого интервала результативного признака равна сумме его нижней границы и длины интервала i_y . Нижняя граница второго интервала равна верхней границе предыдущего интервала данного признака. Верхняя граница второго интервала больше его нижней границы на длину интервала и т.д. Результаты расчетов представлены в табл. 4 и 5.

Центры интервалов X_{ц к} для расчета общей средней рассчитываем как полусуммы границ соответствующих интервалов. Далее подсчитывается число фирм f_k , попавших в k-ый интервал и средние групповые значения Combin_k (отдельно для каждой из групп – по данным фирм, входящих в группу). Последние два столбца являются вспомогательными для расчета общей средней величины признаков двумя способами: как взвешенной по средним групповым и как взвешенной по центрам интервалов.

Таблица 4 – Границы интервалов по факторному признаку (при Х_мин = 32)

	Границы по Х		Центр	Число	Среднее
Группа	нижняя	верхняя	инт. Xц к	фирм fk	Combink	Combink*fk	Xц к*fk
1	32,00	179,00	105,50	28	66,64	1866	2954,00
2	179,00	326,00	252,50	0	–	0	0,00
3	326,00	473,00	399,50	0	–	0	0,00
4	473,00	620,00	546,50	0	–	0	0,00
5	620,00	767,00	693,50	0	–	0	0,00
6	767,00	914,00	840,50	2	845,00	1690	1681,00
Сумма	-	-	-	30	-	3556	4635,00

Таблица 5 – Границы интервалов по результативному признаку (при У_мин = 3675)

	Границы по У		Центр	Число	Среднее
Группа	нижняя	верхняя	инт. Уц к	фирм fk	Combink	Combink*fk	Уц*fk
1	3675,00	4729,00	4202,00	7	4139,86	28979	29414,00
2	4729,00	5783,00	5256,00	5	5317,80	26589	26280,00
3	5783,00	6837,00	6310,00	5	6429,00	32145	31550,00
4	6837,00	7891,00	7364,00	4	7361,00	29444	29456,00
5	7891,00	8945,00	8418,00	4	8400,25	33601	33672,00
6	8945,00	9999,00	9472,00	5	9777,40	48887	47360,00
Сумма	-	-	-	30	-	199645	197732,00

В случае если заполнение групп неравномерное, рекомендуется произвести перегруппировку таким образом, чтобы в каждую группу попало приблизительно одинаковое количество фирм. Результаты перегруппировки приведены в табл. 6 и 7.

Таблица 6 – Границы интервалов по факторному признаку

(перегруппировка при Х_мин = 32)

	Границы по Х		Центр	Число	Среднее
Группа	нижняя	верхняя	инт. Xц к	фирм fk	Combink	Combink*fk	Xц к*fk
1	32	40	36	2	34,50	69	72
2	40	45	42,5	4	41,50	166	170
3	45	70	57,5	10	59,20	592	575
4	70	90	80	7	77,29	541	560
5	90	767	428,5	5	99,60	498	2142,5
6	767	914	840,5	2	845,00	1690	1681
Сумма	-	-	-	30	-	3556	5200,5

Таблица 7 – Границы интервалов по результативному признаку

(перегруппировка при У_мин = 3675)

	Границы по У		Центр	Число	Среднее
Группа	нижняя	верхняя	инт. Уц к	фирм fk	Combink	Combink*fk	Уц*fk
1	3675	4729	4202	7	4139,86	28979	29414
2	4729	5783	5256	5	5317,80	26589	26280
3	5783	6837	6310	5	6429,00	32145	31550
4	6837	7891	7364	4	7361,00	29444	29456
5	7891	8945	8418	4	8400,25	33601	33672
6	8945	9999	9472	5	9777,40	48887	47360
Сумма	-	-	-	30	-	199645	197732

На основе таблиц 4-5 и 6-7 строится комбинационная группировка (см. табл. 8 и 9), где каждая группа, полученная по факторному признаку, разбивается на подгруппы по результативному признаку.

Таблица 8 - Комбинационная таблица по равным интервалам

Группы по Х			Группы по У
Номер			1	2	3	4	5	6
	Границы		нижняя						Кол-во
			3675	4729	5783	6837	7891	8945
	нижняя	верхняя	4729	5783	6837	7891	8945	9999
1	32,00	179,00	7	5	4	4	4	4	28
2	179,00	326,00							0
3	326,00	473,00							0
4	473,00	620,00							0
5	620,00	767,00							0
6	767,00	914,00			1			1	2
Итого фирм в группе			7	5	5	4	4	5	30

Таблица 9 - Комбинационная таблица по интервалам после перегруппировки

Группы по Х			Группы по У
Номер			1	2	3	4	5	6
	Границы		нижняя						Кол-во
			3675	4729	5783	6837	7891	8945
	нижняя	верхняя	4729	5783	6837	7891	8945	9999
1	32	40	2						2
2	40	45	4						4
3	45	70	1	5	1	3			10
4	70	90			3	1	2	1	7
5	90	767					2	3	5
6	767	914			1			1	2
Итого фирм в группе			7	5	5	4	4	5	30

2. Рассчитать общие средние величины по факторному и результативному признакам разными способами: как простые средние арифметические, как средневзвешенные из групповых средних, как средневзвешенные из середин интервалов. Выявить преимущества и недостатки этих способов с точки зрения точности получения результатов, простоты и эффективности проведения расчетов в макроэкономических исследованиях.

Групповые средние величины рассчитываются отдельно для каждой из групп по данным фирм, входящих в группу

Combin_k = , Combin_k = .

где k – номер группы (интервала); j – номер предприятия в k-ом интервале.

Результаты расчета групповых средних арифметических для признаков Х и У приведены в 6-ых столбцах таблиц 4-7.

Находим общие средние по каждому изучаемому признаку (данные для расчетов и результаты промежуточных вычислений приведены в таблицах 4-7, 13):

• на основе простой средней арифметической (истинная средняя)

Combin_общ = 118,53 т.р., Combin_общ = 6654,83 чел.;

• по формуле взвешенной из средних групповых

Combin\s\up 4( груп = = 3556/30 = 118,53 т.р.,

Combin\s\up 4( груп = = 199645/30 = 6654,83 чел.;

• по формуле взвешенной из середин интервалов каждой группы

Combin\s\up 4( центр = = 5200,5/30 = 173,35 т.р.,

Combin\s\up 4( центр = = 197732/30 = 6591,07 чел.,

где i - номер фирмы ( i = 1,2,...30); k - номер группы; f _k - число фирм в k-ой группе.

Видим, что значения общих средних, найденных на основе простой средней арифметической и по формуле взвешенной из средних групповых совпадают, что следует из выражений, по кото­рым они определяются. Это свидетельствует о высокой точности вычисления общих средних по формуле взвешенной из средних групповых (здесь могут возникать незначительные расхождения из-за округлений промежуточных результатов – средних групповых значений), а также о том, что групповые и общие средние величины найдены правильно.

Погрешности расчетов общих средних по формуле взвешенной из середин интервалов составят:

δ_х = (Combin\s\up 4( центр - Combin_общ) ·100 / Combin_общ = (173,35 - 118,53) ·100 / 118,53 = 46,25 %,

δ_у = (Combin\s\up 4( центр - Combin_общ) ·100 / Combin_общ = (6591,07 - 6654,83) ·100 / 6654,83 = -0,96 %.

Обобщая результаты расчета средних величин можно сделать вывод, что самый простой способ нахождения значений общих средних – расчет по формуле взвешенной из середин интервалов каждой группы (при его использовании значительно сокращается объем вычислений, т.к. не требуется ни расчета среднегрупповых значений (формула взвешенной из средних групповых), ни довольно ресурсоемкой работы по суммированию всех исходных данных(формула простой средней арифметической)). Однако, из-за несовпадения значений центров интервалов и среднегрупповых значений этот способ может давать результаты с относительно высокой погрешностью. Поэтому его применение там где требуется высокая точность должно быть ограничено.

3. По факторному признаку рассчитать структурные средние: моду и медиану. Проверить величину моды графическим способом. Оценить симметричность распределения факторного признака по местоположению моды, медианы и средней арифметической величины.

Мода – наиболее часто встречающееся значение признака. В интервальном ряду сначала определяется модальный интервал, то  есть тот интервал, который имеет наибольшую частоту (подсчет групповых и накопленных частот приведен в табл. 10).

Таблица 10 – Группировочная таблица для расчета накопленных частот

по факторному признаку

	Границы по Х		Число	Накопленная
Группа	нижняя	верхняя	фирм fk	частота, Sk
1	32	40	2	2
2	40	45	4	6
3	45	70	10	16
4	70	90	7	23
5	90	767	5	28
6	767	914	2	30

В данном случае – интервал [45; 70). Конкретное значение моды определяется по формуле

,

где ХМо =	45,00	– нижняя граница модального интервала;
i =	25,00	– величина модального интервала;
fМо =	10	– частота модального интервала;
fМо -1 =	4	– частота интервала, предшествующего модальному;
fМо+1 =	7	– частота интервала, следующего за модальным.

Мо = 45 + 25 · = 61,67 т.р.

Медиана соответствует варианту, стоящему в середине ранжированного ряда. Место медианы

В интервальном ряду распределения сначала указывают интервал, в котором находится медиана. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений – интервал [45; 70). Численное значение медианы определяется по формуле

,

где ХМе =	45,00	– нижняя граница медианного интервала;
i =	25,00	– величина медианного интервала;
SМе -1 =	6	– накопленная частота интервала, предшествующего медианному;
fМе =	10	– частота медианного интервала.

Ме = 45 + 25 · = 67,5 т.р.

На основании этих результатов можем утверждать, что фирмы имеющие среднегодовую стоимость ОФ равную 61,67 т.р. будут встречаться чаще других и, что количество фирм, имеющих среднегодовую стоимость ОФ меньше и больше 67,5 т.р. будет одинаковым.

Коэффициент асимметрии можно рассчитать по трем формулам с учетом значений моды, медианы и среднего арифметического

;

;

,

где – центральный момент третьего порядка, рассчитывается по формуле

.

Расчет As будем проводить по последней формуле, т.к. она позволяет получить более точный результат при асимметричном распределении, т.е. когда Мо ≠ Ме ≠ Combin_общ.

При левосторонней асимметрии As < 0, при правосторонней асимметрии As > 0, для нормального распределения As = 0.

Асимметрия является значительной, если As > 0,5 по абсолютной величине, при <0,25 ее считают незначительной.

Для симметричных распределений определяется показатель эксцесса Ек

,

где – центральный момент четвертого порядка, равный

.

При островершинном распределении Ек > 0, при нормальном Ек = 0, при плосковершинном распределении Ек < 0.

Степень существенности коэффициента Ек определяют по величине среднеквадратической ошибки

.

Если , значение Ек является существенным. Если , значение Ек является несущественным.

Степень существенности коэффициента As определяют по величине среднеквадратической ошибки

.

Если отношение , асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. В противном случае асимметрия несущественна и может возникнуть под влиянием случайных колебаний признака.

Для расчета коэффициентов асимметрии и эксцесса составим вспомогательную таблицу

Таблица 11 – Вспомогательная таблица для расчета коэффициентов асимметрии и эксцесса

	Границы по Х		Число	Среднее
Группа	нижняя	верхняя	фирм fk	Combink	Combink – Combin	(Combink – Combin)3·fk	(Combink – Combin)4·fk
1	32	40	2	34,50	-84,03	-1186820	99732421
2	40	45	4	41,50	-77,03	-1828505	140855806
3	45	70	10	59,20	-59,33	-2088797	123935291
4	70	90	7	77,29	-41,25	-491241	20262526
5	90	767	5	99,60	-18,93	-33935	642508
6	767	914	2	845,00	726,47	766791114	557048184358
Сумма	-	-	30	-	-	761161816	557433612909

Находим:

- центральный момент третьего порядка

= 761161816/30 = 25372060,53;

- коэффициент асимметрии

= 25372060,53/196³ = 3,37,

больше нуля, следовательно асимметрия правосторонняя. Т.к. > 0,5, асимметрия является значительной.

- среднеквадратическая ошибка

= = 0,412.

Т.к. отношение 3,37/0,412 = 8,18 больше 3, следовательно асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.

Несмотря на несимметричность распределения, с целью выполнения задания находим:

- центральный момент четвертого порядка

= 557433612909/30 = 18581120430,3;

- коэффициент эксцесса

= 18581120430,3/196⁴ – 3 = 9,591,

больше нуля, следовательно распределение островершинное.

- среднеквадратическая ошибка

= = 0,749.

Т.к. = 9,591/0,749 = 12,81 значение Ек является существенным.

Построим гистограмму и кумуляту по факторному признаку. Построения производим на основании данных группировочной таблицы (см. табл. 10). Результаты построений приведены на рис. 2, 3. Там же показаны мода и медиана, найденные графическим способом. По рисункам видно, что значения моды и медианы, найденные графическим способом и расчетным путем совпадают.

Рисунок 1 – Гистограмма распределения фирм по факторному признаку

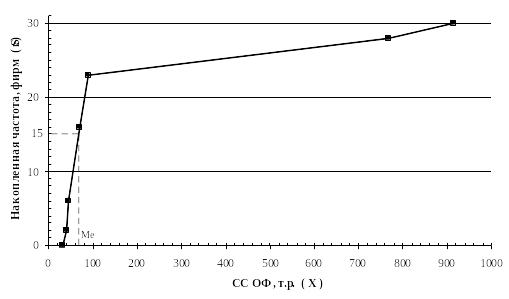
Рисунок 2 – Кумулята распределения фирм по факторному признаку

Проводим расчет средних групповых значений по факторному и результативному признакам (при этом групповые средние по результативному признаку определяются по группам фирм, полученным при группировке по факторному признаку) в абсолютном и относительном выражении. Исходными к расчету являются исходные данные по фирмам, ранжированные по Х (табл. 2). Результаты расчетов приведены в табл. 12. По рассчитанным групповым средним значениям для каждой группы определяем относительные показатели (групповые средние в относительном выражении), при­няв средние значения факторного и результативного признаков первой группы за 100%, по формулам

ОПХ_k = Combin_k ·100 / Combin₁; ОПУ_k = Combin_k ·100 / Combin₁.

Таблица 12 – Относительные величины факторного и результативного признаков

	Границы по Х		Абсолютные значения		Относительные значения, %
Группа	нижняя	верхняя	среднее X к	среднее Ук	ОПXk	ОПУk
1	32	40	34,50	3972,00	100	100
2	40	45	41,50	4203,50	120,29	105,83
3	45	70	59,20	5947,00	171,59	149,72
4	70	90	77,29	7407,57	224,02	186,49
5	90	767	99,60	9347,80	288,70	235,34
6	767	914	845,00	8412,50	2449,28	211,80

Относительные показатели более ярко выражают характер зависимости результативного признака от факторного и позволяют увидеть, прямая она или обратная, либо ее нет. В данном случае из таблицы видно, что с увеличением номера интервала значения факторного признака возрастают, что и должно быть исходя из способа группировки. По результативному же признаку четкой тенденции не наблюдается.

Найденные относительные величины являются относительными показателями координации т.к. характеризуют соотношение отдельных частей целого между собой. В качестве базы сравнения выбраны средние значения факторов Х и У по первой группе фирм.

4. Построить эмпирическую и теоретическую линию регрессии зависимости результативного признака от факторного.

Таблица 13 – Вспомогательная таблица для расчета уравнения регрессии

№	Х	У	Х·У	Х2	(Х – Combin)2	(У – Combin)2	УХ	(УХ – Combin)2
1	2	3	4	5	6	7	8	9
1	76	6337	481612	5776	1809,1	101018,0	6506,2	22081,6
2	54	4899	264546	2916	4164,6	3082950,7	6429,4	50832,2
3	58	6736	390688	3364	3664,3	6588,0	6443,3	44726,0
4	42	3918	164556	1764	5857,4	7490256,7	6387,4	71494,4
5	72	7520	541440	5184	2165,4	748513,4	6492,3	26430,1
6	86	8585	738310	7396	1058,4	3725543,4	6541,2	12919,0
7	96	8486	814656	9216	507,8	3353171,4	6576,1	6197,6
8	56	5152	288512	3136	3910,4	2258508,0	6436,4	47730,3
9	117	9999	1169883	13689	2,4	11183450,7	6649,5	28,7
10	64	5509	352576	4096	2973,9	1312934,0	6464,3	36299,0
11	62	7155	443610	3844	3196,0	250166,7	6457,3	39010,4
12	32	3675	117600	1024	7488,0	8879406,7	6352,5	91398,2
13	40	3803	152120	1600	6167,5	8132953,4	6380,5	75279,9
14	914	9990	9130860	835396	632767,2	11123336,7	9434,0	7723512,2
15	74	6076	449624	5476	1983,2	335048,0	6499,2	24207,0
16	42	4640	194880	1764	5857,4	4059553,4	6387,4	71494,4
17	776	6835	5303960	602176	432262,4	32460,0	8951,8	5276164,7
18	59	5327	314293	3481	3544,2	1763141,4	6446,8	43260,5
19	66	7676	506616	4356	2759,8	1042781,4	6471,3	33685,3
20	42	4453	187026	1764	5857,4	4848070,0	6387,4	71494,4
21	74	8167	604358	5476	1983,2	2286648,0	6499,2	24207,0
22	87	9007	783609	7569	994,4	5532688,0	6544,7	12137,0
23	93	8363	777759	8649	652,0	2917833,4	6565,6	7957,7
24	60	5702	342120	3600	3426,2	907891,4	6450,3	41819,4
25	102	9896	1009392	10404	273,4	10505161,4	6597,1	3336,5
26	72	6161	443592	5184	2165,4	243871,4	6492,3	26430,1
27	66	7093	468138	4356	2759,8	191990,0	6471,3	33685,3
28	37	4269	157953	1369	6647,7	5692200,7	6370,0	81141,2
29	47	4221	198387	2209	5117,0	5923544,7	6404,9	62458,0
30	90	9995	899550	8100	814,2	11156713,4	6555,1	9937,5
Сумма	3556	199645	27692226	1574334	1152829	119088394	-	14071355

На основе анализа графика зависимости результативного признака от факторного (см. рис. 3), построенного по средним групповым данным (4-й и 5-й столбцы табл. 12), то есть эмпирической линии регрессии (ломаная линия) предполагаем, что между исследуемыми признаками существует линейная зависимость (здесь же представлено корреляционное поле зависимости результативного признака от факторного построенное по данным табл. 1).

Рисунок 3 – Корреляционное поле и линии регрессии

Поэтому теоретическую линию регрессии ищем в виде прямой y = a + b x,

где коэффициенты а и b определяем по методу наименьших квадратов для исходных данных по формулам (промежуточные расчеты приведены в табл. 13)

, ,

где N = 30 – объем выборки; Combin = 118,53 т.р. и Combin = 6654,83 чел. – средние значения факторов.

Вычисляя, получаем

a =

######

b =

3,4937

Полученное теоретическое уравнение прямой регрессии имеет вид

У = 0 +3,4937 ·Х.

По этому уравнению вычисляем теоретические значения результативного признака для значений Х_min = 32 и Х_max = 914:

У_Х(32) = 111,798; У_Х(914) = 3193,242.

Пользуясь этими значениями, строим теоретическую линию регрессии (прямая линия на рис. 3).

5. Определить показатель тесноты связи между признаками и коэффициенты вариации. Сделать выводы о тесноте связи между признаками и степени однородности статистической совокупности по этим признакам.

Т.к. была выбрана прямая линия регрессии, то в качестве показателя тесноты связи рассчитываем коэффициент корреляции, предварительно определив среднеквадратические отклонения Х и У (промежуточные вычисления – в табл. 13):

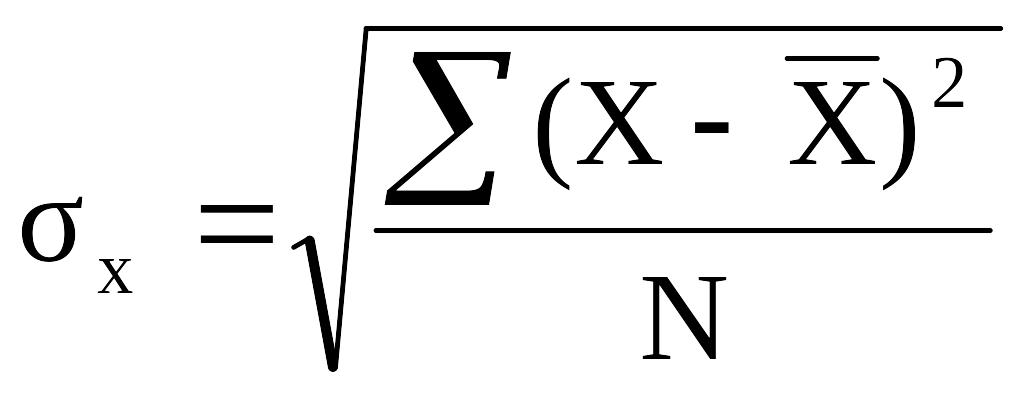= = 196,0; = = 1992,4,

= = 0,3439.

В качестве показателя тесноты связи также используют теоретическое корреляционное отношение (оно может применяться и для нелинейных зависимостей):

= = 0,3437,

где У_Х – выравненные значения результативного признака, то есть рассчитанные по уравнению регрессии У = 0 +3,4937 ·Х (приведены в табл. 13 графа 8).

Воспользовавшись шкалой Чеддока, делаем вывод, что между исследуемыми признаками есть слабая корреляционная связь.

Для проверки значимости коэффициента корреляции найдем расчетное значение коэффициента Стьюдента

= 0,3439· = 1,938.

По статистическим таблицам находим критическое значение критерия Стьюдента при уровне значимости  = 0,05 и числе степеней свободы N – 2 = 28

t_кр = 2,048.

Т.к. t_r < t_кр, то значение коэффициента корреляции признаем не значимым и делаем вывод об отсутствии корреляционной связи между признаками.

Расчет коэффициента детерминации проводим по формулам

D = r ² или D =  ².

D = 0,3439² = 0,1183.

Коэффициент детерминации показывает, какая доля изменчивости результативного признака обусловлена изменчивостью факторного признака, т.е. в данном случае эта доля составляет 11,83%.

Рассчитываем коэффициенты вариации для факторного и результативного признаков как отношение среднеквадратического отклонения к соответствующей средней арифметической:

= ·100 % = 165,36 %, что больше 33 %,

следовательно, статистическая совокупность значений по признаку Х не однородна;

=  100 % = 29,94 %, что меньше 33 %,

следовательно, статистическая совокупность значений по признаку Y однородна.

6. С вероятностью Р, заданной в таблице 3, определить возможные пределы изменения общих средних величин факторного и результативного признаков, найденных выше. При этом следует учесть, что выборка, состоящая из 30 предприятий, получена из генеральной совокупности путем 10%-го случайного бесповторного отбора.

P =

0,9907

t =

2,6

С вероятностью Р = 0,9907 определим возможные пределы изменения средних величин факторного и результативного признаков для генеральной совокупности при условии, что данные по 30 предприятиям получены путем 10%-го случайного бесповторного отбора.

Доверительный интервал для генеральной средней Combin_ген

Combin_выб – ∆_х ≤ Combin_ген ≤ Combin_выб + ∆_х,

где Combin_выб – средний уровень признака Х по выборке;

∆_х = t · μ_х – предельная ошибка выборки;

t – коэффициент кратности средней ошибки выборки, определяемый по статистическим таблицам. При Р = 0,9907 t = 2,6;

μ_х – средняя ошибка выборки, которая для случая случайного бесповторного отбора определяется по формуле

,

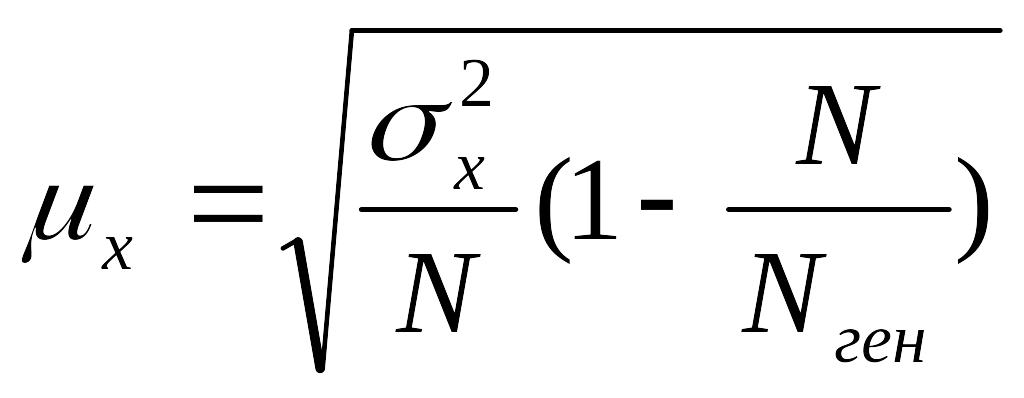где = 0,1 – отношение объема выборки к объему генеральной совокупности.

Имеем: N = 30; Combin_выб = 118,53; _х = 196; Combin_выб = 6654,83; _у = 1992,4.

Находим:

∆_х = t · μ_х = t · = 2,6 · = 88,27;

∆_у = t · μ_у = t · 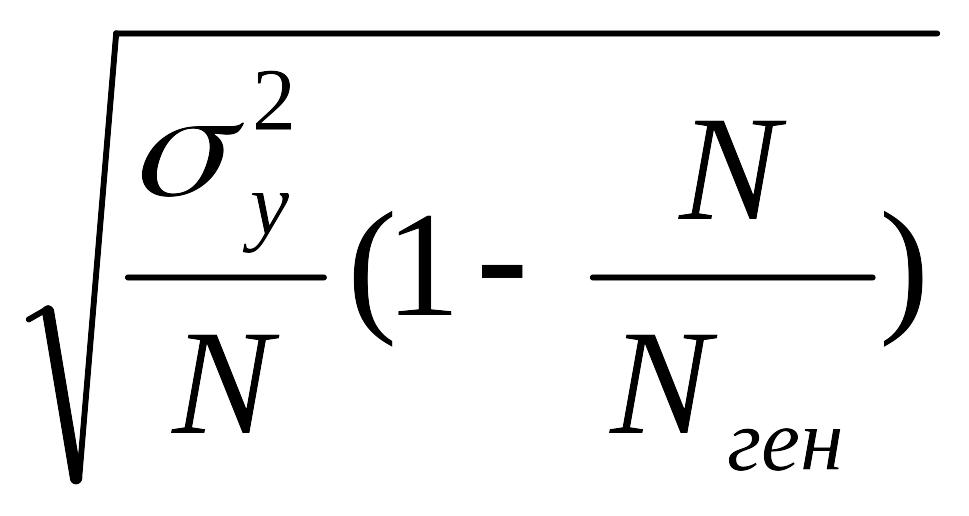= 2,6 · = 897,24.

Таким образом, с вероятностью 0,9907 мы можем утверждать, что среднее значение признака Х для генеральной совокупности будет находиться в интервале

[30,26; 206,8] т.р., а признака Y – в интервале [5757,59; 7552,07] чел.