37. Транспортная задача: основные понятия, постановка, математическая модель.
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
Математическая модель транспортной задачи
Переменными (неизвестными) транспортной задачи являются xij , i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок:
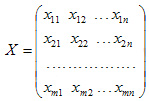
Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:
По условию
задачи требуется обеспечить минимум
суммарных затрат.
Следовательно,
целевая функция задачи имеет вид:
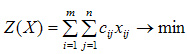
Система
ограничений задачи состоит из двух
групп уравнений.
Первая группа из m
уравнений описывает тот факт, что запасы
всех m поставщиков вывозятся полностью
и имеет вид:
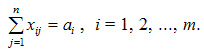
Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:
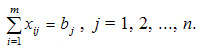
Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом:
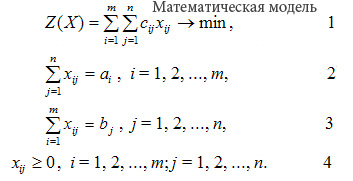
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарынм запросам потребителей, т.е.:
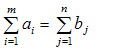
Такая задача называется задачей с правильным балансом, а модель задачи закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи — открытой.
38. Построение начального плана транспортной задачи, критерий оптимальности плана.
Лемма:
Максимальное количество линейно независимых столбцов матрицы А = m+n-1
Следствие:
Число положительных компонентов базисного плана транспортной задачи не превосходит А.
Классическая транспортная задача является закрытой моделью. Мощность = емкость. В этом случае все ограничения задачи являются равенствами.
Все дальнейшее относится только к закрытой транспортной задаче.
Если базисный план содержит ровно m+n-1 положительных компонентов, то такая задача называется невырожденной. Для решения такой задачи применяется метод решения потенциалов.
Задача всегда имеет решение и причем может иметь несколько.
Для того чтобы начать метод потенциалов, нужно построить начальный базисный план:
Метод северо-западного угла.
Заполнение плана перевозок начинается с верхнее левого угла последовательными разгрузками каждого поставщика. При этом используется принцип максимальной отгрузки, то есть на каждом шаге поставщики разгружаются с максимальной эффективностью.
Метод наименьшей стоимости
Заполнение плана перевозок начинается с элемента с наименьшей ценой, дальнейший процесс идет по возрастанию цен перевозок, притом так же используется принцип максимальной отгрузки. Если имеется несколько элементов с одинаковой емкостью, разгружать надо того поставщика, у которого будет вывезена наибольшее количество продукции.
Критерий оптимальности транспортной задачи
План перевозок
является оптимальным планом тогда и только тогда, когда найдется система платежей
для которой выполняются условия :
