Вопрос 29. Задача линейного программирования: математическая модель и основные понятия.

Математическая модель

Этапы построения любой математической модели задачи линейного программирования:

1. определение неизвестных (переменных)

2. ввод ограничений задачи

3. ввод целевой функции для ее оптимизации

Основная структура математической модели:

где n – виды продукции, m – виды ресурсов, b – ограничения

Основные понятия

Любой набор переменных X, удовлетворяющий всем ограничениям задачи, есть допустимое решение и является планом задачи.

План, на котором достигается оптимальное значение целевой функции – оптимальный план.

Так как все переменные находятся в первой степени, то это задача линейного программирования.

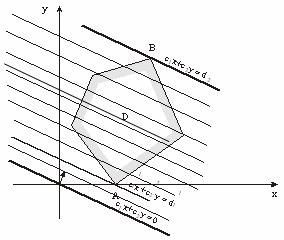
30. Графическое решение злп.

Решение задачи линейного программирования графическим методом включает следующие этапы:

1. На плоскости X10X2 строят прямые.

2. Определяются полуплоскости.

3. Определяют многоугольник решений;

4. Строят вектор N(c1,c2), который указывает направление целевой функции;

5. Передвигают прямую целевую функцию c1x2 + c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.

6. Вычисляют координаты точки и значение целевой функции в этой точке.

31. Симплекс-метод: каноническая форма задачи, базисный план, заполнение первой симплекс-таблицы.

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан математиком Джорджем Данцигом в 1947 году.

Задача называется задачей в канонической форме если:

1. b_j ≥ 0 для любых j принадлежащих 1:m

2. в каждом ограничении кроме знаковых содержится базисная переменная, т.е. переменная входящая только в этом ограничении с коэффициентом 1.

Переменные, не являющиеся базисными, называются свободными.

Приведение задачи в канон. Форму:

1. избавляемся от отрицательной правой части

2. избавление от знака неравенства с помощью введения доп. Переменных.

Базисный план – это план задачи, в котором все свободные переменные равны нулю.

Предположим после всех преобразований мы получили задачу с естественным базисом, то есть является в канонической форме и можно применять метод. Каждый шаг метода отображается в последовательности симплекс-таблицах.

1.Каждому ограничению соответствует строка СТ, а целевой ф-ции соответствует последняя строка, к-ая называется индексной строкой.

2.В первом столбце СТ записываются переменные, к-ые явл-ся базисными для соответствующего ограничения, а во втором записываются их значения.

3.Последний элемент 2ого столбца указывает на значение целевой ф-ции на данном базисном плане задачи.

32. Симплекс-метод: теорема об индексной строке, пересчет симплекс-таблицы.

Правило заполнение индексной строки

1.если целевая ф-ция не содержит базисных переменных, тогда в индекс строку заносятся коэф-ты целевой функции, при этом свободные заносятся со своим знаком, а остальные с противоположным.

2. если целевая функция содержит базисные переменные, тогда индексная строка заполняется по правилу цен: слева и сверху от таблицы выписываются коэффициенты при переменных целевой ф-ции. Каждый элемент индексной строки есть произведение столбца цен слева на соответствующий столбец СТ + цена наверху для первого столбца и – цена наверху для всех остальных.

Проверка базисного плана на оптимальность:

Теорема:

1. если все элементы индекс строки исключая первой не отрицательны, то базисный план является оптимальным, а 1ый элемент содержит оптимальное значение целевой ф-ции.

2. Если среди элементов индекс. строки есть отрицательные исключая первой, а в столбах над ними нет ни одного положительногоэлемента, то задача не имеет решение, так как целевая фу-ция не ограничена сверху на множестве планов.

3. Если в индекс строке имеются отриц элементы исключая первой и в столбцах над ними есть хотя бы один положительный элемент, то базис план может быть улучшен, то есть может быть найден другой базисный план с большим значением целевой ф-ции.

3.Построение нового базисного плана

Каждый последовательный базисный план отличается только одной базисной переменной, то есть одна переменная исключается из базисной, а на ее место включается другая.

Процесс перехода от одного базиса к другому основывается на алгоритме Гауса – Жорданна.

33. м- метод. Решение задач с искусственным базисом.

Если среди ограничений равенств задач ЛП после попытки привести ее к канонической форме остались такие, в которых отсутствует базисная переменная, то начальный этап СМ невозможен.

Тогда используют методы искусственного базиса.

М – метод.

В ограничениях, не содержащих базисных переменных, добавляем со знаком + не отрицательную искусственную переменную. При этом в целевой фукции добавляются со знаком – сумму искусственных переменных, умноженное на сколько угодно большое положительное число М.

Это задача называется М-задача.

Теорема о связи решения М задачи м ЛП:

1. Если в оптимальном решении м задачи все искусственные переменные равны 0 , то соответствующее значение основных переменных составляют оптим план исходной задачи.

2. Если в оптим плане м задачи хотя бы одна искусственная переменная отличная от 0, то исходная задача не имеет решения, так как у нее нет вообще планов.

3. Если м задача неразрешима, то и исходная не разрешима.

При решении м задачи С-методом, СТ для целевой функции отводится 2 индексной строки: в 1ой записываются коэф-ты основных переменных, во 2ой перед искусственными. Заметим, что так как в м задаче целевая функция всегда содержит базисные переменные, то первая симплекс таблица всегда заполняется по правилу цен.

До тех пор пока м строка присутствует в СТ оптимальность плана проверяется по ней, при этом ф строка рассматривается как просто строка.

По м строке же определяются переменная, включающая в базисную, так продолжается до тех пор пока все искусственные переменные не будут исключены из базиса.

По теореме, если все элементы м строки = 0 то исходная задача имеет план.