Вопрос 24. Математическое ожидание и его свойства.

Математическое ожидание

Не всегда для характеристики случайной величины нужно указывать закон ее распределения. Иногда достаточно некоторых усредненных величин.

Математическое ожидание – это среднее значение случайной величины среди всех возможных.

1. Математическое ожидание для дискретных величин:

2. Математическое ожидание для непрерывных величин:

где x – это плотность распределения

Свойства математического ожидания:

1. M(C) = C, где C – константа

2. M(

3. 

4. , где C – константа

5. Если X и Y – независимые случайные величины, то

Две величины независимы друг от друга, если вероятности значений одной из них не зависят от вероятностей значений другой.

6. Математическое ожидание отклонения величины от математического ожидания равно нулю: M(X-M(X)) = 0

Вопрос 25. Дисперсия и ее свойства.

Дисперсия случайной величины

Дисперсия – это математическое ожидание квадрата отклонения случайной величины от математического ожидания.

1. Дисперсия для дискретной величины:

где a – это математическое ожидание

2. Дисперсия для непрерывной величины:

Свойства дисперсии

1. D(C) = C, где C – константа

2. D(

3. 

4. 

Для справки!

Среднее квадратическое отклонение – величина

Вопрос 26. Биномиальный закон распределения и закон распределения Пуассона.

Биномиальный закон распределения

Дискретная величина имеет данный закон с параметрами n и p, если принимает значения 0, 1, 2, 3 … n при учете:

=

где q = 1-p

Биномиальный закон часто применяется при статистике качества продукции.

Ряд распределения данной случайной величины:

X	0	1	…	m	…	n
			…		…

Теорема:

Если дискретная случайная величина имеет биномиальный закон распределения, то математическое ожидание M(X) = np, дисперсия D(X) = npq.

Закон распределения Пуассона

Дискретная случайная величина имеет закон Пуассона с параметром , если она принимает значения 1, 2 … m … (счетное, но бесконечное) при учете

Теорема:

Если дискретная случайная величина имеет закон распределения Пуассона, то M(X) = D(X) =

Вопрос 27. Равномерный и показательный законы распределения.

Равномерный (прямоугольный) закон распределения

Непрерывная случайная величина имеет равномерный закон распределения на [a; b], если ее плотность постоянна на данном отрезке и равна нулю вне его.

Теорема:

Если непрерывная случайная величина имеет равномерный закон распределения на отрезке [a; b], то:

В таком случае:

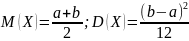
Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина имеет показательный закон распределения с параметром , если ее плотность распределения вероятности f(x):

Теорема:

Если случайная величина имеет показательный закон, то функция F(x):

В таком случае:

Вопрос 28. Нормальный закон распределения.

Непрерывная случайная величина имеет нормальный закон распределения с параметром , если плотность распределения

где a – это математическое ожидание, а – это дисперсия

Теорема:

Если случайная величина имеет нормальный закон, то M(X)=a, D(X)= (математическое ожидание равно математическому ожиданию, дисперсия равна дисперсии)

Данная кривая – график плотности, кривая Гаусса, a – ось симметрии функции.

1) Зафиксируем G и будем менять положение оси симметрии:

По графику функции a1 < a2 < a3

2) Теперь зафиксируем a и будем менять положение G.

Пусть G1<G2<G3

Таким образом, чем больше G, тем ниже график.

Свойства случайной величины, имеющей нормальный закон распределения

1. Вероятность величины попасть в интервал :

где

2. Вероятность того, что отклонение случайной величины, имеющей нормальный закон распределения, от ее математического отклонения, не превысит некоторую величину :

где