Пример расчета

На рис. 2.1 приведена схема электрической цепи, содержащей источники ЭДС и тока, численные значения параметров приведены в табл. 2.2.

Таблица 2.2

Em1

ψE

Jm2

ψJ

R1

L1

C1

R2

L2

C2

R3

L3

C3

В

град

A

град

Ом

мГн

мкФ

Ом

мГн

мкФ

Ом

мГн

мкФ

25

0

15

30

2

0,6

∞

12

4,5

60

18

3

12

f
Гц	Ом	См	мГн
500	5	0,25	1,27

1. Предварительно выполним эквивалентное преобразование схемы:

заменим источник тока А,

на эквивалентный источник ЭДС ( ) с ЭДС В и внутренним сопротивлением Ом.

Получили два последовательно соединенных источника ЭДС:

и ( В, В), заменим их одним

эквивалентным источником ЭДС ( ).

В,

Ом, Ом.

2. Рассчитаем эквивалентное сопротивление приемника

, Ом,

Ом,

Ом, Ом,

Ом.

3. Рассчитаем полное сопротивление цепи

Ом.

Результаты расчетов сведены в табл. 2.3.

Таблица 2.3

Сопротивление	В алгебраической форме	В показательной форме
	Ом
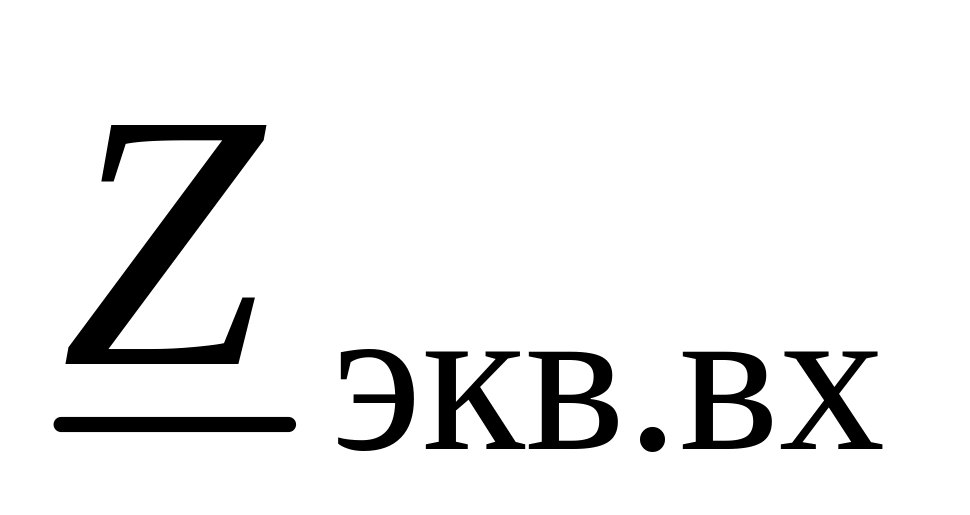
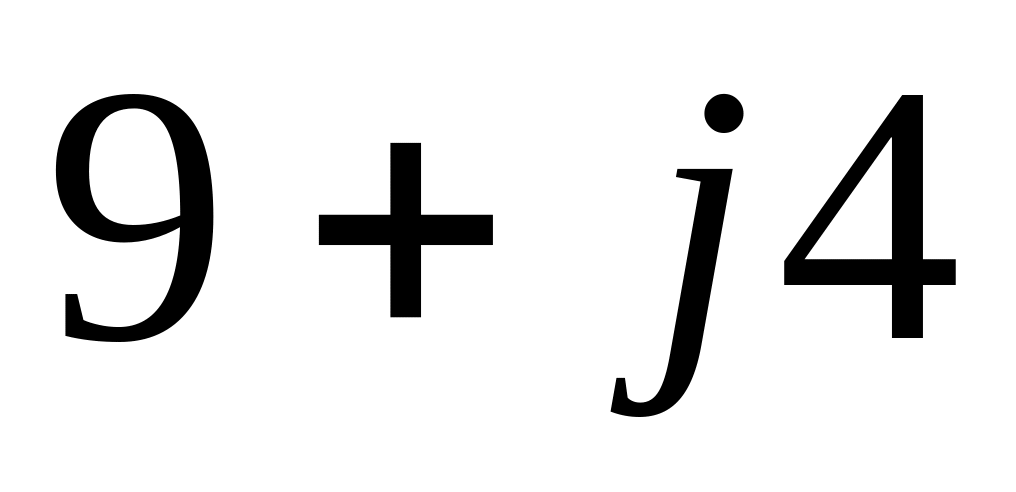
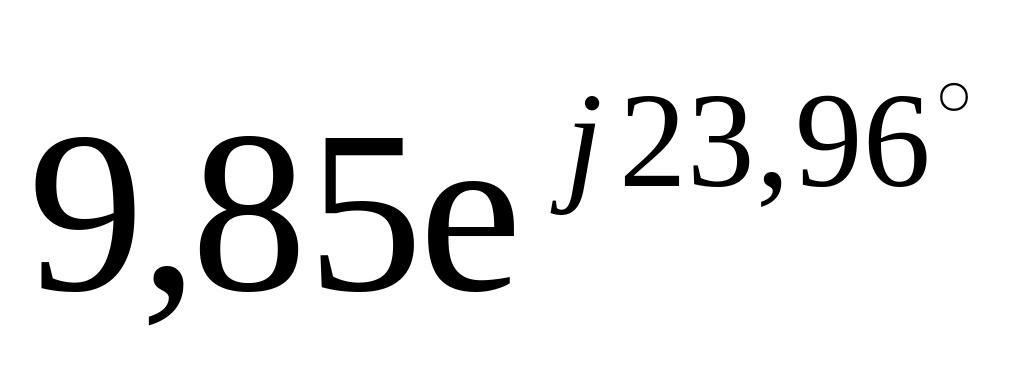
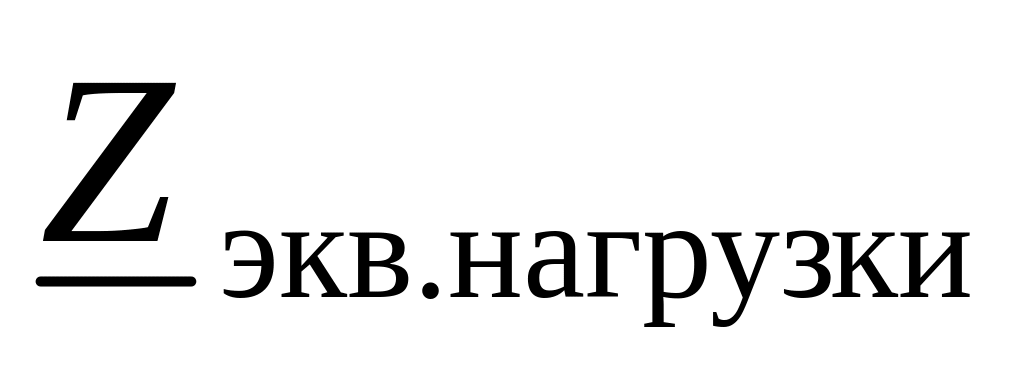
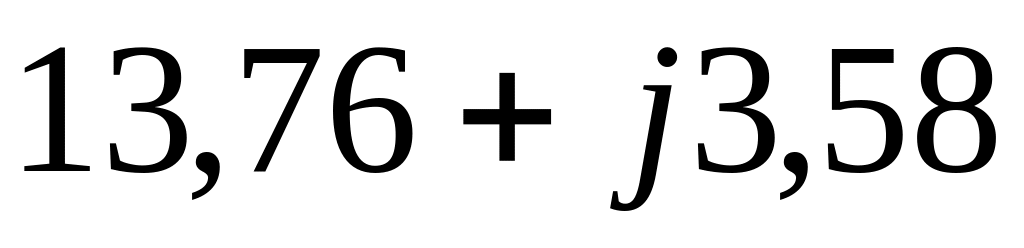
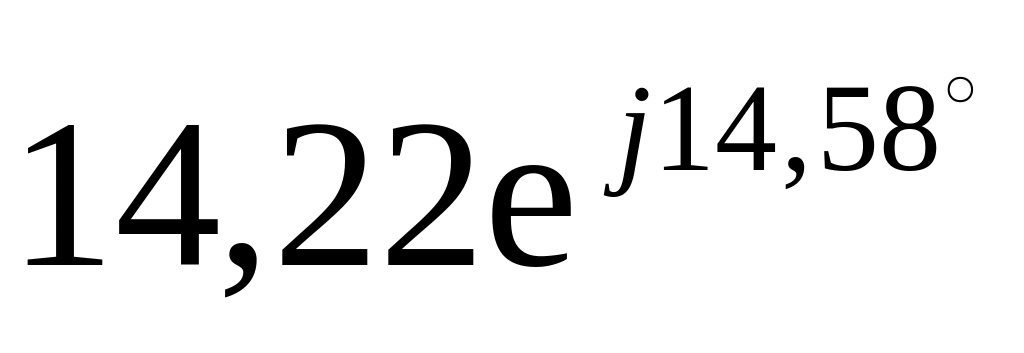
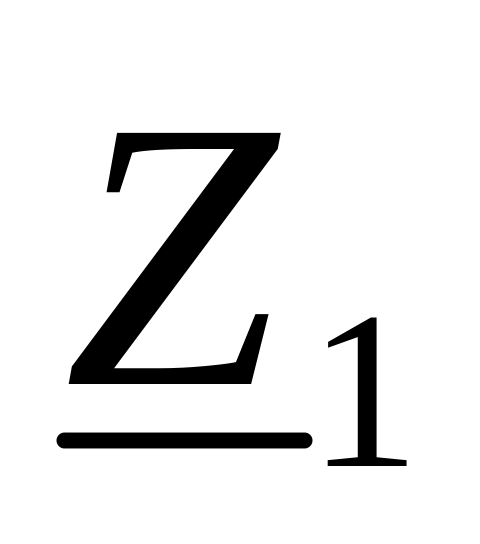
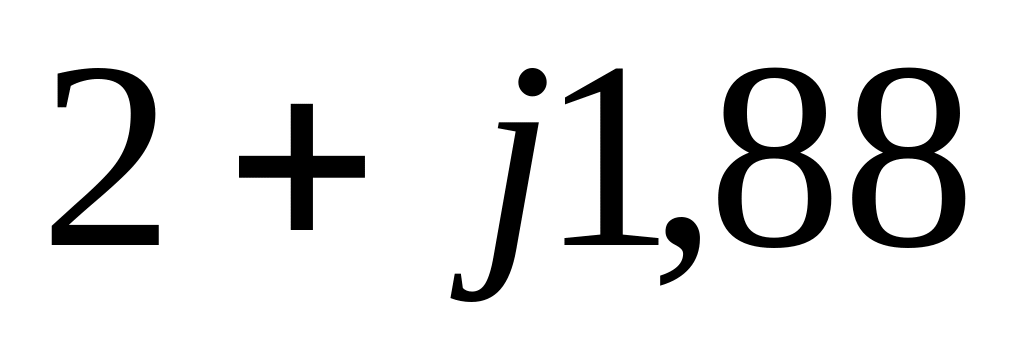
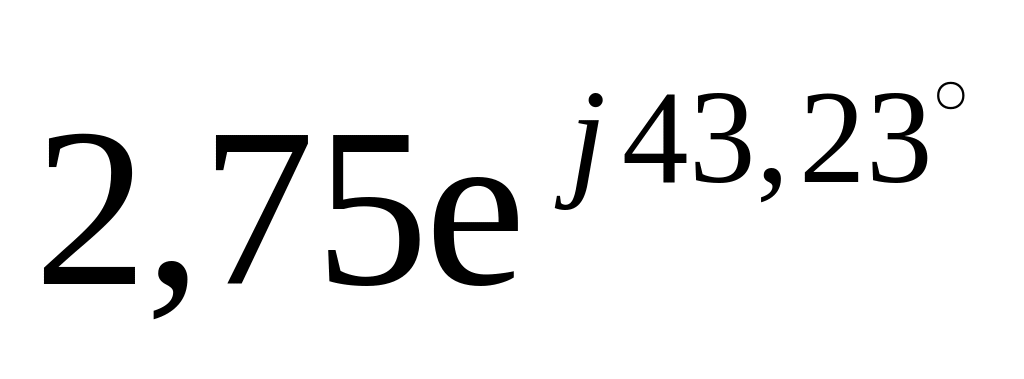
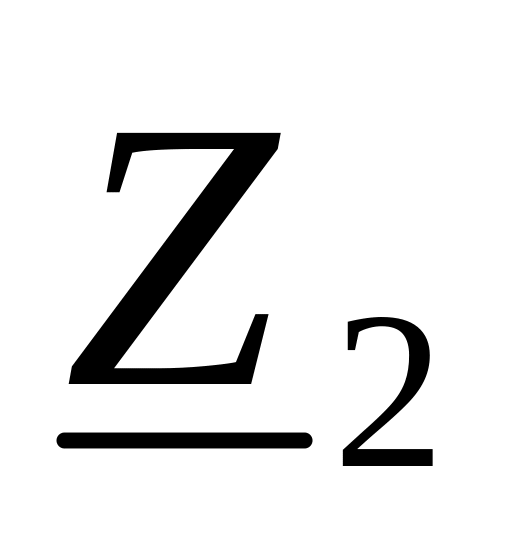
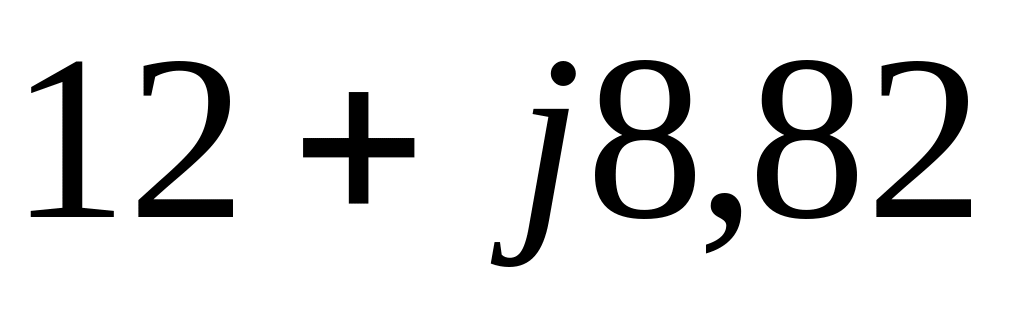
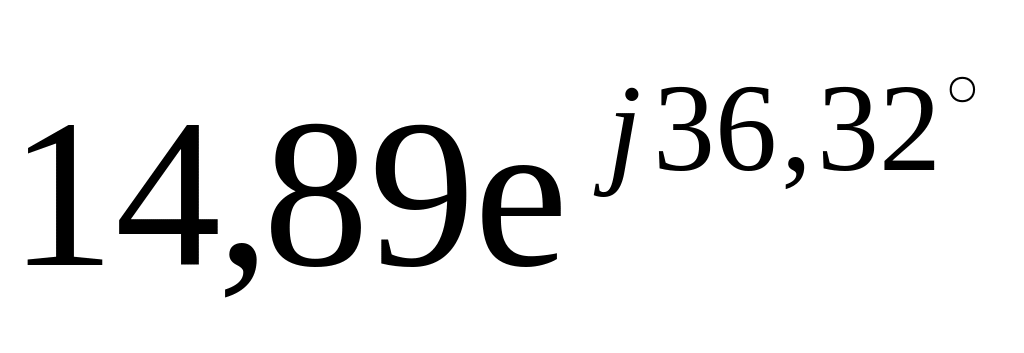
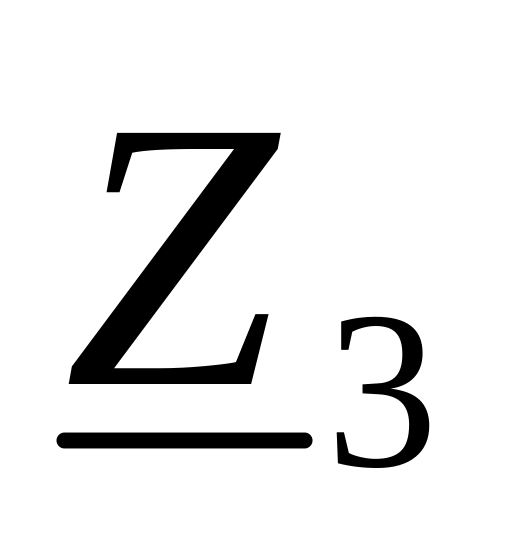
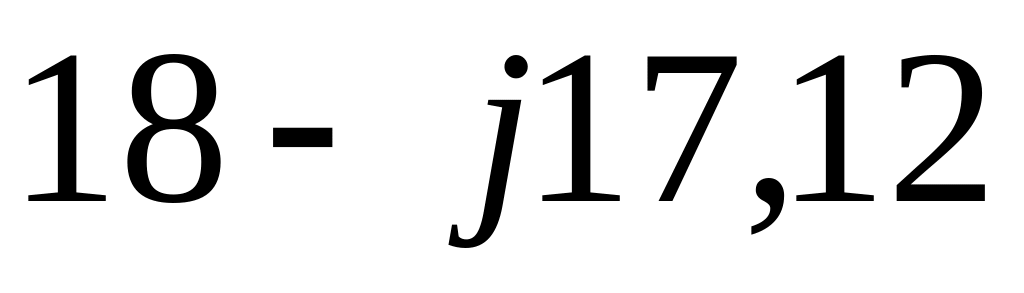
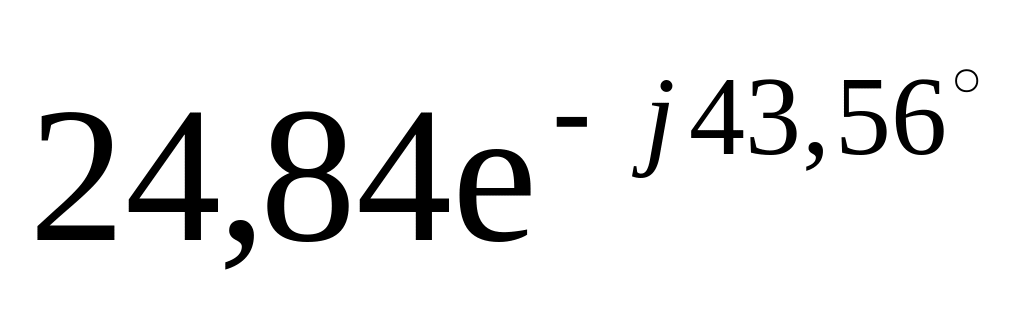
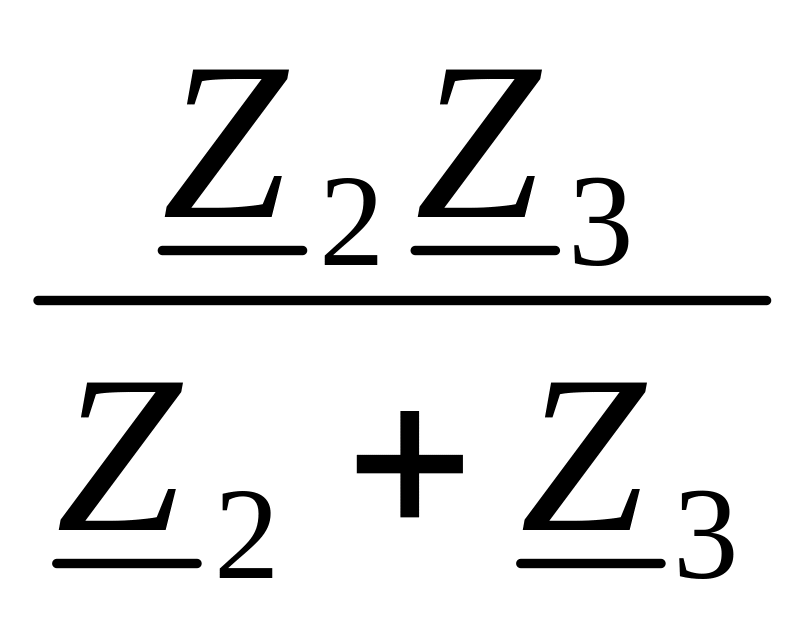
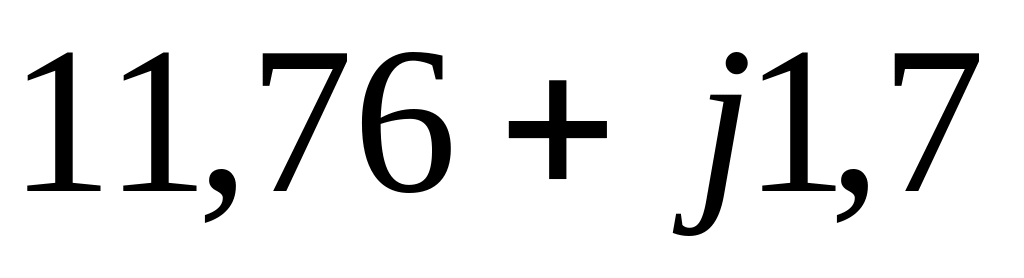
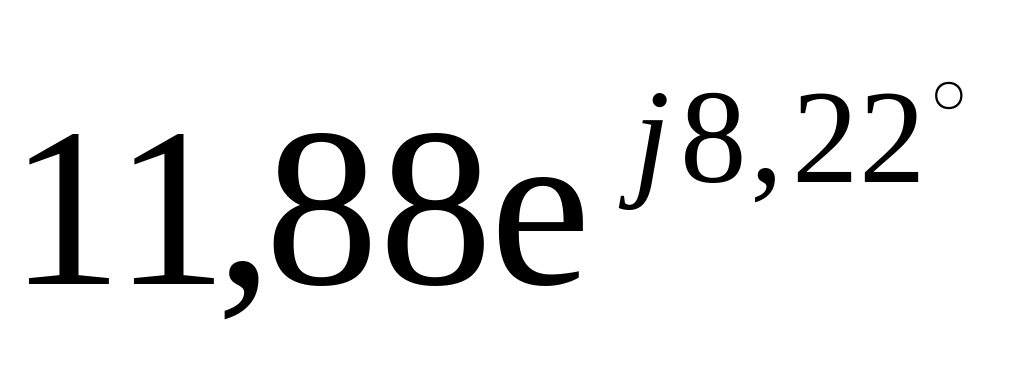
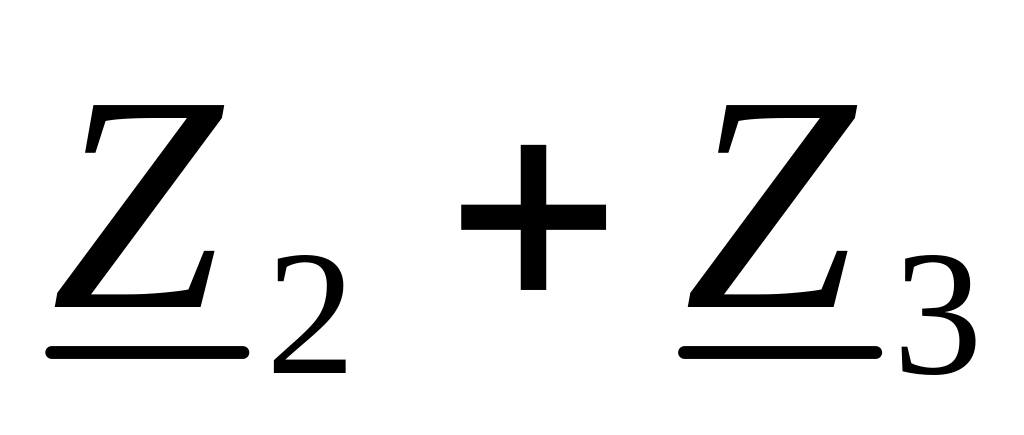
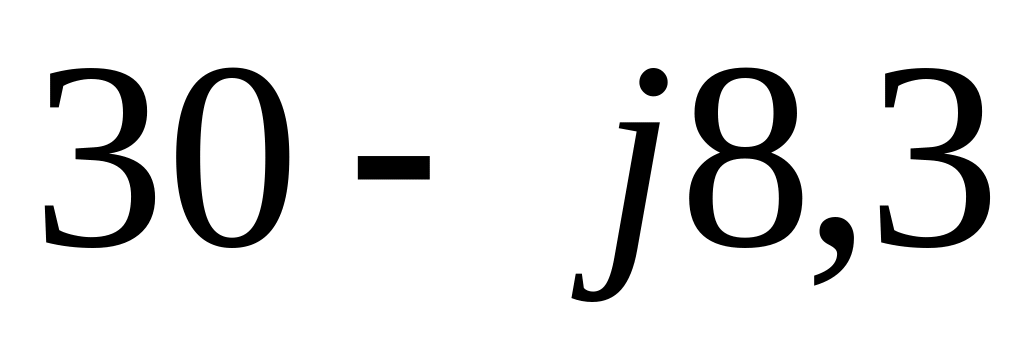
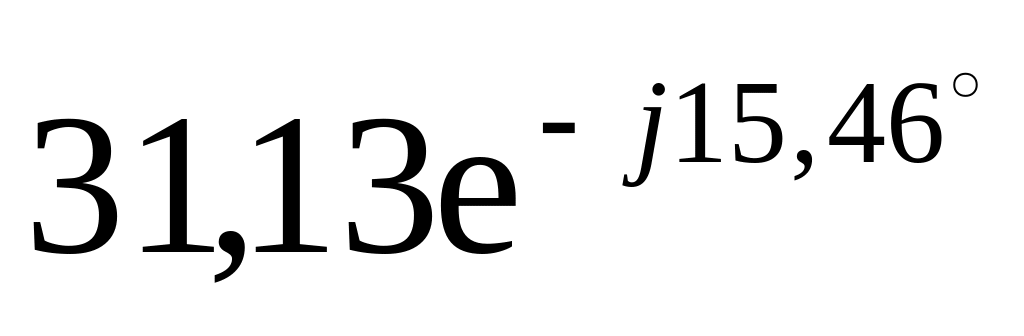
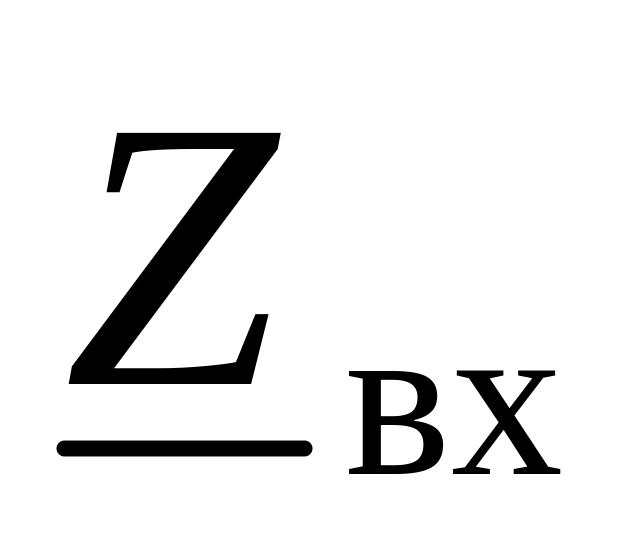
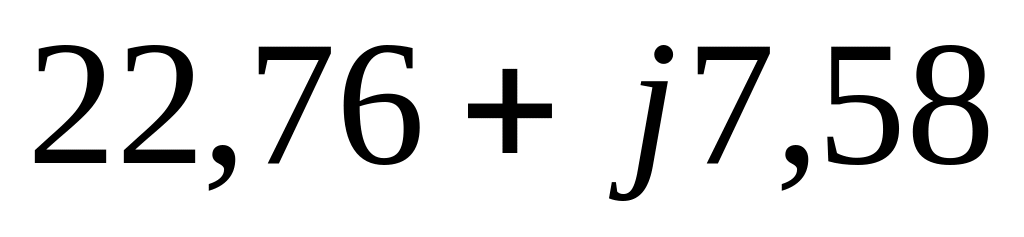
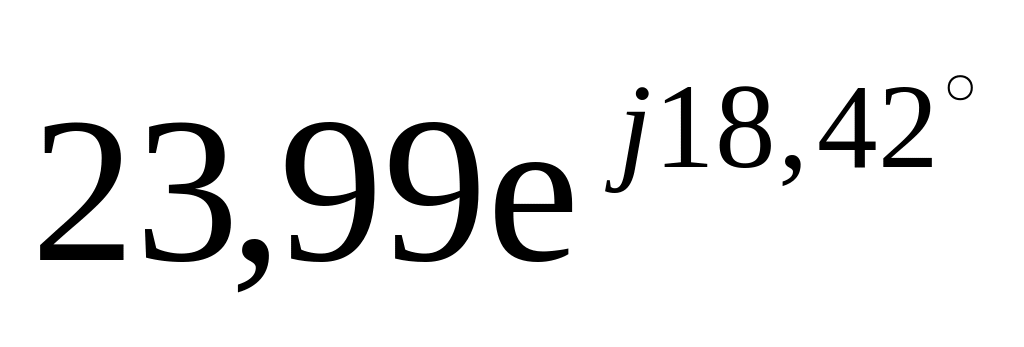
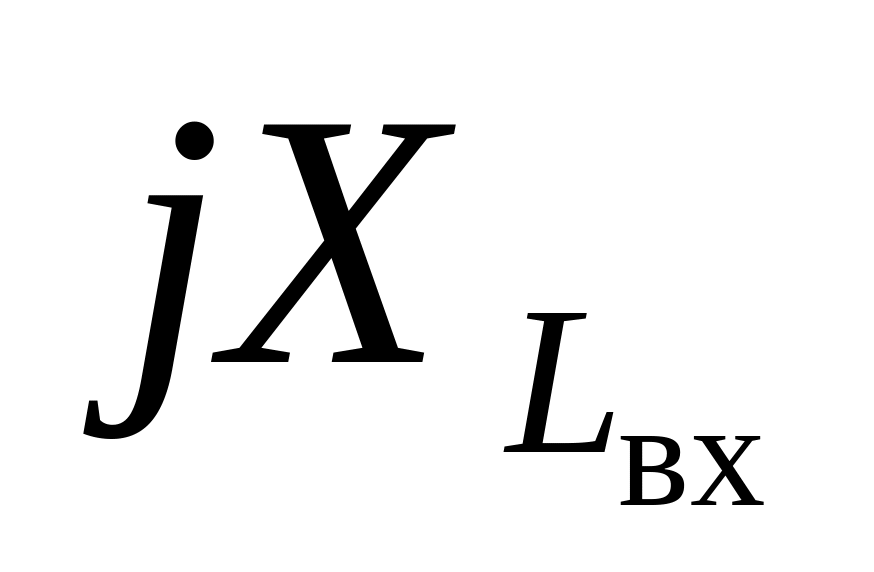
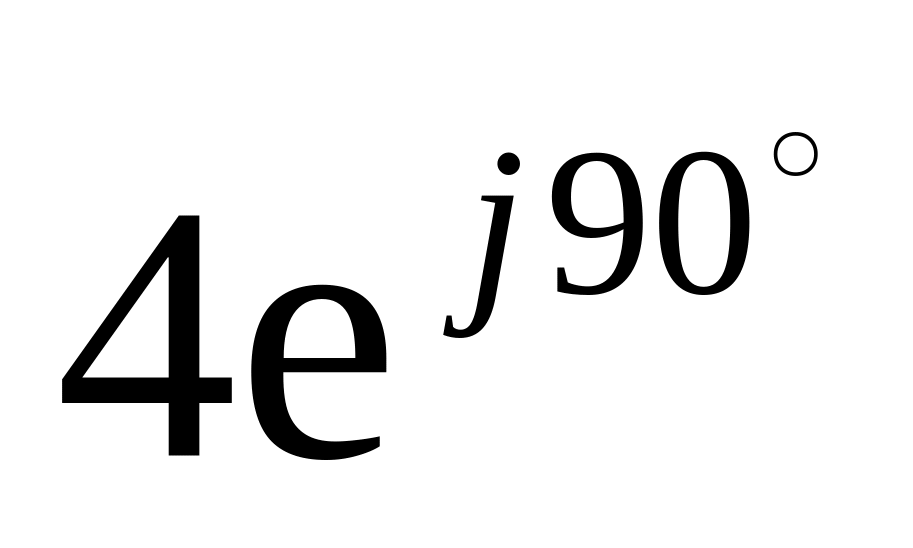
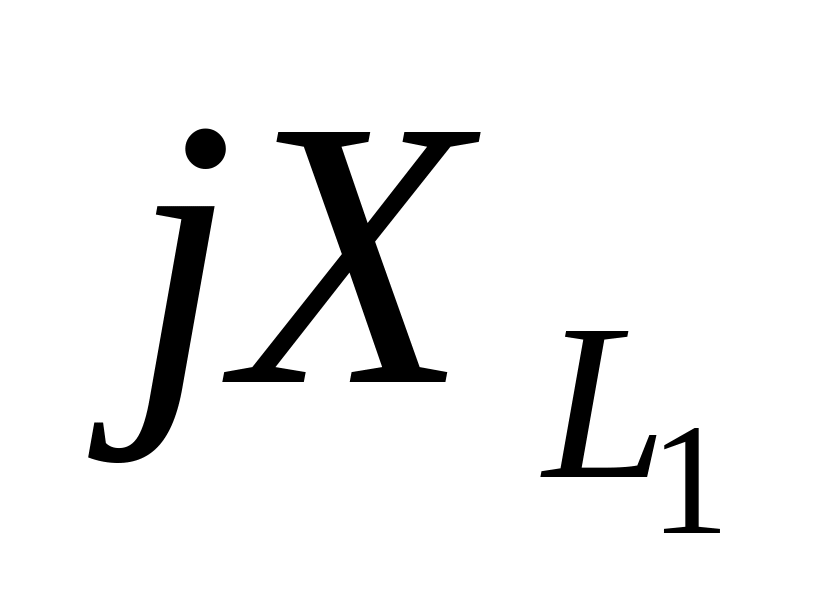
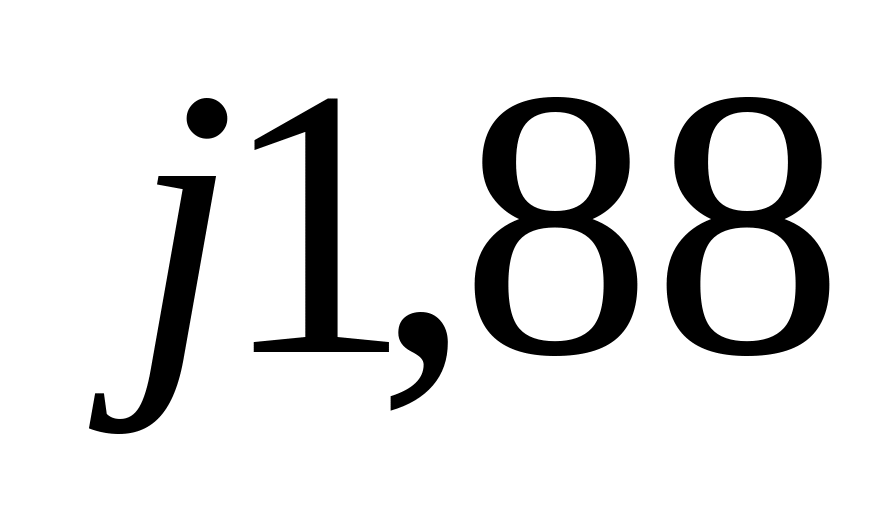
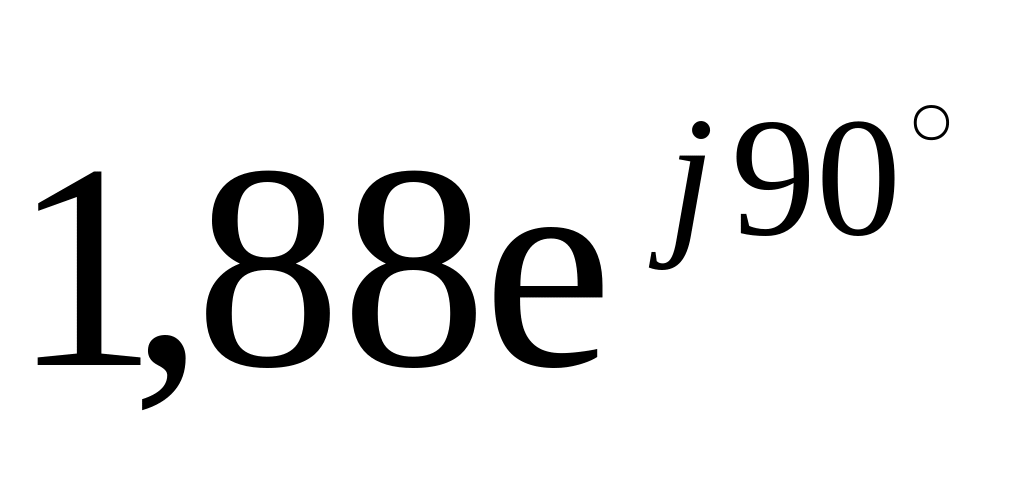
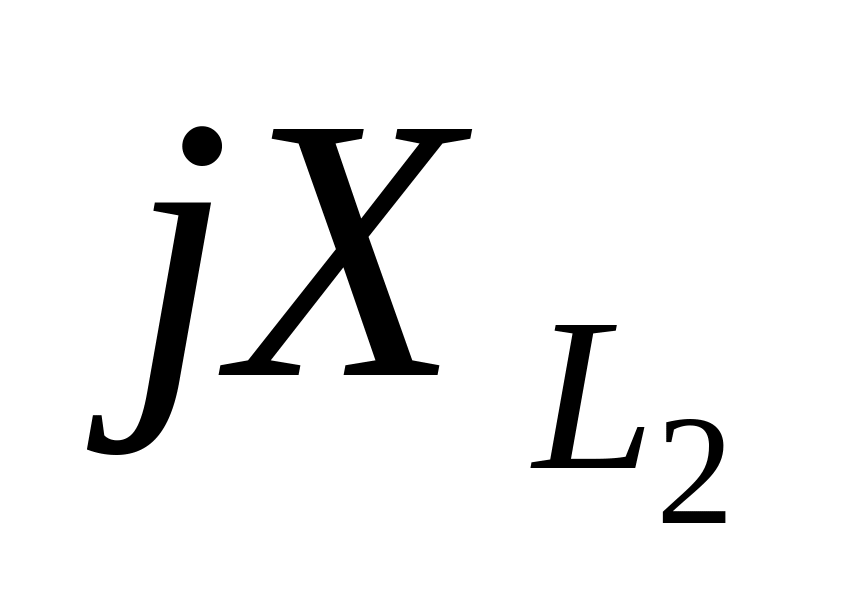
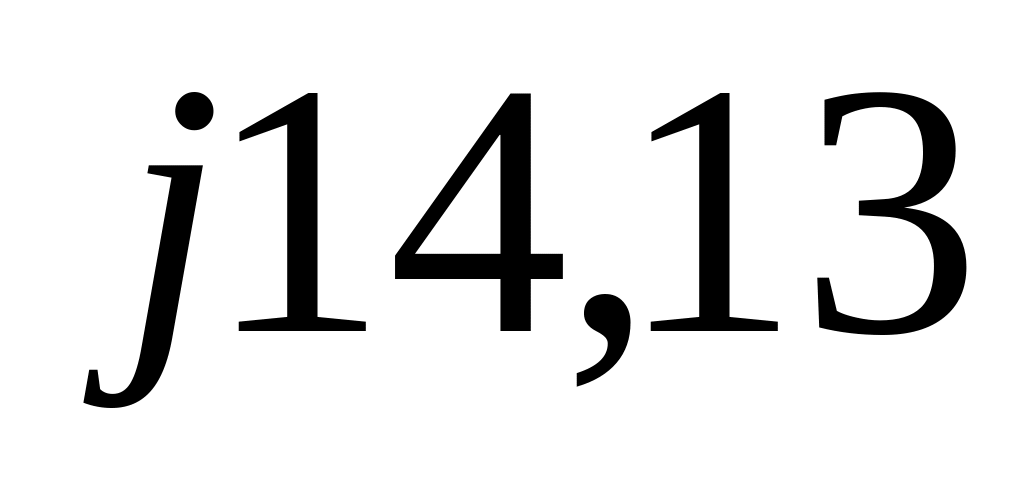
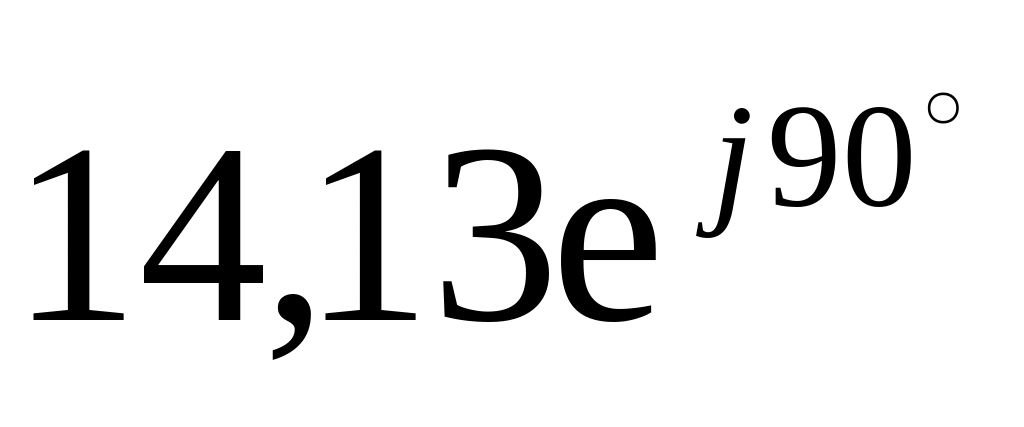
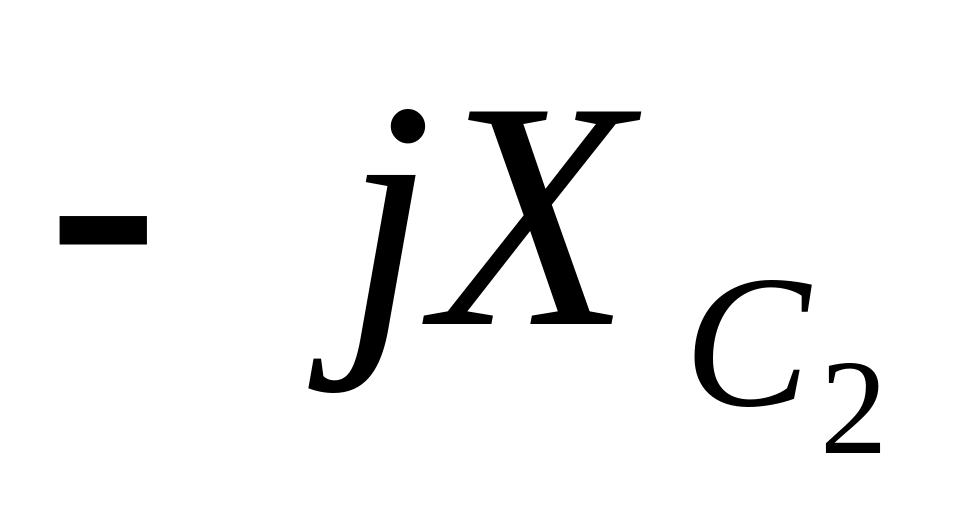
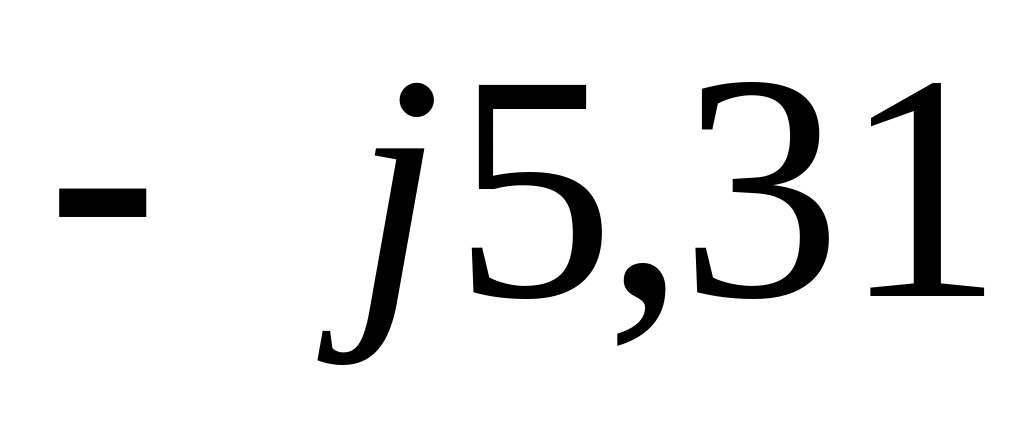
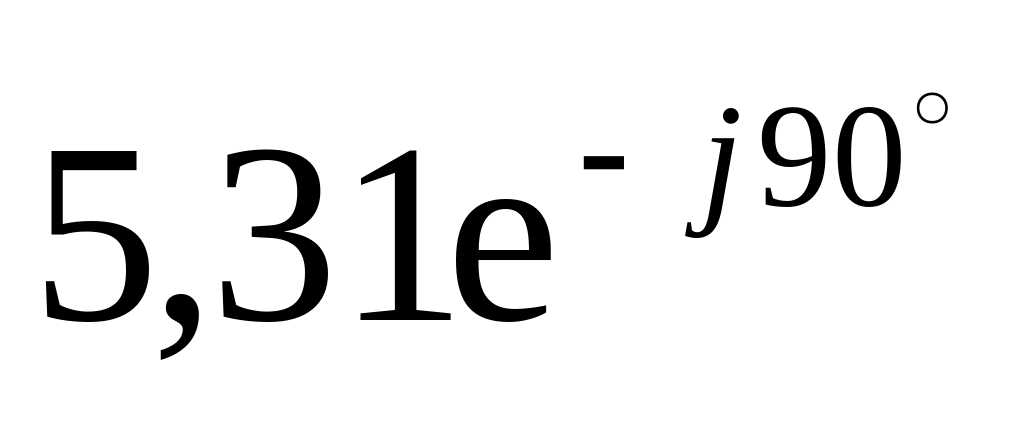
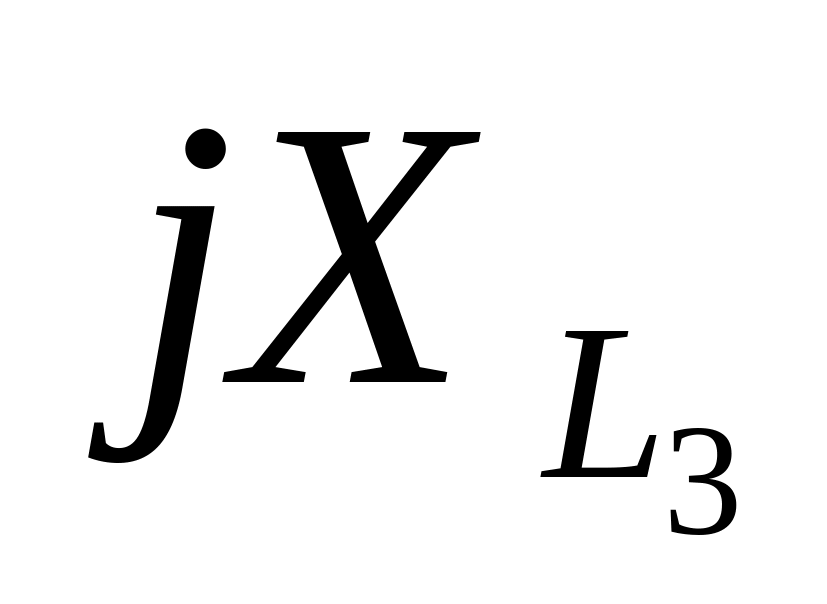
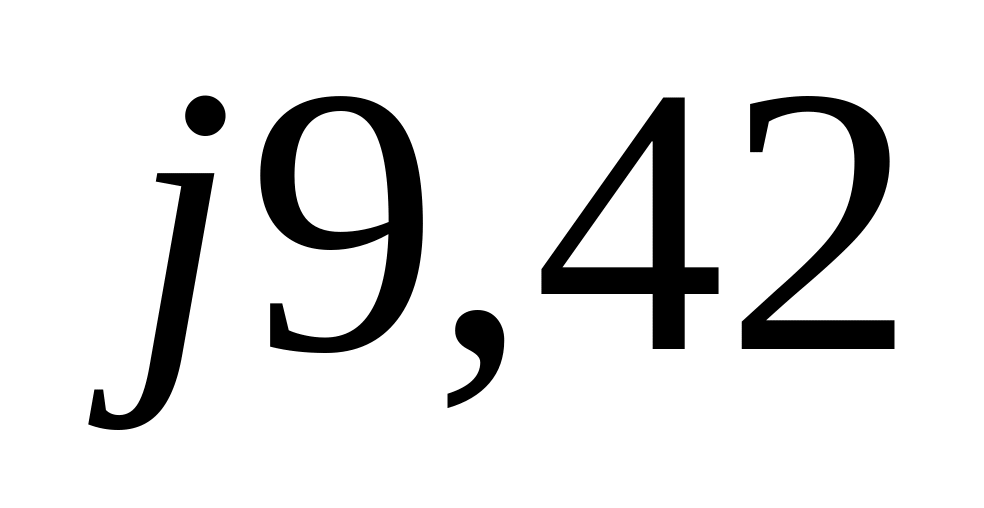
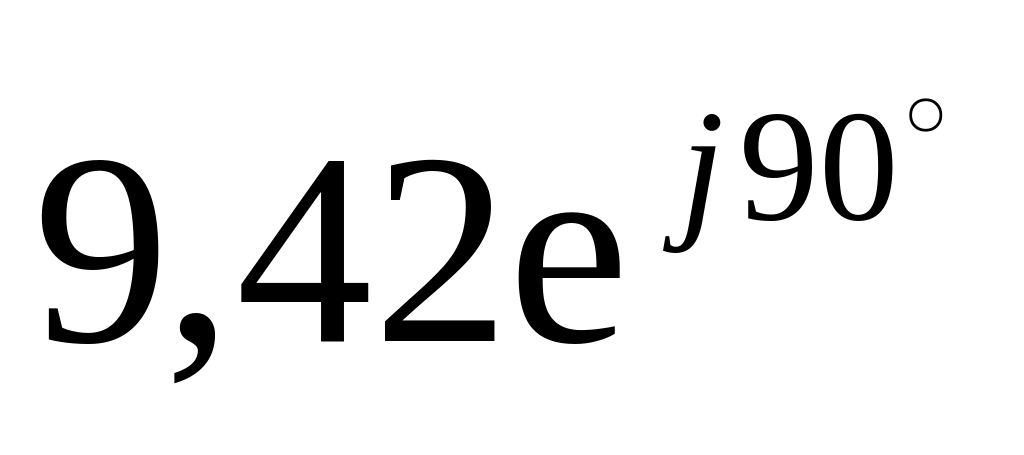
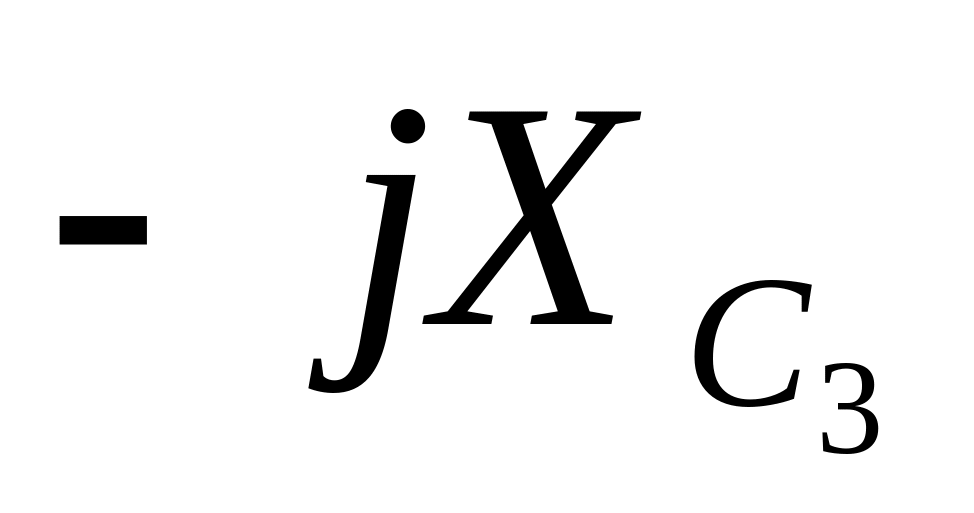
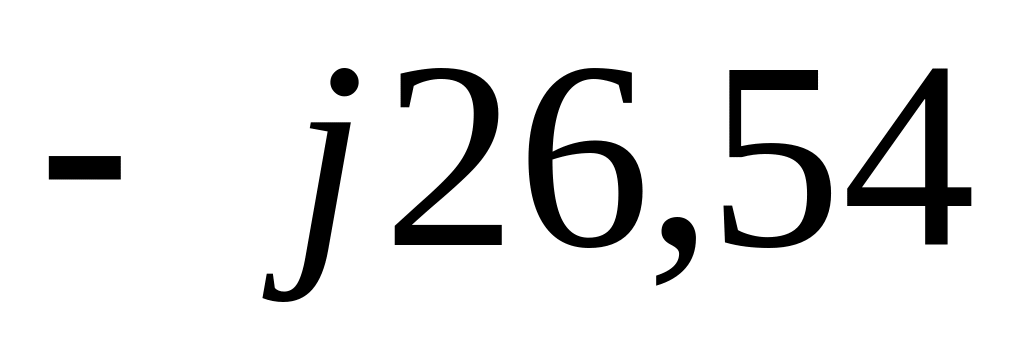
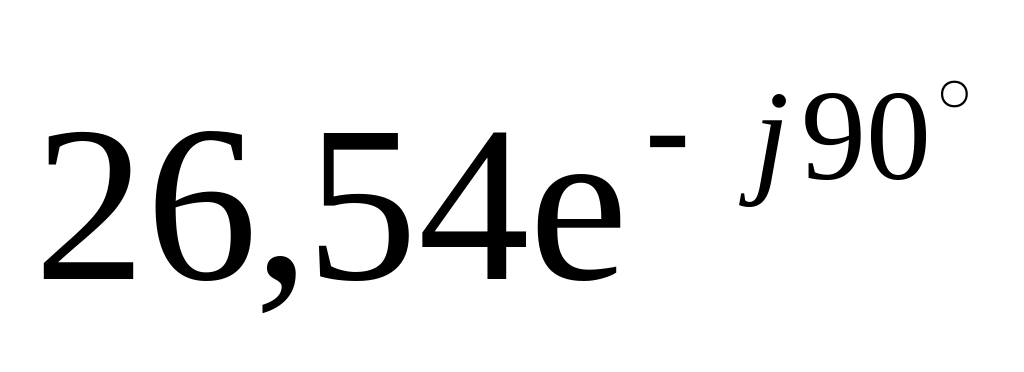
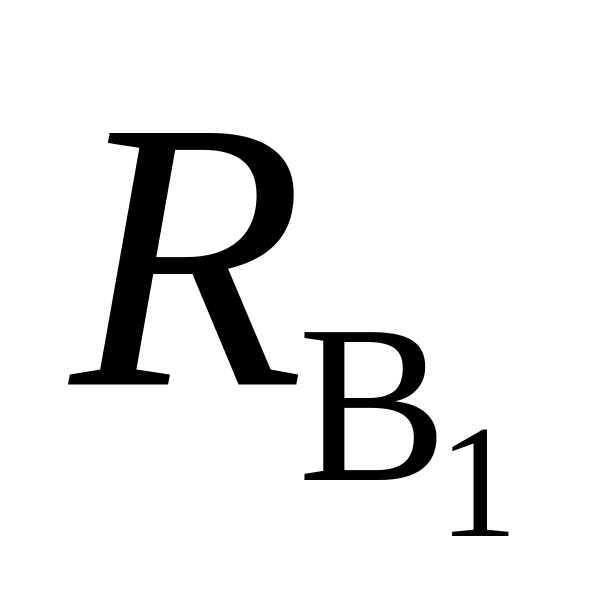
	5	5
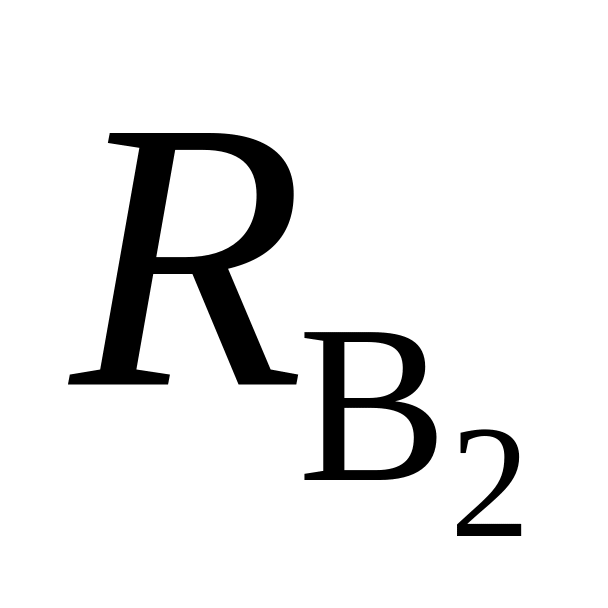
	4	4
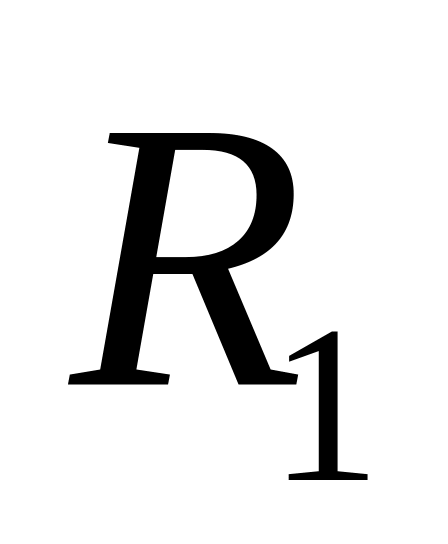
	2	2
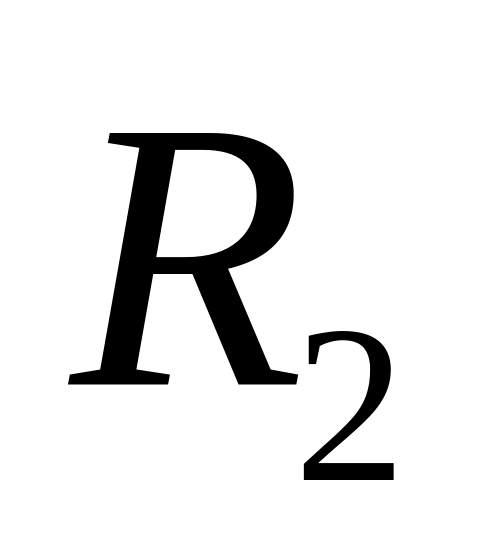
	12	12
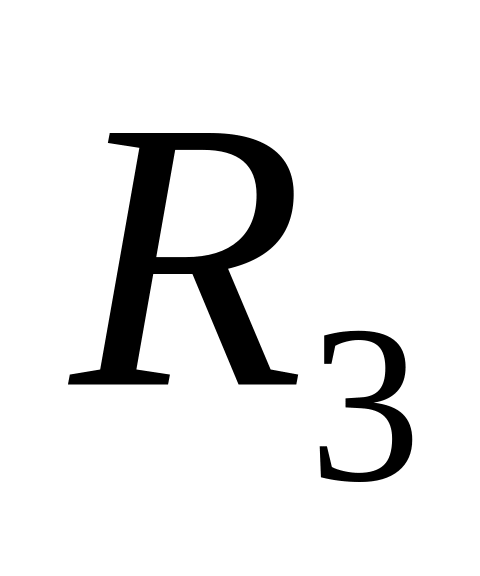
	18	18
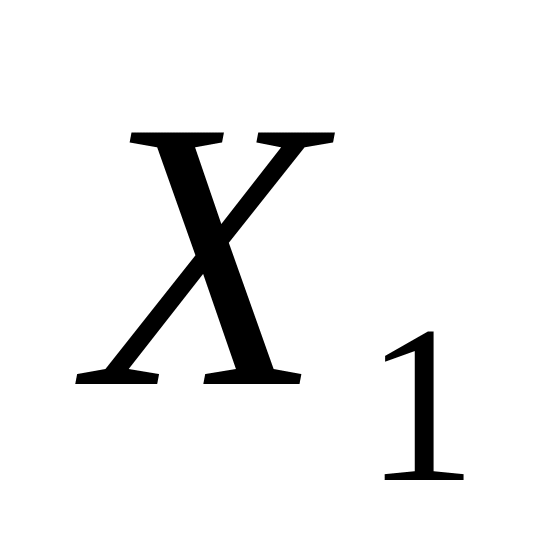
	1,88	1,88
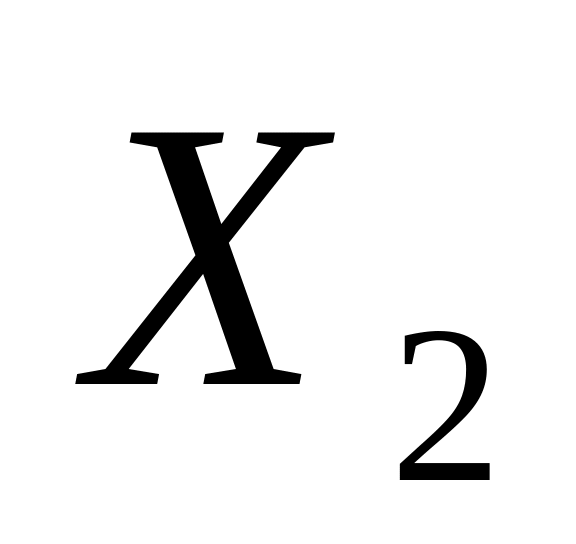
	8,82	8,82
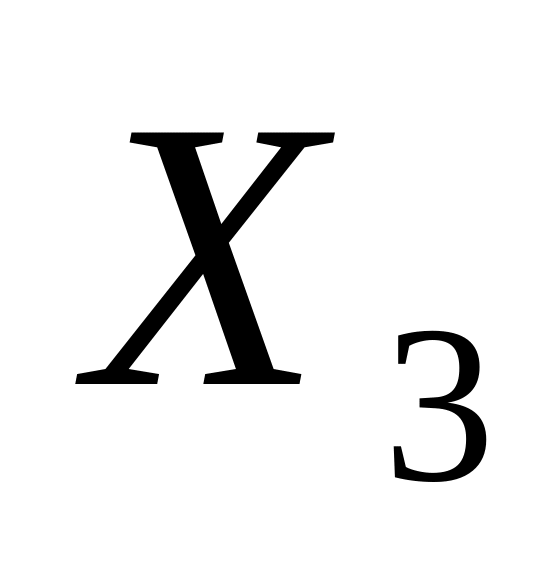
	-17,12	-17,12

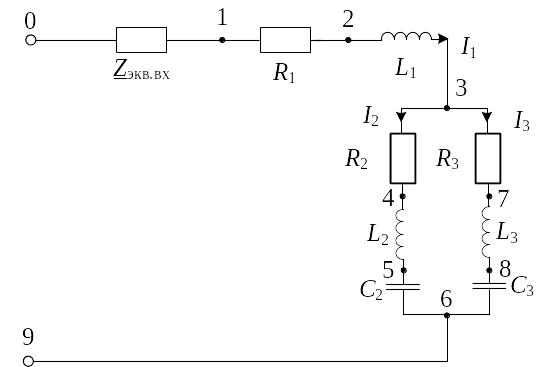
4. Рассчитаем токи в ветвях приемника

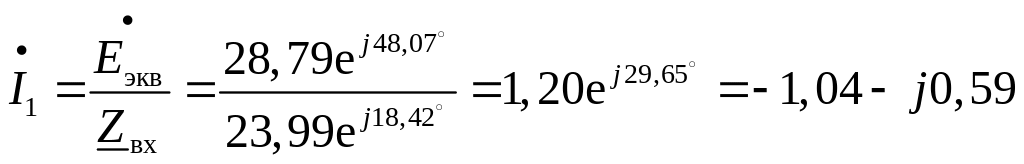А,

А,

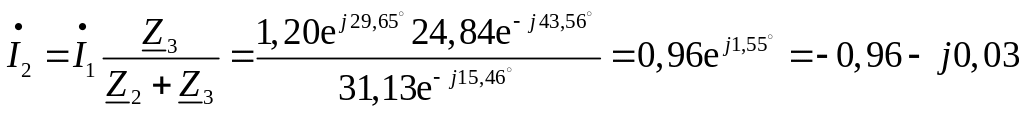А.

5. Рассчитаем напряжения на элементах цепи (рис. 2.5) 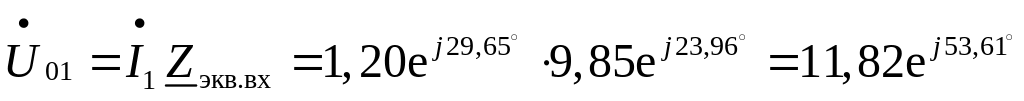В, В,

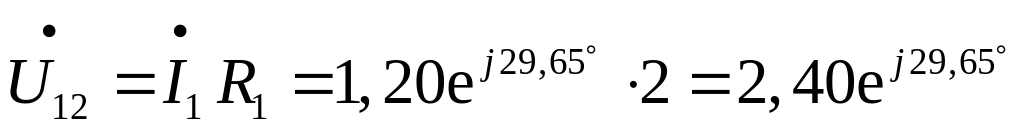В, В,

В, , В, В В, В.

Рис. 2.5

По полученным величинам строим векторную диаграмму токов (согласно первому закону Кирхгофа) и топографическую диаграмму напряжений (согласно второму закону Кирхгофа, рис. 2.6).

Внимание. Векторы напряжения и тока на активном сопротивлении совпадают по направлению; вектор напряжения на индуктивности опережает вектор тока на угол 90°; вектор напряжения на емкости отстает от вектора тока на угол 90°.

6. Определим показания приборов

• амперметр показывает действующее значение тока

A;

• вольтметр показывает действующее значение напряжения _.

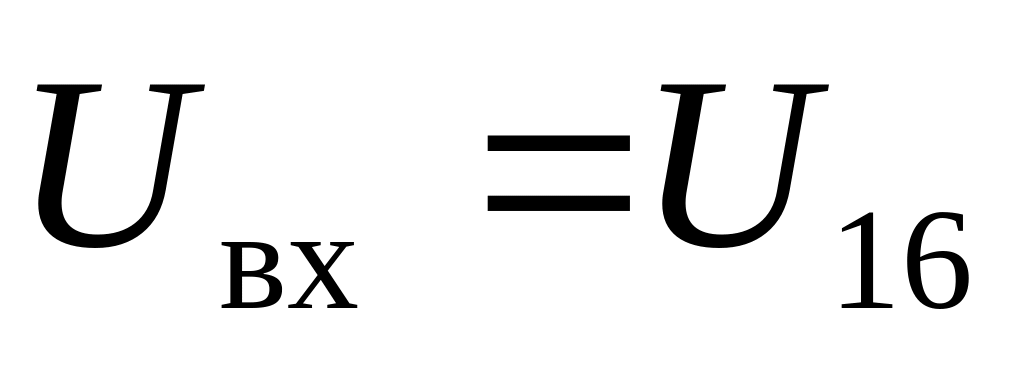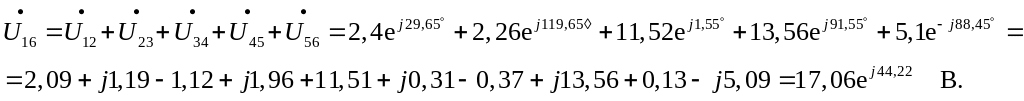
В;

• ваттметр показывает активную мощность, потребляемую приемником

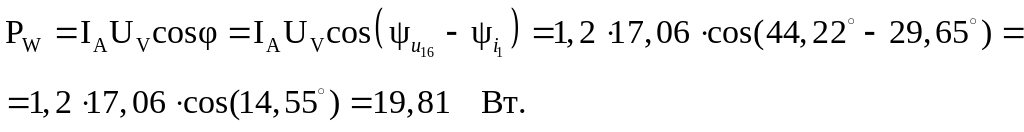
7. Рассчитаем мощности

Вт, вар,

В·А.

Коэффициент мощности равен: .

_{Внимание. В пределах погрешности расчета значение угла φ ( ) должно совпасть с фазой} .

8. Проверим баланс мощностей

Вт,

где * – знак сопряжения,

,

Вт,

вар,

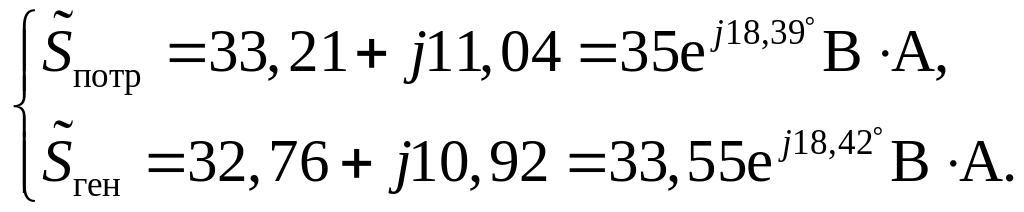
Расхождение между модулями полных мощностей равно

.

Расхождение между фазами полных мощностей равно

.

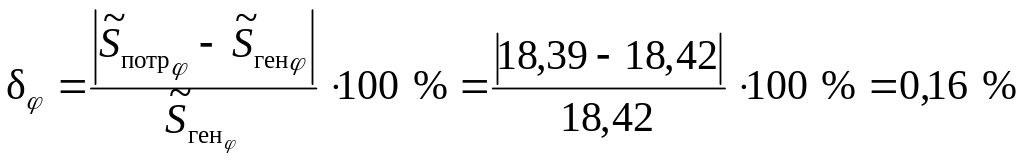9. Запишем формулы для мгновенных значений величин

,

,

,

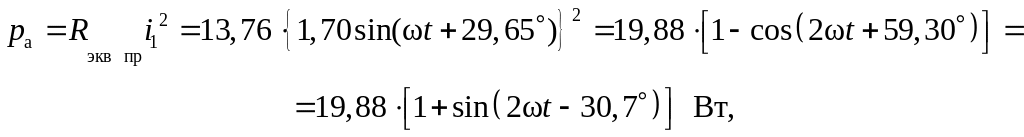
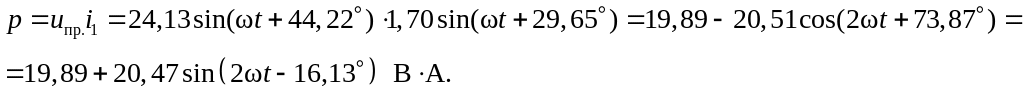
Графики величин приведены на рис. 2.7.

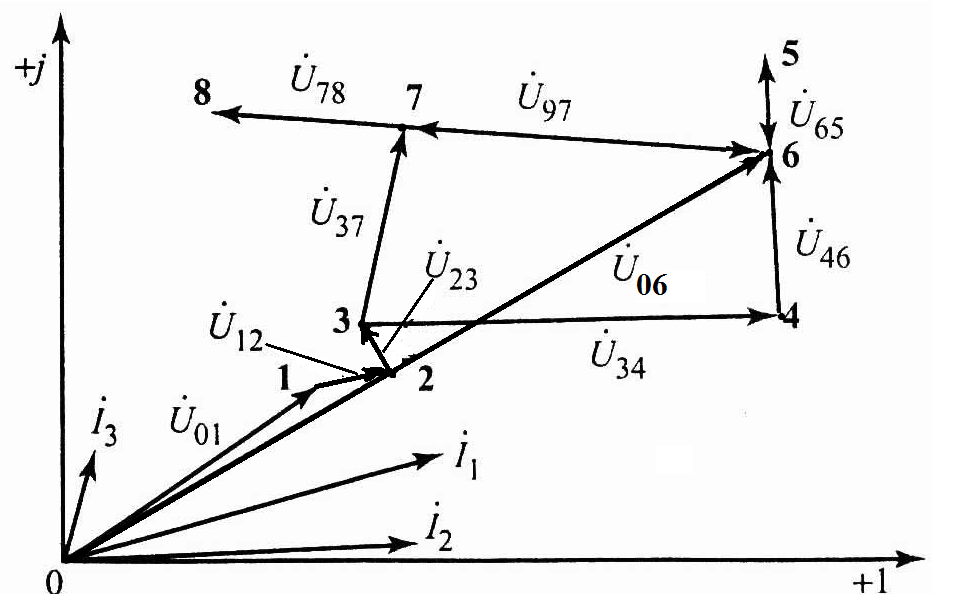
Рис. 2.6

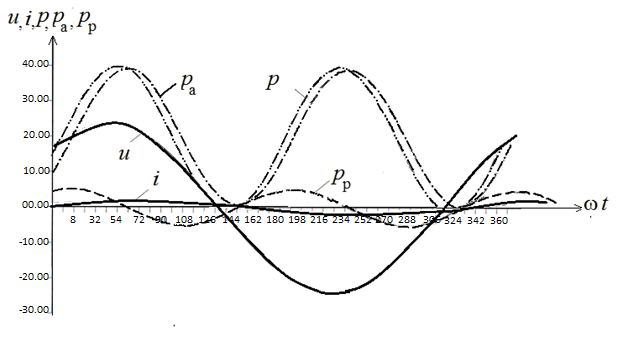
Рис. 2.7

ЗАДАНИЕ №3