§ 2. Векторна алгебра в звичайному просторі. Основні поняття і теореми [5, с. 89-91, 92-95, 97-99, 101-102; 9, с. 54-65.] Зразки розв’язування задач
Задача 1. Дано координати точок
,
,
,
,
.
Засобами векторної алгебри знайти:
кут між векторами
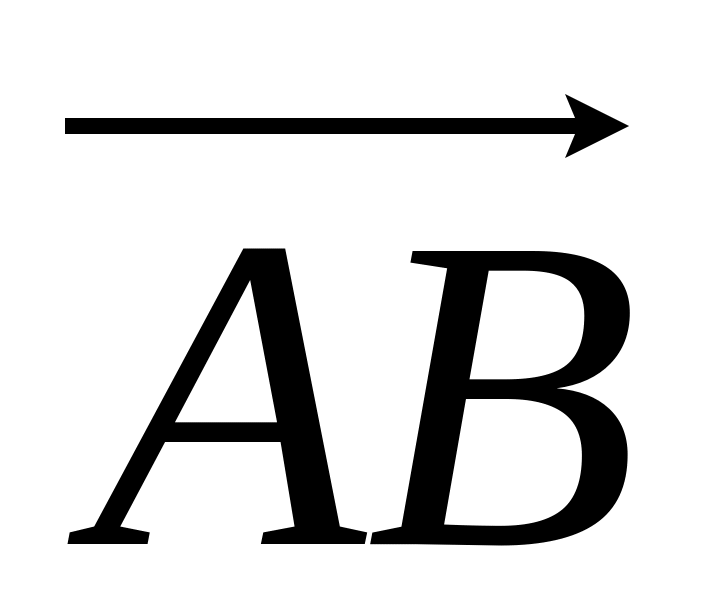і
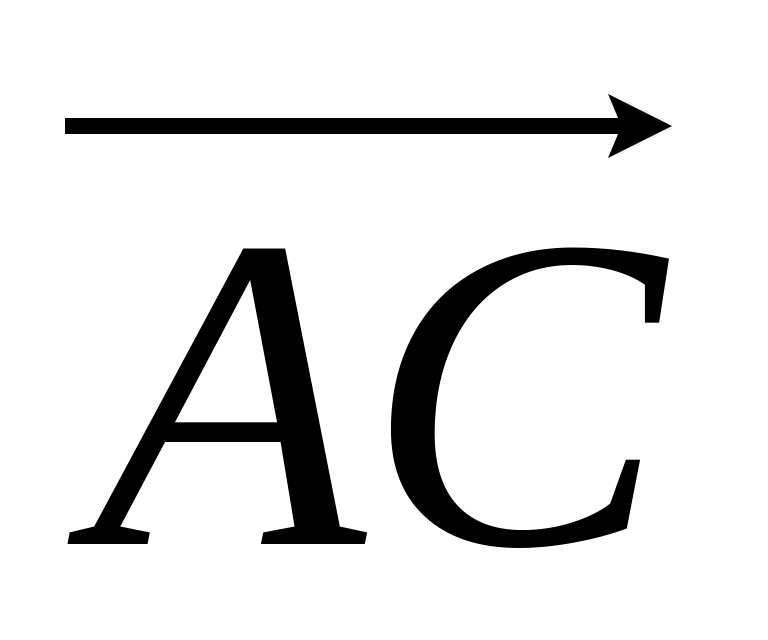;площу трикутника
;
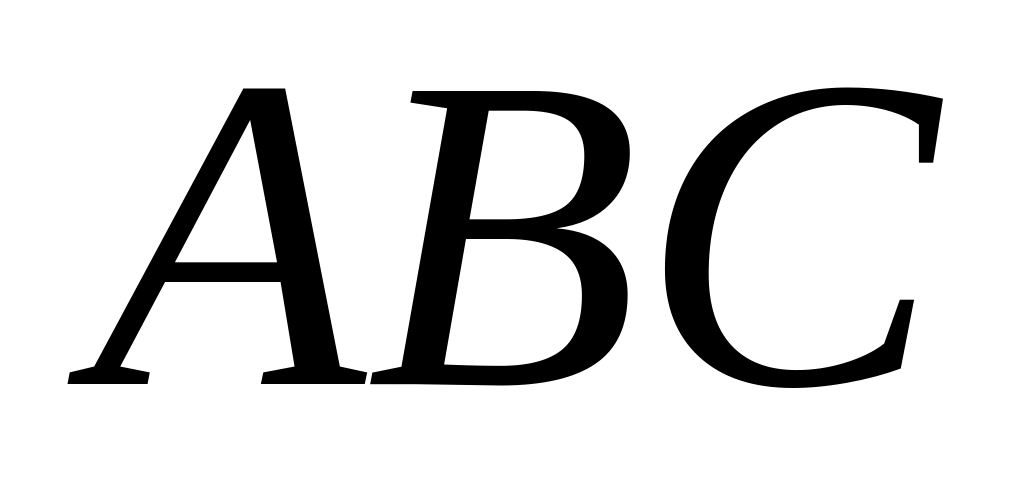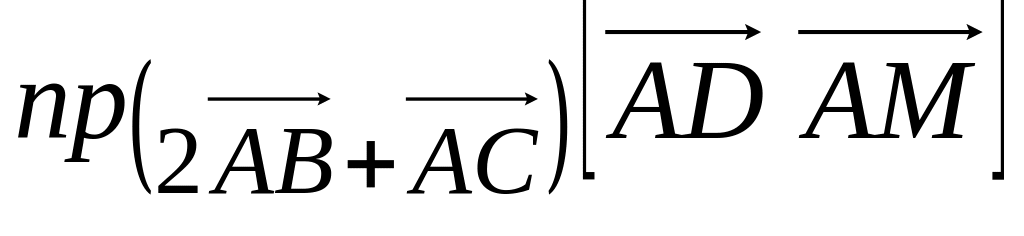;об’єм піраміди
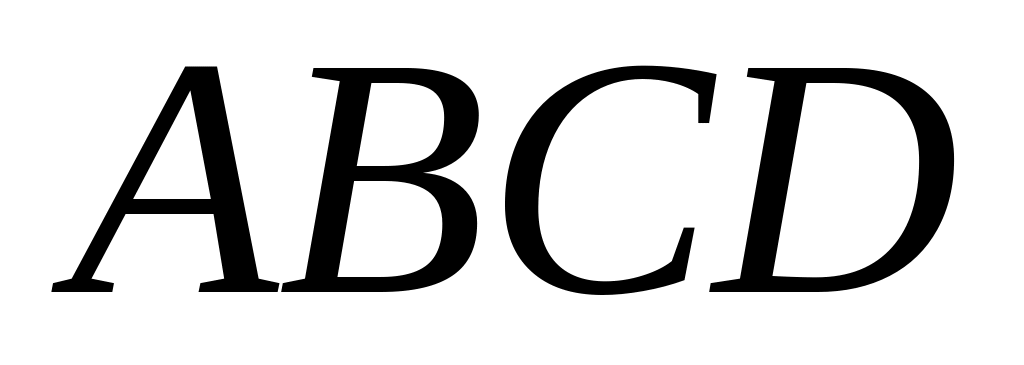;розкласти вектор
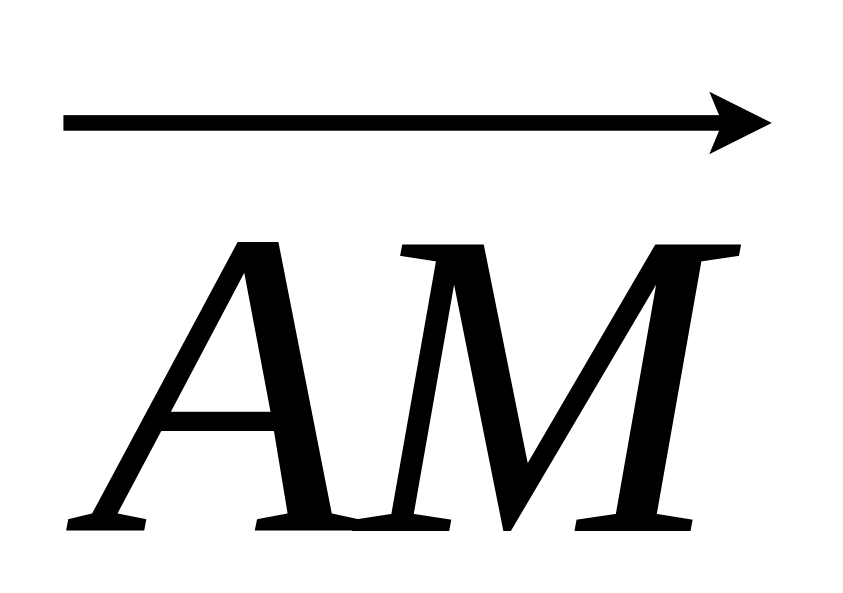за базисом із векторів
,
,
.
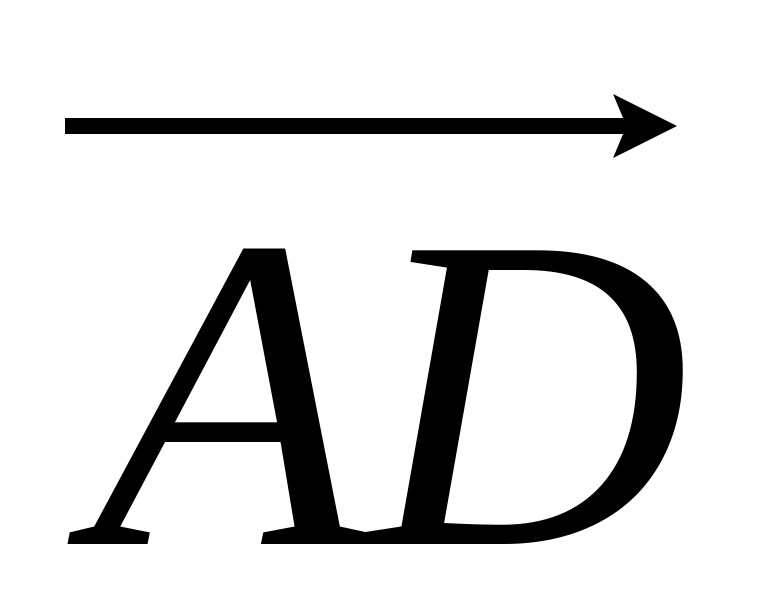Розв’язання.
Знайдемо координати векторів і . Маємо
Косинус кута між векторами і має вигляд:
Тоді
Площа трикутника дорівнює половині площі паралелограма, побудованого на векторах і , тобто половині модуля векторного добутку векторів і . Оскільки
,
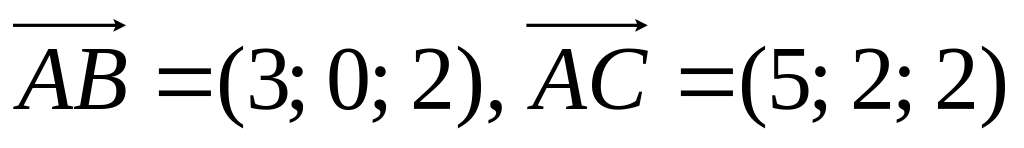то
.
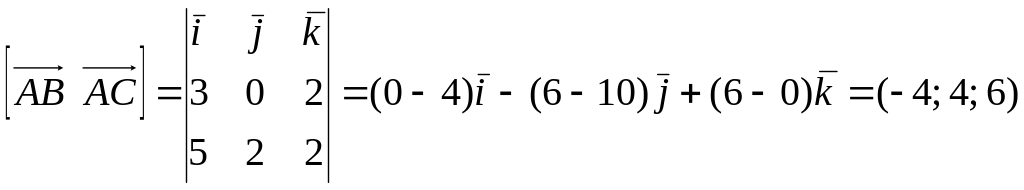Отже,
(кв. од.).
Проекція вектора
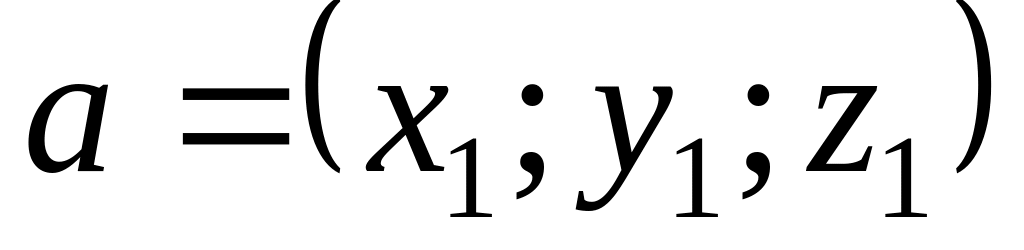на вектор
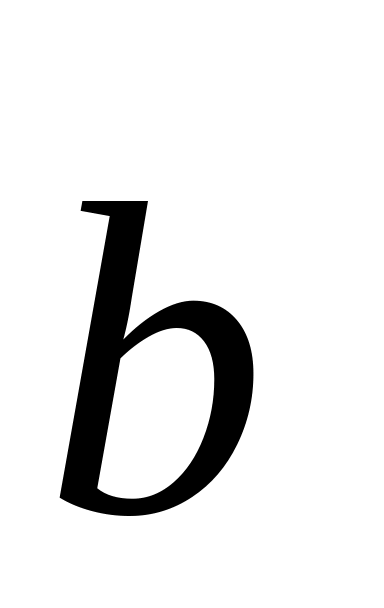
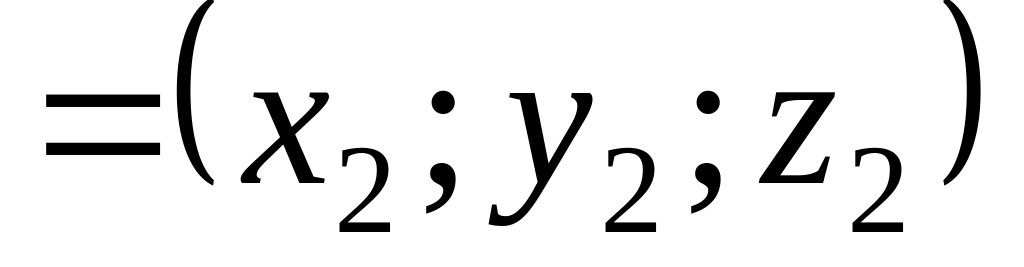визначається
формулою
,
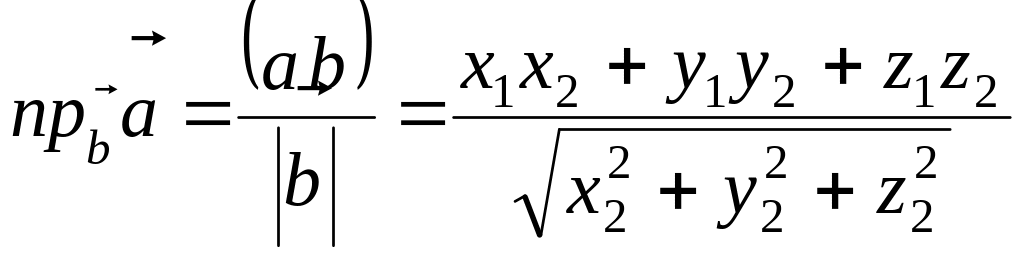тому
.
Оскільки
,
,
,
то
,
;
.
Отже,
.
Об’єм піраміди дорівнює
модуля мішаного добутку векторів
,
.
Знайдемо їх мішаний добуток
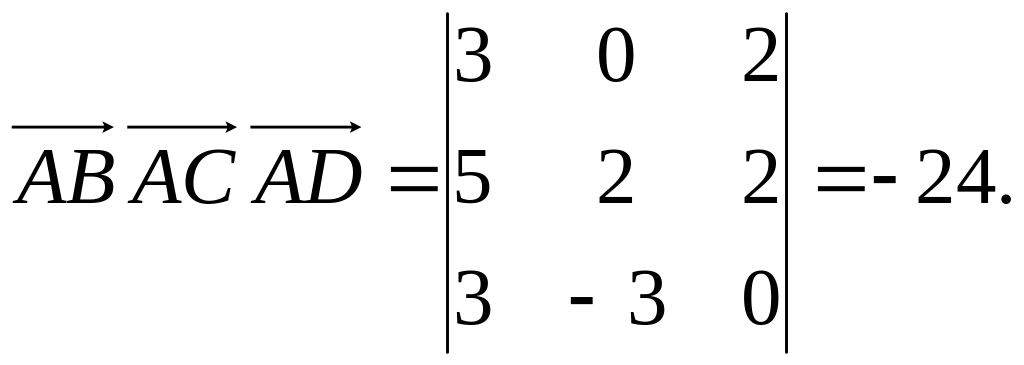
Отже,
(куб. од.).
Запишемо розклад вектора за базисом
,
:
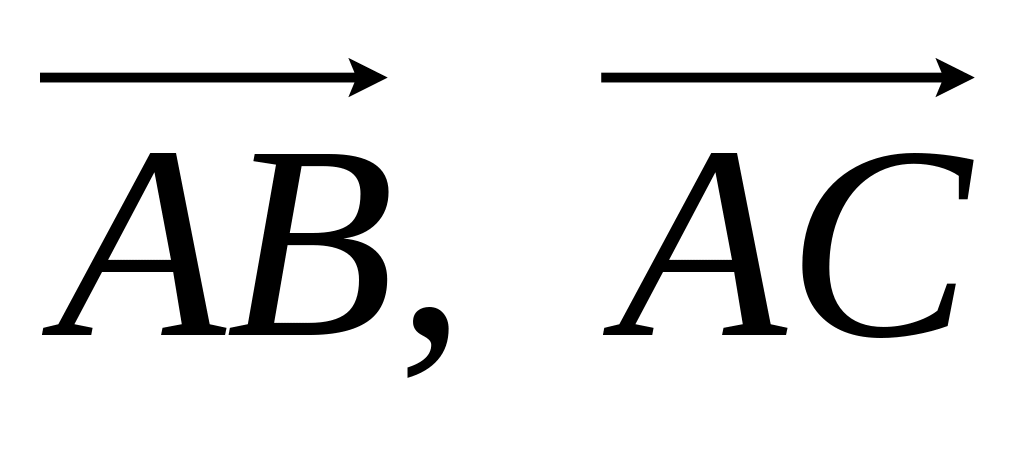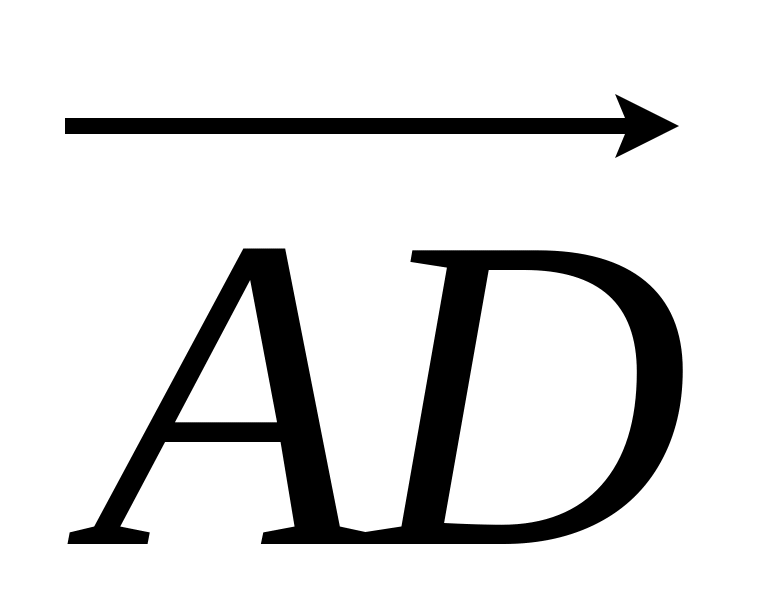, (1)
Оскільки , , , то перепишемо рівність (1) у вигляді
Ця рівність рівносильна системі лінійних рівнянь:
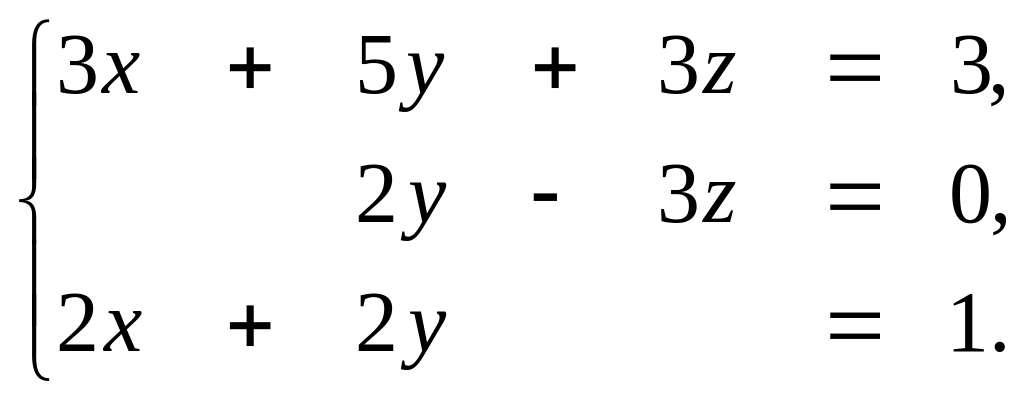
Розв’язавши дану систему будь-яким з методів, знайдемо
Отже,
Задача 2.
Сила
прикладена до точки
.
Визначити:
а) величину
роботи
,
яку виконує сила
при прямолінійному переміщенні
матеріальної точки з початку в кінець
вектора
,
де
,
;
б)
момент цієї сили відносно точки
.
Розв’язання.
а) Робота сили при переміщенні матеріальної точки з початку в кінець вектора дорівнює скалярному добутку сили на вектор переміщення .
Оскільки,
,
то
.
Отже,
.
б) Момент
сили
,
прикладеної до точки
відносно точки
,
визначається векторним добутком
.
Оскільки,
,
то
.
Отже,
.
Розрахункові завдання Завдання 2.1.
Дано координати точок
.
Засобами векторної алгебри знайти:
1) кут між
векторами
та
;
2) площу трикутника ;
3)
;
4) об'єм піраміди ;
5) розкласти
вектор
за базисом із векторів
.
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
26.
.
27.
.
28.
.
29.
.
30.
.
Завдання 2.2.
Сила прикладена до точки . Визначити:
а) величину роботи, яку виконує сила при прямолінійному переміщенні матеріальної точки з початку в кінець вектора, де ,
б) момент цієї сили відносно точки .
1. 
,
,
,
.
2. 
,
,
,
.
3. 
,
,
,
.
4. 
,
,
,
.
5. 
,
,
,
.
6. 
,
,
,
.
7. 
,
,
,
.
8. 
,
,
,
.
9. 
,
,
,
.
10. 
,
,
,
.
11. 
,
,
,
.
12. 
,
,
,
.
13. 
,
,
,
.
14. 
,
,
,
.
15. 
,
,
,
.
16. 
,
,
,
.
17.
,
,
,
.
18. 
,
,
,
.
19. 
,
,
,
.
20. 
,
,
,
.
21. 
,
,
,
.
22. 
,
,
,
.
23. 
,
,
,
.
24. 
,
,
,
.
25. 
,
,
,
.
26. 
,
,
,
.
27. 
,
,
,
.
28. 
,
,
,
.
29. 
,
,
,
.
30. 
,
,
,
.
§ 3. Лінійний простір.
Основні поняття і теореми [5, ст. 40 – 43].