§16. Зведення рівнянь ліній другого порядку до канонічного вигляду.

Основні поняття і теореми [5, ст.228-233].

Зразки розв'язування задач

Задача.

Знайти канонічне рівняння та визначити тип кривої другого порядку

.

Записати відповідні формули перетворення координат. Виконати схематичний рисунок лінії у початковій системі координат.

Розв'язання.

Виписуємо квадратичну форму старших членів

.

Її матриця А має вигляд .

Складаємо і розв'язуємо характеристичне рівняння:

Отже, квадратична форма має такий канонічний вигляд:

.

Знаходимо базис, в якому квадратична форма має канонічний вигляд.

Підставивши у систему

матимемо звідки або , де .

Якщо покладемо , то знайдемо власний вектор . Тоді вектору відповідатиме одиничний вектор .

Підставляючи отримаємо систему розв'язавши яку маємо , . Поклавши , знайдемо власний вектор , звідки .

Отже, і утворюють шуканий ортонормований базис. Перехід до нової системи координат відбувається поворотом осей на кут такий, що і .

Оскільки у разі переходу до базису , координати всіх векторів перетворюються за формулами

, де ,

або , ,

.

Тоді рівняння лінії другого порядку в базисі , матиме вигляд

.

Виділимо повні квадрати в лівій частині останнього рівняння

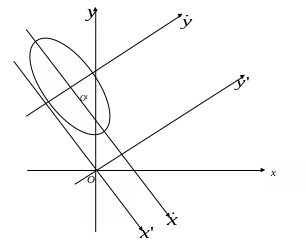
рис. 7

Виконаємо паралельне перенесення координатних осей. Покладемо

.

Новий початок координат в системі матиме координати .

Рівняння лінії в системі координат матиме вигляд або , тобто крива є еліпсом з півосями та .

Початкову систему координат було повернуто на кут , тангенс якого дорівнює . У цій повернутій системі координат центр еліпса розміщено в точці , а осі еліпса паралельні осям координат (рис. 7).

Розрахункові завдання

Завдання 16.

Кожне з наступних рівнянь ліній другого порядку звести до канонічного вигляду. Встановити, які образи вони визначають. Для кожного випадку зобразити вісі початкової системи координат, вісі інших систем координат, які вводяться при розв'язанні, та геометричний образ, який визначається даним рівнянням.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

24. .

25. .

26. .

27. .

28. .

29. .

30. .

§ 17. Зведення загальних рівнянь поверхонь другого порядку до канонічного вигляду.

Основні поняття і теореми [5, ст. 235 – 241].

Зразки розв’язування задач

Задача.

Звести до канонічного вигляду рівняння поверхні другого порядку.

Визначити вид поверхні. Записати відповідні формули перетворення координат.

Розв’язання.

Записуємо квадратичну форму старших членів:

.

Матриця А цієї форми має вигляд

.

Складаємо та розв’язуємо характеристичне рівняння

Квадратична форма F має такий канонічний вигляд:

.

Щоб знайти базис, в якому квадратична форма має такий вигляд, треба знайти власні вектори лінійного оператора, що визначається матрицею А у системі координат Оxyz.

Запишемо систему рівнянь, що визначає шукані власні вектори

1. Підставляючи 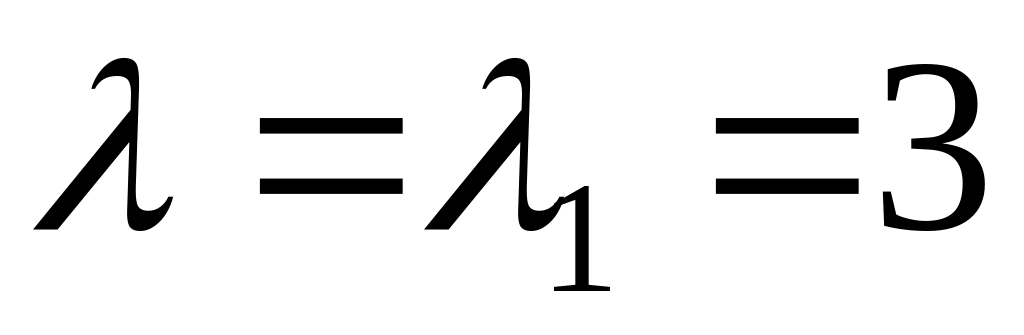, маємо

Звідси, або .

Підставивши , отримаємо власний вектор, що відповідає власному значенню . Тоді одиничний вектор 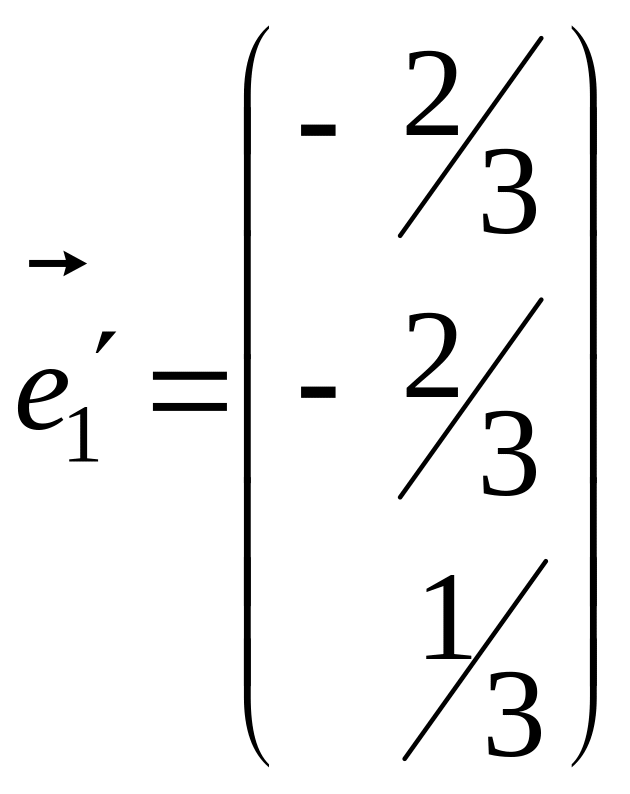співнапрямлений з вектором .

2. Аналогічно для значення 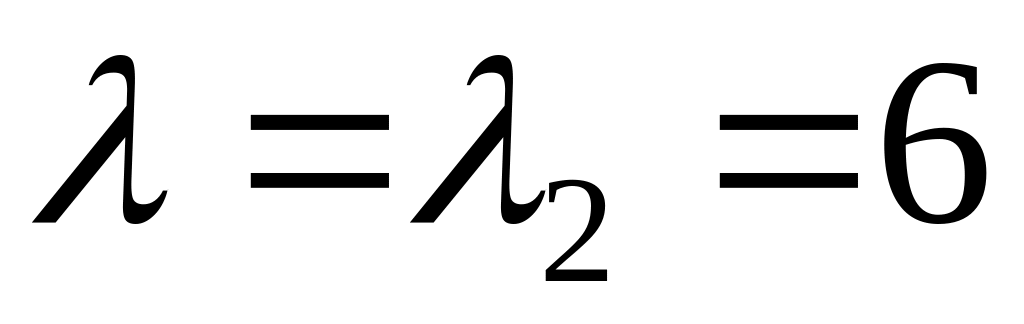, маємо

Звідси, або .

Поклавши , отримаємо власний вектор, що відповідає власному значенню . Тоді одиничний вектор 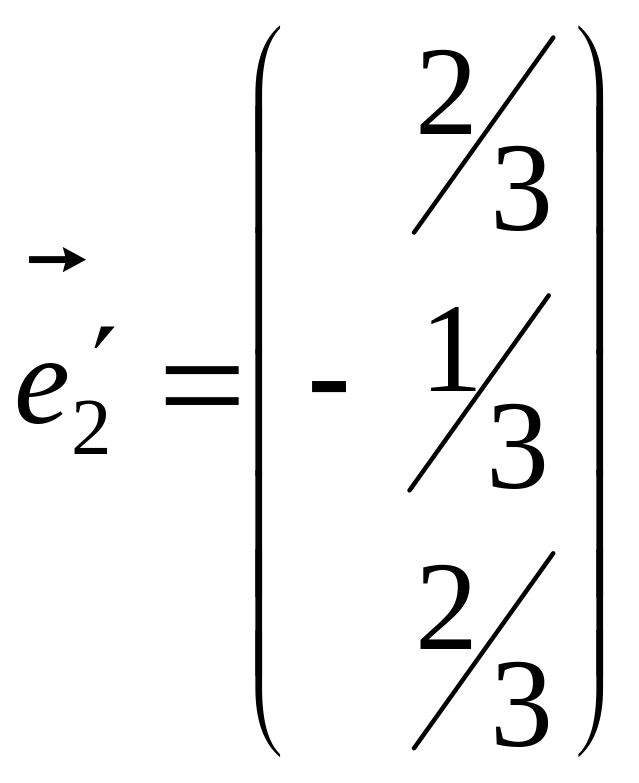співнапрямлений з вектором .

3. Для значення 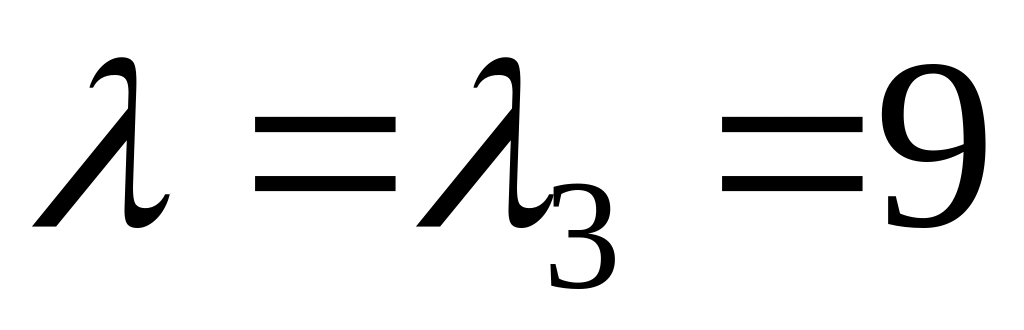, маємо

Звідси, або .

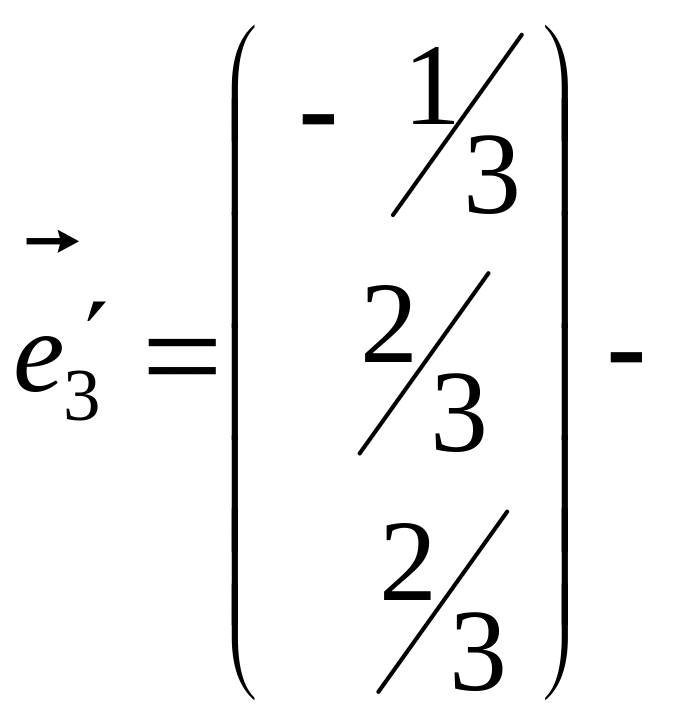Поклавши , дістанемо власний вектор, що відповідає власному значенню . Тоді одиничний вектор співнапрямлений з .

Вектори утворюють шуканий ортонормований базис.

Матриця переходу до базису матиме вигляд

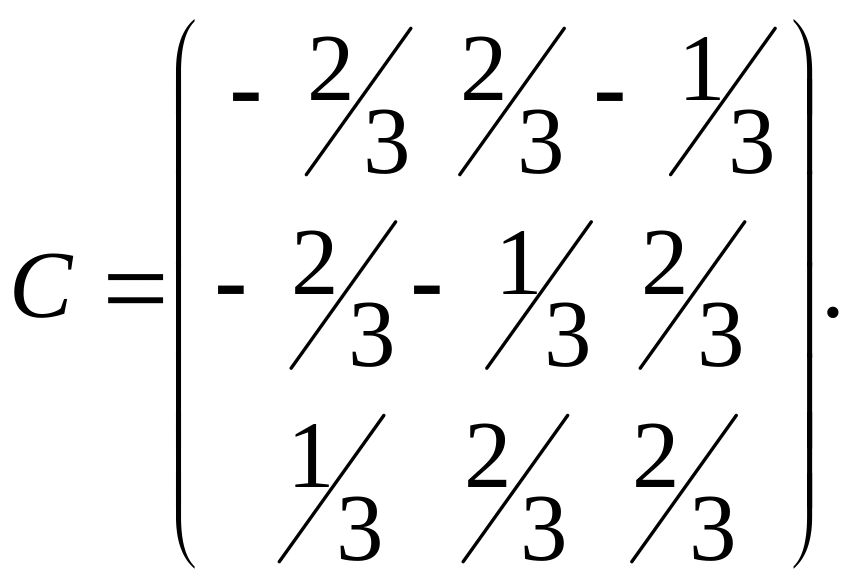
У разі переходу до нового базису координати векторів перетворюються за формулами:

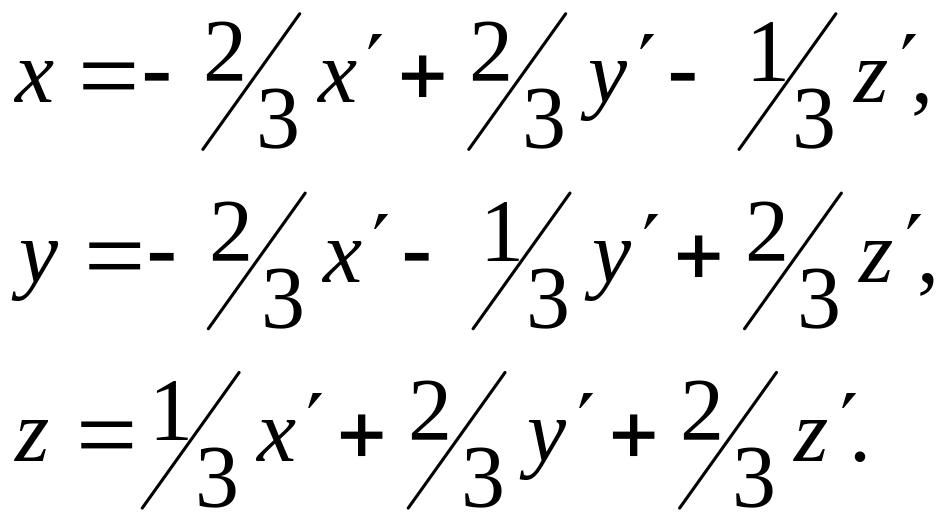
Підставляючи ці вирази для в групу членів першого степеня рівняння поверхні, отрмаємо:

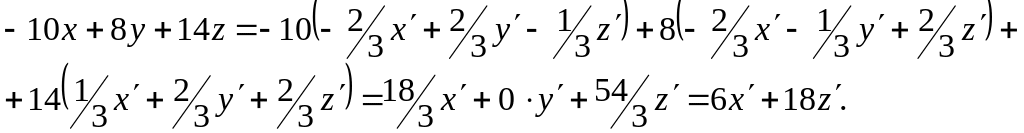
Отже, рівняння даної поверхні в базисі матиме вигляд

або

Звідси

Виконаємо паралельне перенесення координатних осей . Покладемо

.

Новий початок координат в системі Рівняння поверхні в системі координат матиме вигляд

Отже, задана поверхня є еліпсоїдом.