28. Баланс мощности

Представим пассивную электрическую цепь, находящуюся под воздействием источника гармонического напряжения, в форме двухполюсника (см. рис. 1.1). Под воздействием напряжения и_аb= = U_msin  t в цепи протекает ток i = I_msin(  t –   ). Отдаваемая источником в цепь за период Т средняя мощность

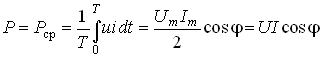. (3.117)

Согласно закону Ома U = ZI или с учетом (3.35) U = RI/cos  . Тогда уравнение (3.117) принимает вид

. (3.118)

Таким образом, средняя за период мощность Р равна мощности, рассеиваемой на резистивном сопротивлении (проводимости) цепи. В этой связи мощность Р носит названиеактивной и измеряется в ваттах (Вт).

Кроме активной мощности Р в цепях гармонического тока используют понятие реактивной мощности

 (3.119)

и комплексной мощности

. (3.120)

Модуль комплексной мощности называется полной мощностью:

. (3.121)

Единица измерения реактивной мощности – вар, а полной – вольт-ампер (В* А).

Мощности P, Q, S можно выразить и в другой форме. Представим S с учетом (3.117) и (3.119) в виде

. (3.122)

Тогда нетрудно видеть, что

 (3.123)

т. е. активная мощность равна реальной части, а реактивная – мнимой части комплексной мощности S. Как следует из формул (3.117) и (3.123):

. (3.124)

Это отношение в энергетике называется коэффициентом мощности (косинусом   ) и является важной характеристикой электрических машин и линий электропередачи. Чем выше cos   , тем меньше потери энергии в линии и выше степень использования электрических машин и аппаратов. Максимальное значение cos    = l, при этом Р = S,

29. Модели электрических цепей с зависимыми источниками

Интегрирующие и дифференцирующие цепи. Интегрирующие и дифференцирующие цепи находят широкое применение в различных устройствах импульсной и вычислительной техники для формирования линейно изменяющихся напряжений и токов, селекции сигналов, линейного преобразования различных импульсов и т. д. Интегрирующая цепь описывается уравнением

, (3.132)

а дифференцирующая – уравнением

, (3.133)

где k₁, k₂ – коэффициенты пропорциональности.

Простейшая интегрирующая и дифференцирующая цепи могут быть реализованы на базе RС-цепочки (рис. 3.33, 3.34). Действительно, если параметры интегрирующей цепочки (рис. 3.33) таковы, что   = RС   t_и, где t_и длительность входного сигнала, то на выходе такой цепи имеем

Рис. 3.33

.

Аналогично, если для дифференцирующей цепочки (рис. 3.34) выполнено условие   = RС   t_и, то

. (3.134)

Однако точность интегрирования и дифференцирования такой пассивной цепи невысока. Поэтому на практике операции (3.132) и (3.133) реализуют с помощью активных цепей с зависимыми источниками, например на базе ОУ.

ARC-цепь второго порядка. На рис. 3.37 изображена активная RC-цепь (ARC-цепь) второго порядка, которая находит широкое применение в качестве типового звена различных устройств: фильтров, корректоров и др. (см.гл.14, 17, 18).

Приняв потенциал узла V₅ = 0 (базисный узел) составим для узлов 3 и 4 уравнения по методу узловых потенциалов (рис. 3.37, б):

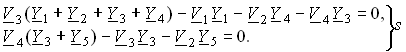 (3.137)

Рис. 3.38

Рис. 3.39

Учитывая, что V₂ = —H_uV₄ и H_u =   (идеальный ОУ) после решения системы уравнений (3.137), получим напряжение на выходе:

. (3.138)

Гиратор. Гиратором называют необратимый четырехполюник (рис. 3.38, а), описываемый уравнениями I₂ = U₁G_г и I₁ = –U₂G_г, где G_г проводимость гиратора.

Условное изображение гиратора показано на рис. 3.38, б. Нагрузим гиратор сопротивлением нагрузки Z₂. Входное сопротивление гиратора

, (3.139)

т. е. обратно сопротивлению нагрузки, поэтому гиратор часто называют инвертором положительного сопротивления. Свойство (3.139) является очень важным, поскольку позволяет имитировать индуктивность с помощью емкости. Действительно, если Z₂ = = l/j  C, то Z₁ = j  L_э, где L_э = C/G_г² – эквивалентная индуктивность. Это свойство гираторов является очень ценным для микроэлектроники, поскольку изготовление индуктивностей по интегральной технологии представляет сложную задачу. Использование же гираторов с малым значением G_г позволяет из небольших емкостей С моделировать большие значения индуктивности L.

Существуют и другие многочисленные применения гиратора: преобразование напряжения и тока, моделирование Т- и П-образных звеньев с катушками индуктивности, трансформаторов, резонансных контуров.