25. Электрические цепи с индуктивными связями

В предыдущих параграфах этой главы рассматривались цепи без учета явления взаимной индукции. В то же время, при протекании тока i₁ в катушке индуктивности с параметром L₁ в окружающем пространстве согласно закону электромагнитной индукции создается магнитный поток Ф₁₁ (рис. 3.17, а). Если какая-либо часть этого потока Ф₁₂ пронизывает витки другой катушки с L₂, то в последней наводится ЭДС взаимной индукции, определяемая законом Максвелла—Фарадея:

, (3.66)

где коэффициент M₁₂ носит название взаимной индуктивности катушек L₁ и L₂. Единица измерения взаимной индуктивности — М генри (Гн).

Знак “–” в уравнении (3.66) определяется согласно правилу Ленца направлением индукционного тока, который имеет такую ориентацию, чтобы создаваемый им магнитный поток препятствовал тому изменению магнитного потока Ф₁₂, которое этот ток вызывает. Напряжение взаимоиндукции на зажимах катушки индуктивности L₂:

. (3.67)

Если напряжение и приложено к катушке индуктивности L₂, то под действием тока i₂ в катушке L₁ также будет наведена ЭДС взаимной индукции:

. (3.68)

В соответствии с принципом взаимности (см. § 1.7) для линейных цепей M₁₂ = M₂₁.

Рассмотренная ниже индуктивная связь носит односторонний характер: ток i₁ вызывает ЭДС взаимоиндукции е_M2, или ток i₂ – ЭДС е_M1. В случае замыкания катушки L₂ на конечное сопротивление R (рис. 3.17, б) в последней под воздействием u_M2, потечет индукционный ток i₂, который в свою очередь, вызовет в первой катушке L₁ ЭДС взаимоиндукции е_M1(3.68). Таким образом, установится двухсторонняя индуктивная связь катушек L₁ и L₂. При этом каждая из катушек L₁ и L₂ будет пронизываться двумя магнитными потоками: самоиндукции, вызванным собственным током, и взаимоиндукции, вызванным током другой катушки. Следовательно, в катушке L₁ индуцируется ЭДС

, (3.69)

а в катушке L₂ ЭДС

. (3.70)

Взаимное направление потоков само- и взаимоиндукции зависит как от направления токов в катушках, так и от их взаимного расположения.

Если катушки включаются таким образом, что потоки само- и взаимоиндукции складываются, то такое включение называется согласным. Если же потоки само- и взаимоиндукции вычитаются, то такое включение принято называть встречным. На рис. 3.17, б показан случай согласного включения.

Степень связи между L₁ и L₂ оценивается коэффициентом связи

. (3.71)

Последовательное соединение. Для согласного включения катушек (см. рис. 3.19, а) в соответствии с ЗНК и уравнениями (3.66) и (3.67) можно записать:

Рис. 3.20

 (3.76)

В комплексной форме уравнение (3.76) согласно § 3.6 запишется в виде

. (3.77)

Обозначим через Z комплексное эквивалентное сопротивление всей цепи при согласном включении катушек

, (3.78)

где

. (3.79)

Тогда уравнение (3.77) можно записать в виде

, (3.80)

отражающем закон Ома для рассматриваемой цепи.

Фазовый сдвиг между током i и приложенным напряжением и

. (3.81)

Параллельное соединение. Для случая согласного включения катушек (рис. 3.21, а) в соответствии с ЗТК и ЗНК можно записать:

 (3.92)

где  .

Решая систему (3.92) относительно I₁ и I₂, получаем

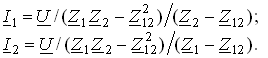 (3.93)

Выражения, стоящие в знаменателях (3.93), имеют смысл эквивалентных комплексных сопротивлений индуктивно связанных ветвей Z_1эc и Z_2эc:

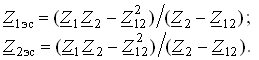 (3.94)

Эти сопротивления складываются из двух составляющих: собственных сопротивлений ветвей Z₁ и Z₂ и сопротивлений, вносимых за счет индуктивных связей Z_1внс и Z_2внс:

. (3.95)

Рис. 3.22

Комплексные вносимые сопротивления Z_1внс и Z_2внс можно определить, решив совместно (3.94) и (3.95):

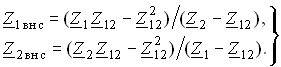 (3.96)

Ток в неразветвленной части цепи I с учетом (3.93)

,

где

. (3.97)

Нетрудно видеть, что в случае отсутствия индуктивной связи (Z₁₂ = Z₂₁ = 0) эквивалентное комплексное сопротивление цепи Z_эс = Z₁Z₂/(Z₁ + Z₂), что соответствует известной формуле параллельного соединения Z₁ и Z₂.

На рис. 3.22, а изображена векторно-топографическая диаграмма для случая согласного включения L₁ и L₂. Аналогичным образом можно получить соответствующие уравнения для встречного включения катушек (см. рис. 3.21, б). При этом необходимо учесть, что в уравнениях перед слагаемыми с Z₁₂ и Z₂₁ необходимо заменить знак на противоположный. Так, уравнения (3.94), (3.96), (3.97) принимают вид

 (3.98)

 (3.99)

. (3.100)